Расчетное исследование процесса кристаллизации при сварке
Содержание
Введение………………………………………………………………………...3
1 Теоретическая часть………………………………………………………….4
2 Расчетное исследование процесса кристаллизации при сварке
плавлением………………………………………………………………………7
3 Расчетное исследование процесса диффузии при сварке плавлением…..12
Заключение…………………………………………………………………….16
Список литературы……………………………………………………………17
Приложение……………………………………………………………………18
Введение
Цель настоящей курсовой работы – получение начальных навыков по исследованию процессов кристаллизации и диффузии при сварке плавлением с помощью численной реализации разработанных ранее ведущими специалистами в области металлургии сварки математических моделей и расчетных схем, получение навыков в анализе полученных результатов расчета.
Исходя из заданной марки стали и ее теплофизических свойств, на основании тепловой схемы точечного сварочного источника нагрева, имеющего конечную скорость прямолинейного движения на полубесконечном теле и конечную тепловую мощность необходимо построить теоретический контур сварочной ванны. На основании модели кристаллизации сварочной ванны М. В. Шаманина – Г. Л. Петрова также следует построить теоретическую ось растущих кристаллитов в сварочной ванне, рассчитать зависимость угла направления касательной в каждой точке теоретической оси кристаллита (угол М. В. Шаманина) и на основании последней построить зависимость скорости кристаллизации сварочной ванны по фронту кристаллизации. На основании заданного режима сварки, толщины свариваемой стальной пластины и теплофизических свойств стали требуется расчет ширины сварного шва (положение границы сплавления), пользуясь схемой линейного мощного быстродвижущегося сварочного источника тепла в бесконечной пластине. Также ведётся расчет, исходя из заданных параметров режима сварки и теплофизических свойств стали, термический цикл точек границы сплавления.
Используя аналитическое решение дифференциального уравнения диффузии (второго уравнения Фика) применительно к одномерному стержню с изначально имеющимся слоем диффундирующего элемента конечной ширины необходимо применить расчет с помощью инженерного метода Г. Л. Петрова диффузионное перераспределение заданного элемента вблизи границы сплавления за эквивалентное время диффузии.
Теоретическая часть
Температурное поле в системе координат, движущейся вместе с источником теплоты, описывается формулой:
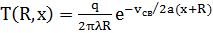, (1)
где q = ƞ∙Iсв∙UД — тепловая мощность дуги, вводимая в свариваемое изделие; Iсв — сварочный ток; UД — напряжение на дуге; ƞ — эффективный КПД;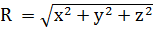 
— расстояние от начала координат до рассматриваемой точки (х, у, z); v — скорость сварки; λ, а — коэффициенты теплопроводности и температуропроводности свариваемого металла соответственно. Функция, задаваемая уравнением (1), имеет осевую симметрию относительно оси х. Поэтому достаточно построить изотерму для интересуемой температуры
Т(х,у)=ТПЛ в плоскости хоу.
Уравнение изотермы плавления в плоскости хоу получается из (1)
при z=0:
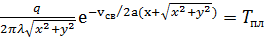(2)
Выражение (2) не удается разрешить явно в виде y=у(х), поэтому построение ветви изотермы Т(х, у)=Тпл следует вести при неявном задании уравнения кривой. Это можно сделать непосредственным численным обсчетом на ЭВМ выражения (2).
Для скорости роста кристаллитов справедливо выражение:
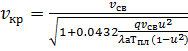(3)
где а=L+xmax, u=y/b – нормированная ордината
Формула М.В.Шаманина:
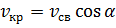(4)
где α – угол между нормалью и направлением движения источника теплоты
Математическая модель процесса одномерной диффузии (одномерной для простоты рассмотрения) может быть представлена уравнением Фика второго рода. Однако это уравнение получено в предположении независимости коэффициента диффузии D от температуры. Такое допущение вполне оправдано для исследования процесса ликвации, так как последняя протекает в узком температурном интервале. В то же время расчет диффузионного перераспределения элементов в условиях термического цикла сварки требует учета зависимости коэффициента диффузии от температуры:
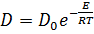(5)
где D0 — частотный множитель, Е — энергия активации, R=8,31 Дж/моль∙К.
Для расчета поля концентрации диффундирующего элемента выбирается одно значение коэффициента диффузии (например D1). Вместо реальной длительности охлаждения объема металла tохл Г. Л. Петров предложил ввести эквивалентное время процесса:
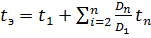(6)
Будем считать, что режим сварки и геометрические размеры сварного изделия с тепловой точки зрения удовлетворительно описываются схемой линейного быстродвижущегося источника в пластине, без учета поверхностной теплоотдачи:
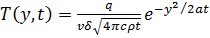(7)
где δ — толщина свариваемой пластины, у — расстояние от оси шва до исследуемой точки A, t — время, прошедшее с момента прохождения источником тепла проекции точки на ось х.
Продифференцировав формулу (7) по t и воспользовавшись необходимым условием максимума, легко найти максимальную температуру Тm и время ее достижения tm по заданной координате исследуемой точки:
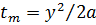(8)
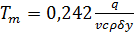(9)
Положив Т=Тm , можно вычислить максимальную ширину сварного шва b:
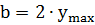(10)
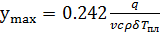(11)
Для расчета поля концентрации С(х, t) воспользуемся готовым аналитическим решением задачи о диффузии элемента из слоя конечной ширины неограниченного образца в изотермических условиях:
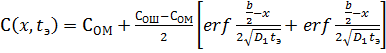(12)
При этом общее время охлаждения tохл можно ограничить остыванием до таких температур, при которых диффузионная подвижность большинства легирующих элементов и примесей (за исключением водорода) в твердых металлах незначительна. Например, можно ограничиться уменьшением коэффициента диффузии в 100 раз:
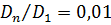(13)
Расчетное исследование процесса кристаллизации при сварке
Плавлением
Задача №1
1. Построить контур сварочной ванны
2. Построить зависимость vкр(х)
3. Построить зависимость α(x)
4. Построить ось кристаллита
Решение:
Исходные данные
Таблица №1
| Iд, А | |
| Uд, В | |
| vсв, м/с | 1,65∙10-3 |
| Сталь | низкоуглеродистая |
| Теплопроводность λ, Вт/(м∙ ͦ С) | 0,153 |
Объемная теплоемкость 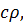 Дж/(м3 ∙ ͦ С) | 1,916 |
| Температуропроводность а, м2/с | 0,08 |
| Температура плавления, ͦ С |
Эффективная тепловая мощность процесса сварки:
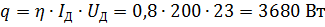
Численным обсчетом на ЭВМ выражения (2) получаем ветвь изотермы Т(х, у) = Тпл:
Таблица №2
| № | X | Xi, см | Yi, см |
| XC | -0,000095 | 0,047798 | |
| X1 | -0,005404 | 0,047502 | |
| X2 | -0,010713 | 0,046603 | |
| X3 | -0,016022 | 0,045066 | |
| X4 | -0,021331 | 0,042821 | |
| X5 | -0,02664 | 0,039749 | |
| X6 | -0,031949 | 0,035636 | |
| X7 | -0,037258 | 0,030058 | |
| X8 | -0,042567 | 0,021926 | |
| XD | -0,048 | ||
| XA | 0,047687 | ||
| XB | 0,04778 |
По данным таблицы №2 строим контур сварочной ванны
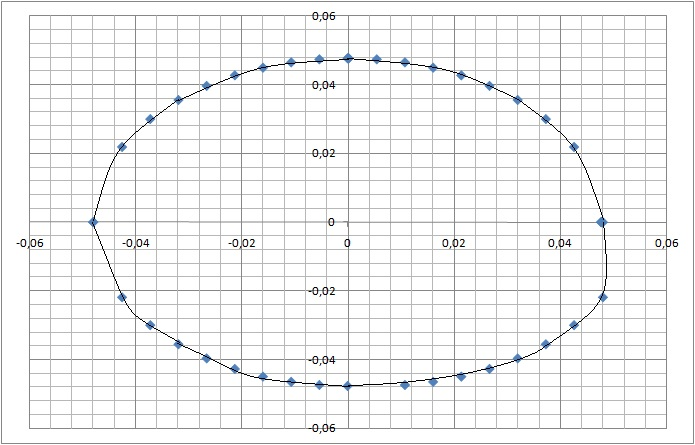
Рис. 1 Контур сварочной ванны
Определим зависимость угла α в функции расстояния от оси шва.
Таблица №3
| Xi, см | α, град. |
| -0,000095 | |
| -0,005404 | |
| -0,010713 | |
| -0,016022 | |
| -0,021331 | |
| -0,02664 | |
| -0,031949 | |
| -0,037258 |
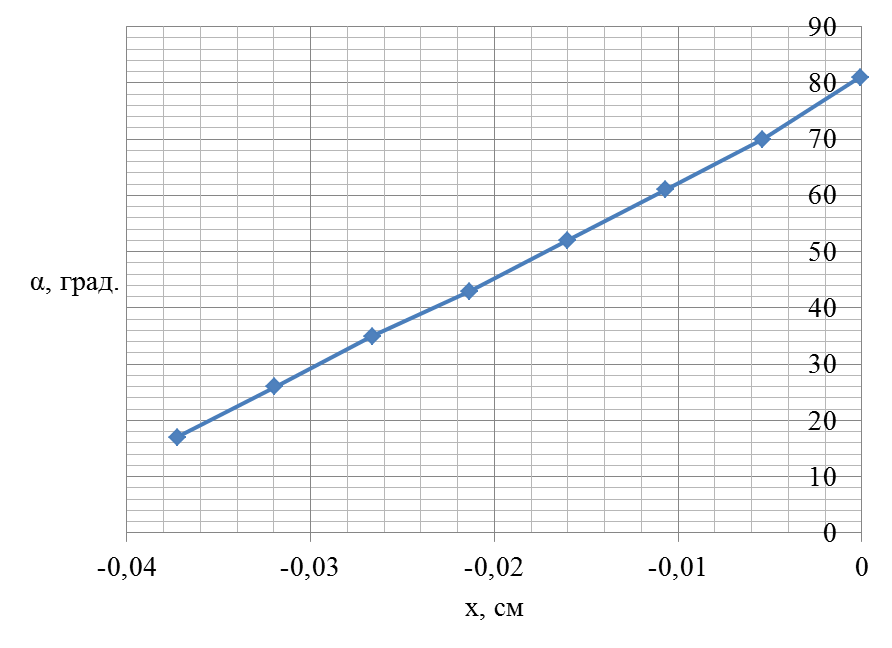
Рис. 2 Зависимость 
(х)
Определим скорость роста кристаллитов Vкр в функции расстояния от оси шва, воспользовавшись формулой (4).
Таблица №4
| Xi, см | Vкр, см/с |
| -0,000095 | 0,000555 |
| -0,005404 | 0,001105 |
| -0,010713 | 0,001665 |
| -0,016022 | 0,002220 |
| -0,021331 | 0,002550 |
| -0,02664 | 0,003330 |
| -0,031949 | 0,003800 |
| -0,037258 | 0,004440 |
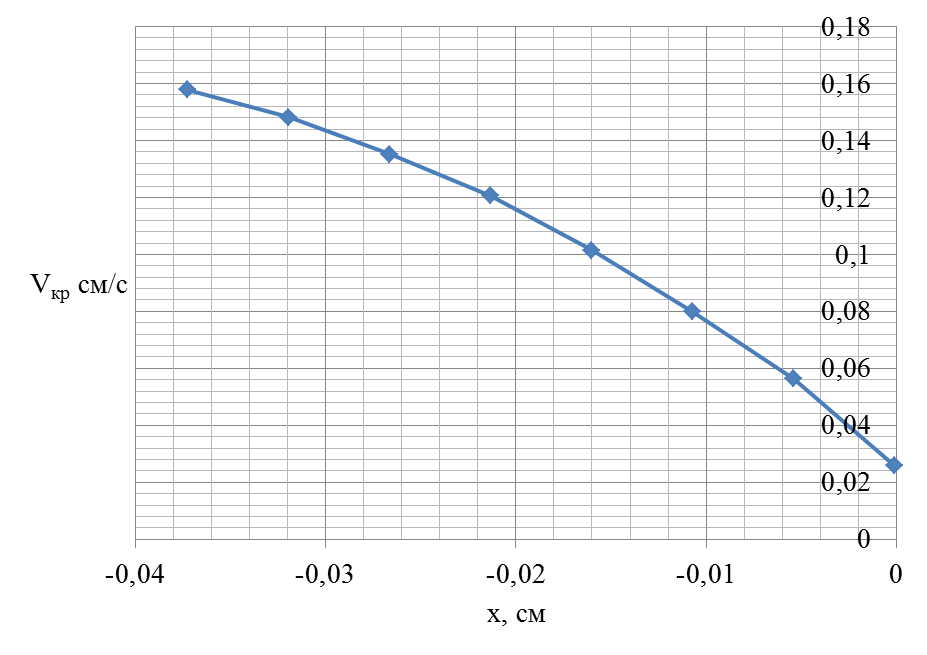
Рис. 3 Зависимость vкр(х)
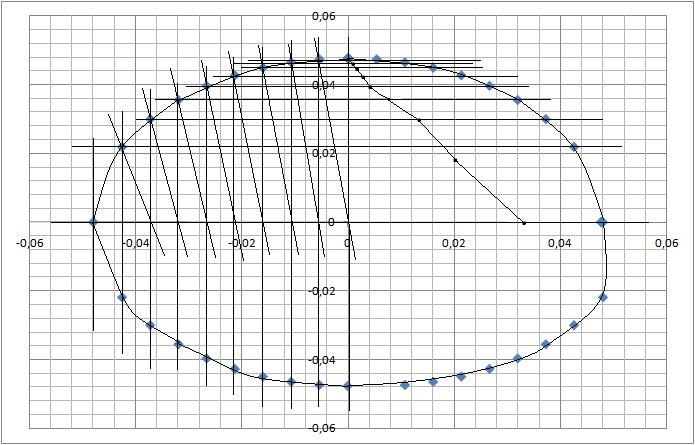
Рис. 4 Ось кристаллита