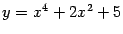Теорема о смешанных производных
Предположим, что:
f (x, y ) определена в некоторой (открытой) области D;
в этой области существуют производные  , а также вторые смешанные производные
, а также вторые смешанные производные 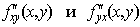 ,
,
эти смешанные производные как функции х и у непрерывны в некоторой точке (х0, у0) области D .
Тогда в этой точке имеет место равенство 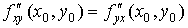 .
.
Доказательство. Рассмотрим выражение
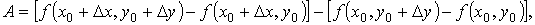
где Δ х и Δ у — любые столь малые числа, что точка M1(x0 + Δ x, y0 + Δ y) находится в указанной области D . Введем вспомогательную функцию
φ (x) = f (x, y0 + Δ y) − f (x, y0);
тогда выражение А можно рассматривать как приращение дифференцируемой на отрезке [х0, х0 + Δ х] функции φ(х) одной переменной х:
A = Δ φ = φ (x0 + Δx) − φ (x0)
Поэтому, применяя к этой разности теорему Лагранжа, запишем
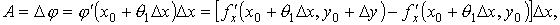
где 0 < θ1 < 1. Выражение в квадратных скобках можно рассматривать как приращение дифференцируемой на отрезке [у0, у0 + Δ у] функции 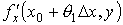 одной переменной у. Применяя еще раз теорему Лагранжа (по переменной у), получаем
одной переменной у. Применяя еще раз теорему Лагранжа (по переменной у), получаем
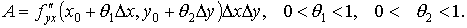 (5)
(5)
С другой стороны, если вести вспомогательную функцию ψ (y) = f (x0 + Δ x, y) − f (x0, y), то, поступая аналогично, получим
A = Δ ψ = ψ (y0 + Δ y) − ψ (y0)
а затем
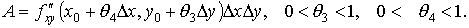 (6)
(6)
Сравнивая (5) и (6), получаем
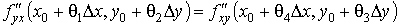 .
.
Переходя теперь в этом равенстве к пределу при Δ х → 0, Δ у → 0 и учитывая непрерывность частных производных
f ''yx(x, y), f ''xy(x, y) в точке М, получим
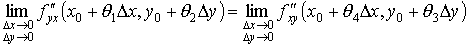
или
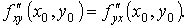
41.Дифференцирование сложной функции z=f(u,v) u=u(t),v=v(t)
Показательно-степенной функцией называется функция вида y = uv, где u = u (x), v = v (x).
Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции .
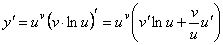
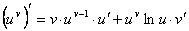
Примеры
1. 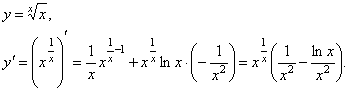
2. 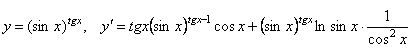 .
.
42.Дифференцирование сложной функции z=f(u,v) u=u(x,y),v=v(x,y)
Дифференцирование функции заданной не явно
Пусть уравнение 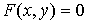 определяет
определяет 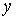 как неявную функцию от х.
как неявную функцию от х.
а) продифференцируем по х обе части уравнения 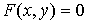 , получим уравнение первой степени относительно
, получим уравнение первой степени относительно 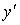 ;
;
б) из полученного уравнения выразим 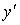 .
.
Пример: 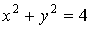 .
.
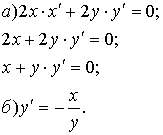
44. 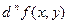
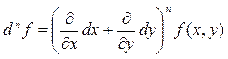
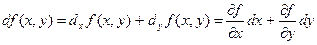
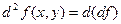
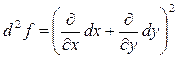
45. Формула Тейлора z=f(x,y)
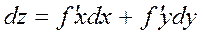
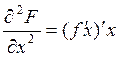
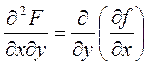
Теорема: 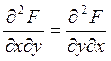
Экстремум. Необходимые условия
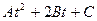 если
если 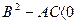 то сохр. знак
то сохр. знак
Если А больше 0 min
Если А больше 0 max
Пусть функция 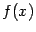 определена в некоторой окрестности
определена в некоторой окрестности 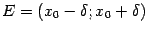 ,
, 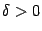 , некоторой точки
, некоторой точки 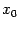 своей области определения. Точка
своей области определения. Точка 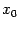 называется точкой локального максимума, если в некоторой такой окрестности
называется точкой локального максимума, если в некоторой такой окрестности 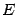 выполняется неравенство
выполняется неравенство 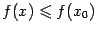 (
( 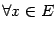 ), и точкой локального минимума, если
), и точкой локального минимума, если 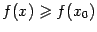
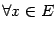 .
.
Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум .
Следующая теорема даёт необходимое условие того, чтобы точка 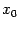 была точкой локального экстремума функции
была точкой локального экстремума функции 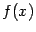 .
.
Если точка 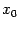 -- это точка локального экстремума функции
-- это точка локального экстремума функции 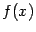 , и существует производная в этой точке
, и существует производная в этой точке 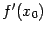 , то
, то 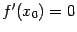 .
.
Доказательство этой теоремы сразу же следует из теоремы Ферма (см. гл. 5).
Утверждение теоремы можно переформулировать так:
если функция 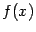 имеет локальный экстремум в точке
имеет локальный экстремум в точке 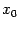 , то либо
, то либо
1) 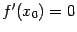 , либо
, либо
2) производная 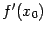 не существует.
не существует.
Точка 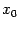 называется критической точкой функции
называется критической точкой функции 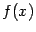 , если
, если 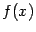 непрерывна в этой точке и либо
непрерывна в этой точке и либо 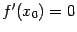 , либо
, либо 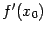 не существует. В первом случае (то есть при
не существует. В первом случае (то есть при 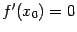 ) точка
) точка 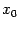 называется также стационарной точкой функции
называется также стационарной точкой функции 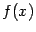 .
.
Итак, локальный экстремум функции 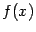 может наблюдаться лишь в одной из критических точек этой функции.
может наблюдаться лишь в одной из критических точек этой функции.
Пример 7.18 Рассмотрим функцию 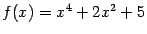 . Её производная существует при всех
. Её производная существует при всех 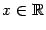 и равна
и равна 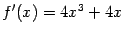 . Следовательно, все критические точки -- стационарные и задаются уравнением
. Следовательно, все критические точки -- стационарные и задаются уравнением 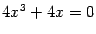 . Это уравнение можно записать в виде
. Это уравнение можно записать в виде 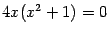 ; оно имеет единственный корень
; оно имеет единственный корень 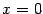 : это единственная стационарная точка. Записав функцию в виде
: это единственная стационарная точка. Записав функцию в виде 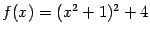 , легко увидеть, что в стационарной точке
, легко увидеть, что в стационарной точке 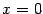 функция имеет минимум, равный
функция имеет минимум, равный 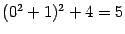 .
.
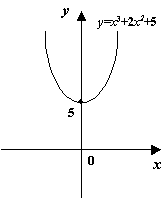
Рис.7.21.График функции