Расчет процессов идеального газа
Все многообразие процессов можно разделить на следующие группы: изохорные, изобарные, изотермические, адиабатные, политропные.
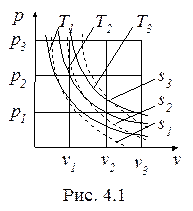 | |||
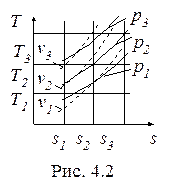 | |||
Цель расчета процесса - определение параметров в начальном и конечном состояниях, а также теплоты и работы процесса. Расчет процессов, как правило, сопровождается графическим представлением их в p-v- и T-s- диаграммах (рис. 4.1, рис. 4.2).
Изобары в T-s- диаграмме располагаются эквидистантно между собой и с увеличением давления смещаются влево; построены на основании уравнения (4.18).
Изохоры в T-s- диаграмме располагаются также эквидистантно между собой и с увеличением объема смещаются вправо; для построения изохор использовалась формула (4.17).
Изотермы в p-v- диаграмме представляют собой симметричные гиперболы, отражающие связь между p и v в изотермическом процессе
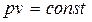 . . | (4.28) |
Адиабаты (изоэнтропы) в p-v- диаграмме - несимметричные гиперболы, отражающие связь между давлением и объемом в адиабатном обратимом процессе,
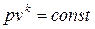 | (4.29) |
располагаются круче изотерм, т.к. показатель адиабаты k >1.
4.2.1. Изобарный процесс
Дано: параметры начального состояния p1, v1, удельный объем конечного состояния v2.
Определить: недостающие термические параметры T1 и T2, работу и теплоту процесса (w, l, q).
Изобарный процесс, построенный на основании исходных данных
(p1, v1, v2), в p-v- и T-s- диаграммах представлен на рис. 4.3 и 4.4.
Из уравнения состояния для точки 1 определяется температура T1:
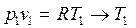 .
.
Сравнение уравнений состояния для точек 1 и 2 при условии
p1 = p2 = p = const
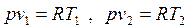
дает связь между v и T в изобарном процессе:
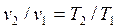 , , | (4.30) |
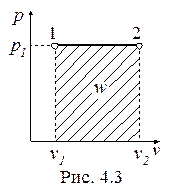 | |||
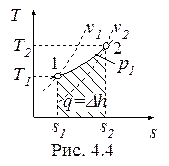 | |||
из которой можно определить искомую температуру T2 .
Формулы для расчета работы и теплоты изобарного процесса легко получить на основании уравнений
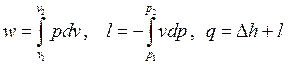 . . |
Отсюда при p = const имеем
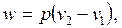 | (4.31) |
 , , | (4.32) |
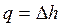 . . | (4.33) |
Работа и теплота изобарного процесса в диаграммах представлены заштрихованными площадями. Работа положительна (w > 0), т.к. v2 > v1, теплота подводится (q > 0), поскольку s2 > s1.
Из T-s- диаграммы следует: изменение энтальпии (Dh) любого процесса, осуществляемого в интервале температур T1 - T2, характеризуется площадью под изобарой в этом интервале температур.
Изохорный процесс
Дано: параметры начального состояния p1, v1, давление конечного состояния p2 (p2 > p1).
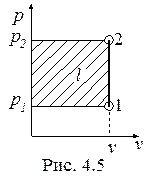 | 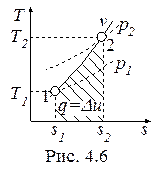 | ||
Определить: недостающие термические параметры T1 и T2, работу и теплоту процесса (w, l, q).
Изохорный процесс, построенный на основании исходных данных (p1, v1, p2) в диаграммах p-v и T-s, представлен на рис. 4.5 и 4.6.
Из уравнения состояния для точки 1 определяется температура T1 = p1.v1/R. Сравнение уравнений состояния для точек 1 и 2 при условии v1 = v2 = v = const (p1.v = RT1, p2.v = RT2) дает связь между давлением и температурой в изохорном процессе:
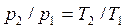 , , | (4.34) |
из которой можно рассчитать температуру T2.
Формулы для расчета работы и теплоты изохорного процесса получены на основании уравнений:
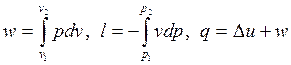 . . |
При v = const получаем
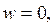 | (4.35) |
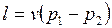 , , | (4.36) |
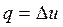 . . | (4.37) |
Работа и теплота изохорного процесса в p-v- и T-s- диаграммах представлена заштрихованными площадями. Работа затрачивается (l < 0), т.к. p2 > p1, теплота подводится (q > 0), поскольку s2 > s1.
Из T-s- диаграммы следует: изменение внутренней энергии ( 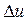 ) любого процесса, осуществляемого в интервале температур T1-T2 , характеризуется площадью под изохорой в этом интервале температур.
) любого процесса, осуществляемого в интервале температур T1-T2 , характеризуется площадью под изохорой в этом интервале температур.
