Общего положения способом 2

Словесная форма	Графическая форма
1. Провести первую вспомогатель­ную плоскость P(Р2).Отметить точки [1222] = [P2ÇΣ2] и [3242] = [P2ÇΔ2]. Построить горизонтальные проекции линий пересечения плоскостей Σ(aIIb) и Δ(cÇd) со вспомогательной плоскостью Р, 1121Ç3141 = M1. Построить фронтальную проекцию М2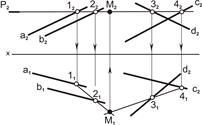
2. Провести вторую вспомогательную плоскость Р`(Р`2). Отметить точки [5262] = [P2ÇΣ2] и [7282] = [P2ÇΔ 2]. Построить горизонтальные проекции линий пересечения плоскостей Σ(aIIb) и Δ(cÇd) со вспомогательной плоскостью Р`(Р2), [5161]Ç [7181] = [N1]. Построить фронтальную проекцию N2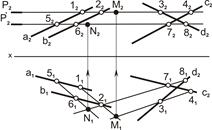

Окончание табл. 5.4

Словесная форма	Графическая форма
3. Соединить точки M1 с N1 и M2 с N2. MN=Σ(aIIb)ÇΔ(cÇd)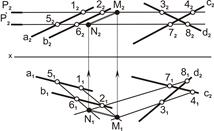

Перпендикулярность двух плоскостей.Две плоскости перпендикулярны, если одна из них проходит через прямую линию, перпендикулярную другой плоскости.

Пример. Через заданную прямую l и точку D, лежащую на этой прямой, построить плоскость P, перпендикулярную данной Σ (Δ АВС).

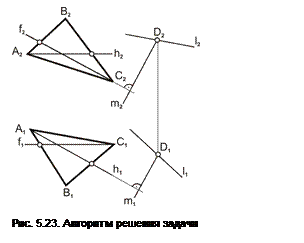Алгоритм решения (рис. 5.23).

1. Построить горизонталь h и фрон­таль f плоскости Σ (Δ АВС).

2. Через точку D провести перпендикуляры к натуральным величинам горизонтали h₁ и фронтали f₂. D₁cm₁ ^ h₁; D₂cm₂ ^ f₂.

Вывод. Так как плоскость P задана (mÇl=D) при этом m^h, где hÌΣ(ΔАВС), то тогда плоскость P перпендикулярна плоскости Σ.

Параллельность плоскостей.Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На рис. 5.24 представлены две плоскости, которые параллельны, так как каждая из плоскостей содержит прямые, которые пересекаются в плоскости и параллельны прямым другой плоскости: Q(ΔABC)II P(DM∩DN)ÞABIIDM и BCIIDN; [A₂B₂]II[D₂M₂] и [B₂C₂]II[D₂N₂]; [A₁B₁]II[D₁M₁] и [B₁C₁]II[D₁M₁] (рис. 5.24).

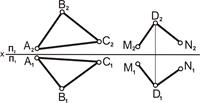
Рис. 5.24. Плоскости параллельные

пример. Через точку D провести плоскость Q, параллельно данной Σ(ΔАВС).

Алгоритм решения (рис. 5.24).

1. Через точку D провести прямую DM, параллельно АВ. Получим [D₁M₁]II(A₁B₁) и [D₂M₂]II(A₂B₂).

2. Через точку D провести прямую DN, параллельно BC. Получим [D₁N₁]II(B₁C₁) и [D₂N₂]II(B₂C₂).

Вывод. Так как плоскость Ω задана (DMÇDN = D), а плоскость Σ задана (ΔАВС), где ABÇBC=B, при этом DMllAB и DNllBC, то плоскости Q и Σ параллельны.

Выводы по теме

1. Плоскость в пространстве может быть задана:

– проекциями трёх точек, не лежащих на одной прямой линии;

– проекциями прямой линии и точки, не лежащей на этой прямой;

– проекциями двух параллельных прямых;

– проекциями плоской фигуры;

– следами плоскости.

2. Плоскость в пространстве занимает: общее положение, не перпендикулярное ни одной плоскости проекций и частное положение, перпендикулярное, либо параллельное плоскости проекций. Различают проецирующие плоскости и плоскости уровня.

3. Прямая линия может принадлежать плоскости, быть параллельна плоскости, пересекать плоскость.

Среди прямых, принадлежащих плоскости, выделяют главные линии плоскости – прямые, принадлежащие плоскости, параллельные плоскостям проекций, – это горизонталь, фронталь, профильную прямую, линию наибольшего ската.

Прямая перпендикулярна плоскости, если ее горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна к фронтальной проекции фронтали плоскости.

4. Две плоскости могут быть: параллельны и пересекаться. Линией пересечения двух плоскостей является прямая линия. Проекции прямой линии пересечения двух плоскостей общего положения определяются проекциями двух точек, принадлежащих одновременно обеим плоскостям.

Ключевые слова

· Плоскость

· Плоскость общего положения

· Плоскость уровня (горизонтальная, фронтальная, профильная)

· Проецирующая плоскость

· Условие принадлежности прямой плоскости

· Главные линии плоскости (горизонталь, фронталь, профильная прямая, линия наибольшего наклона)

· Условие перпендикулярности прямой и плоскости

· Условие параллельности двух плоскостей

· Условие перпендикулярности плоскостей