Процедура вычеркивания дублирующих и заведомо невыгодных стратегий

Если игра не имеет седловой точки, то нахождение решения это довольно трудоемкая задача, особенно при больших значениях и . Иногда эту задачу удается упростить, если предварительно уменьшить число стратегий путем вычеркивания дублирующих и заведомо невыгодных стратегий. Процедура вычеркивания дублирующих и заведомо невыгодных стратегий всегда должна предшествовать решению игры.

Задача № 6.4.

Пусть игра задана платежной матрицей:

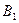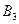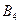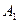	7	6	5	4	2
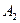	5	4	3	2	3
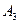	5	6	6	3	5
	5	4	3	2	3

Упростить платежную матрицу.

Решение.

Стратегия в точности повторяет (дублирует) стратегию 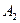, поэтому любую из этих двух стратегий можно вычеркнуть. Вычеркнем . Стратегия 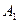является заведомо более выгодной по сравнению со стратегией 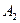, поэтому стратегию 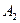также вычеркнем. После преобразований у игрока осталось две стратегии: 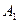, 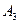. Для игрока стратегия 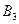заведомо более выгодна, чем стратегия 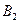(как бы ни повел себя игрок , проигрыш игрока будет не больше, если он воспользуется стратегией 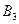, вместо 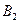). Вычеркнем стратегию 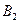. Сравнивая проигрыш игрока при применении стратегии 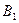с проигрышем при применении стратегии , придем к выводу о необходимости вычеркнуть стратегию ._. 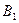Сравнивая проигрыш игрока при применении стратегии 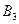с проигрышем при применении стратегии 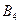, приходим к выводу о необходимости вычеркнуть стратегию 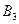. В результате преобразований получим матрицу .

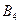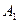	4	2
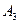	3	5

Решение игровых задач размерности

Наиболее простыми случаями конечных игр, которые всегда можно решить элементарными способами, является игра . Рассмотрим игру с платежной матрицей

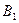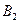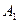	а11	а12
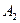	а21	а22

Возможны два случая: 1) игра имеет седловую точку; 2) у игры нет седловой точки. В первом случае решение очевидно: это пара стратегий, пересекающихся в седловой точке. Заметим, что в игре наличие седловой точки всегда соответствует существованию заведомо невыгодных стратегий, которые должны быть вычеркнуты при предварительном анализе.

Предположим, что седловой точки нет и, следовательно, нижняя цена игры не равна верхней цене игры: . Требуется найти оптимальную смешанную стратегию игрока :

.

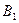В игре обе стратегии противника являются активными, иначе игра имела бы решение в области чистых стратегий (седловую точку). Значит, если мы придерживаемся своей оптимальной стратегии , то противник в любых пропорциях может смешивать свои чистые стратегии и 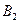, не изменяя среднего выигрыша.

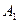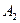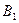Предположим, что игрок воспользовался своей оптимальной стратегией , смешивая стратегии и в оптимальных пропорциях, а игрок при этомкаждый раз использует стратегию . В этом случае средний выигрыш игрока будет равен , в то же время он будет равен цене игры 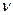. Аналогично, пусть игрок воспользуется своей оптимальной стратегией , а игрок при этомкаждый раз будет использовать стратегию 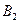. В этом случае средний выигрыш игрока будет равен и в то же время он будет равен цене игры .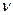

Принимая во внимание, что , составим систему уравнений:

(6.1)

Решив систему (6.1), найдем искомые частоты , и чистую цену игры .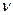

Если цена игры известна, то для определения оптимальной стратегии противника , зная что , достаточно составить одно уравнение. Предположим, что игрок воспользовался своей оптимальной стратегией, а игрок воспользовался стратегией 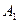. Выигрыш игрока в этом случае будет равен .

Задача № 6.5.

Найдем решение игры , заданной платежной матрицей (см. задачу № 6.4):

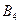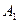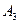Решение.

Игра не имеет седловой точки: , 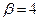. Следовательно, решение должно лежать в области смешанных стратегий:

, .

Найдем неизвестные частоты применения активных стратегий для обоих игроков, а также чистую цену игры. Составим системы уравнений:

.

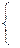
Решив системы, получим , , , .

Следовательно, если игрок воспользуется своей оптимальной стратегией , то как бы ни повел себя игрок , выигрыш равный чистой цене игры будет всегда у игрока . Если игрок воспользуется своей оптимальной стратегией , то как бы ни повел себя игрок , увеличить свой выигрыш, равный чистой цене игры он не сможет.