Определение независимости случайных величин

Пусть задана система (X, Y). Мы скажем, что величины X и Y независимы, если независимы события X Î А и Y Î В, где А и В – любые два отрезка [a1, a2] и [b1, b2].

Иными словами выполняется равенство

P(X Î A, Y Î B) = P(X Î A)× P(Y Î B).

13.* Математические операции над дискретными случайными величинами. Примеры.

Если случайная величина может принимать конечное или счетное множество значений, то она называется дискретной (дискретно распределенной).

1. «Сдвиг». Пусть имеется дискретная СВ Х, принимающая в зависимости от результата тесты те либо другие случайные значения. Ежели к каждому из этих значений прибавить одно и то же число, к примеру, А, то в итоге получим новейшую СВ - Х + А, принимающую значения ( 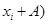, При всем этом:

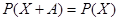, т.е. с теми же вероятностями, что и СВ Х.

Х	х1	…	хn
Р	р1	…	рn

Х + А	х1 + А	…	хn + А
Р	р1	…	pn

2. Определение. Произведением дискретной СВ на число с именуется дискретная СВ сХ, принимающая значения 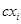с вероятностями .

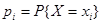3. «Возведение в степень».

Определение. Квадратом (соответственно – m-степенью) дискретной СВ Х именуется дискретная СВ, принимающая значения 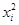(соответственно - 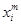) с вероятностями 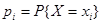. Обозначение – Х² (соответственно – X^m).

Построение таблицы значений СВ Х² несколько труднее. Разглядим определенный пример.

Задачка. СВ Х задана таблицей распределения. Найти закон распределения СВ Х².

Х	-1
Р	0,2	0,3	0,4	0,1

Решение. Действуем аналогичным методом для вычисления Х², т.е. заменяем все значения х_i значениями их квадратов - х_i², и получаем:

Х2
Р	0,2	0,3	0,4	0,1

В первой строке имеются совпадающие значения. Потому следует объединить их в одну варианту, сложив надлежащие вероятности.

Х2
Р	0,6	0,3	0,1

Таблицу распределения хоть какой СВ У = f(x) для хоть какой функции f можно выстроить аналогично. Она строится в два шага. Поначалу рассчитываются элементы вспомогательной таблицы.

СВ	f(x1)	f(x2)	…	f(xn)
Р	p1	p2	…	pn

Потом совпадающие значения f(x_i) = f(x_j) для различных значений x_i и x_j (ежели такие имеются) объединяются в одно, а надлежащие вероятности складываются.

4. Определение. Суммой дискретной СВ Х, принимающей значения 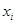с вероятностями 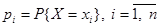и СВ Y, принимающей значения 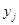с вероятностями 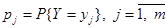именуется дискретная СВ Z = Х + Y, принимающая значения 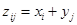с вероятностями 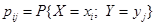для всех указанных значений i и j.

5. Определение. Разностью дискретной СВ Х, принимающей значения 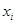с вероятностями 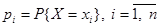и СВ Y, принимающей значения 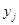с вероятностями 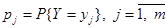именуется дискретная СВ Z = Х - Y, принимающая значения 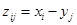с вероятностями 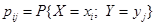для всех указанных значений i и j.

6. Определение. Произведением дискретной СВ Х, принимающей значения 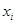с вероятностями 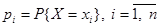и СВ Y, принимающей значения 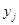с вероятностями 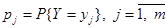именуется дискретная СВ Z = Х·Y, принимающая значения 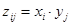с вероятностями 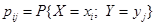для всех указанных значений i и j.