Группа 3. аксиомы конгруэнтности

Группы аксиом 1-3 позволяют доказать основные свойства отношения конгруэнтности между геометрическими фигурами, определить понятие движения в геометрии и установить признаки конгруэнтности геометрических фигур. Первая аксиома этой группы содержит два требования, а четвертая три.

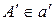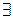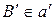13. Пусть дан отрезок АВ а также прямая а^/ и точка . точка с заданной стороны относительно точки 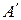такая, что отрезок АВ конгруэнтен отрезку 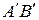(обозначим это АВ=АВ), требуется также, чтобы АВ=ВА.

14.

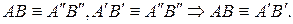
15. Пусть АВ и ВС – отрезки на прямой 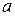, АВ 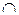ВС=В, тогда
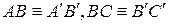и 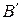лежит между 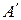и .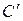

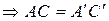16. Пусть Ð 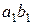есть угол с вершиной О. Для любой точки 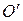и любого выходящего из нее луча 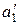можно построить в заданной плоскости, инцидентной 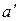, по любую сторону от 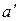один и только один, второй луч 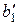такой, что Ð .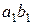

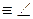
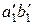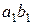
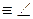
Требуется также, чтобы Ð 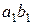(угол конгруэнтен самому себе) и Ð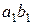

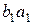
17. Пусть даны два треугольника АВС и 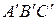таких, что 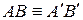, , 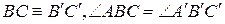тогда .

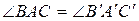На основании аксиом конгруэнтности вводятся понятия прямого угла, смежных и вертикальных конгруэнтных углов, операции сравнения углов и отрезков. Отрезок АВ больше отрезка СD, обозначается АВ>СD, если при совмещении точек А и С и откладывании точек В и D по одну сторону от точки А на некоторой прямой, точка D будет лежать между
А и С.

В этой группе аксиом доказываются три признака конгруэнтности треугольников, свойства равнобедренных и равносторонних треугольников и т.д. Справедлива также теорема о внешнем угле треугольника в слабом варианте (известная еще Евклиду).

Теорема (о внешнем угле треугольника).

Внешний угол треугольника больше любого не смежного с ним угла треугольника.

Аксиомы 13-17 позволяют ввести операцию движения в геометрии.

Определение движения.

Взаимно-однозначное соответствие точек плоскости 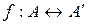называется движением, если соответствующим парам точек 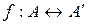, 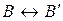соответствуют конгруэнтные отрезки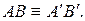

Замечание 1.

В этой группе вместо аксиом 13-17 можно аксиоматически задать движение и некоторые его свойства. Тогда аксиомы 13-17 будут являться теоремами, которые доказываются на основании аксиом движения.

Вывод 1.

Аксиомы 1-17 первых трех групп позволяют построить геометрию, в которой на прямой существует последовательность примыкающих друг к другу конгруэнтных отрезков, пронумерованных натуральным рядом. В этой геометрии есть конгруэнтные и правильные фигуры, определено понятие движения, совмещающего конгруэнтные фигуры и т. д.

Но в этой геометрии еще нет понятия параллельного переноса, не определено соответствие между действительными числами и точками прямой. Отсутствуют понятия длины отрезка, площади и объема геометрических фигур. Следовательно, в этой геометрии еще нет понятия расстояния и понятий «близости» и «непрерывности», связанных со свойствами расстояния между точками. Хотя абстрактные понятия близости и непрерывности уже можно вести на языке шаровых окрестностей.

Действительно, шаром В (O, OА) с центром в точке О и радиусом ОА назовем все точки М такие, что ОМ<ОА. Далее, шар В(О,ОА₁) Ì B(О,ОА₂), если ОА₁<ОА₂, таким образом, множество окрестностей точки О есть множество всех шаров В(О, ОР_к ), kÎN, где Р_к- любая точка пространства. Определим последовательность точек М_кÎВ(О,ОР_к), kÎN условиями а) и b):

а) ОР₁>ОР₂>…>ОР_к>…, что означает, что мы имеем последовательность вложенных шаров В(О,ОР₁)ÉВ(О,ОР₂)É…É В(О,ОР_к) É…;

b) М_кÏВ_к+1 "кÎN , что означает, что каждая последующая точка выбирается в следующем вложенном шаре.

Вывод 2.

Используя лишь аксиомы I-III групп мы не сможем установить существование предела у последовательности М_1, М_{2, …,} М_к, … , а в случае существования мы не сможем доказать его единственность.