Распределительная матрица задачи №6.01
| Станки | Ткани | Фонд времени 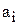 , ч , ч | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 2 ( 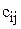 ) ( ) ( 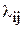 ) 24 ) 24 | ||||
| А2 | |||||
| А3 | |||||
Объем выпуска 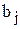 , м , м |
ЦФ имеет смысл себестоимости выпуска запланированного количества ткани всех видов
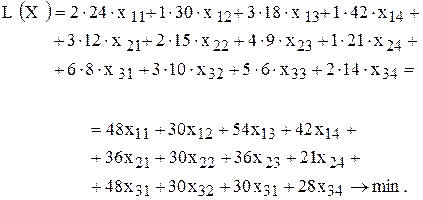
Ограничения имеют вид
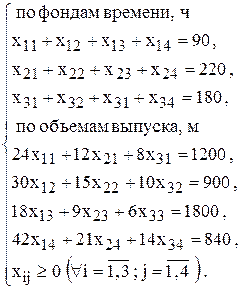
Преобразуем РЗ в ТЗ, т.е. представим исходную задачу в виде, когда ткани производит только один станок – базовый и все параметры задачи согласуем с его характеристиками. В качестве базового можно выбирать любой из станков. Мы выберем станок с максимальной производительностью, т.е. 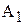 . По формуле (6.2) определим производительности станков
. По формуле (6.2) определим производительности станков 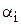 , нормированные относительно производительности базового станка:
, нормированные относительно производительности базового станка:
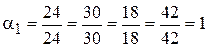 ;
;
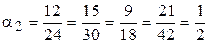 ;
;
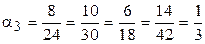 .
.
Таким образом, базовый станок работает в два раза быстрей второго станка и в три раза быстрей третьего.
Пересчитаем фонды времени станков по формуле (6.3):
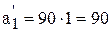 [ч];
[ч]; 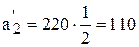 [ч];
[ч]; 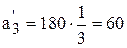 [ч].
[ч].
Из этих величин следует, что тот объем работ, который второй станок выполняет за свой фонд времени 220 ч базовый станок сможет выполнить за 110 ч. Аналогично объем работ, который третий станок выполняет за 180 ч базовый выполнит за 60 ч.
Пересчитаем плановое задание по формуле (6.4):
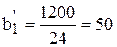 [ч];
[ч]; 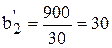 [ч];
[ч]; 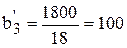 [ч];
[ч]; 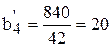 [ч].
[ч].
Отсюда следует, что план выпуска первого вида ткани базовый станок выполнит за 50 ч, второго вида – за 30 ч и т.д.
Пересчет себестоимостей производим по формуле (6.5), например:
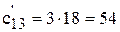 [руб./ч];
[руб./ч]; 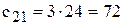 [руб./ч];
[руб./ч]; 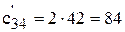 [руб./ч].
[руб./ч].
В полученной ТЗ условие баланса (4.2) не выполняется, т.к. суммарный фонд времени станков больше, чем это необходимо для выполнения плана по выпуску всех тканей (260 ч > 200 ч). Введем фиктивный столбец 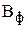 и запишем все пересчитанные параметры РЗ в транспортную матрицу (см. табл.6.3). Фиктивные тарифы для упрощения приравняем к нулю.
и запишем все пересчитанные параметры РЗ в транспортную матрицу (см. табл.6.3). Фиктивные тарифы для упрощения приравняем к нулю.
Таблица 6.3
Транспортная матрица задачи №6.01
| Станки | Ткани | Фонд времени 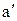 , ч , ч | ||||
| В1 | В2 | В3 | В4 | ВФ | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
Объем выпуска 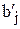 , ч , ч |
Для упрощения вместо оптимального решения рассмотрим опорный план 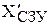 , найденный методом северо-западного угла.
, найденный методом северо-западного угла.
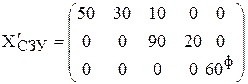 [ч].
[ч].
Преобразуем опорный план ТЗ 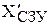 в опорный план РЗ
в опорный план РЗ 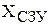 согласно (6.6)
согласно (6.6)
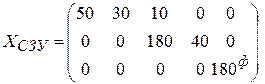 [ч].
[ч].
Таким образом, первый станок должен 50 ч производить ткань первого вида, 30 ч – ткань второго вида и 10 ч – ткань третьего вида. Второй станок должен 180 ч производить ткань третьего вида и 40 ч – ткань четвертого вида. А третий станок будет простаивать, не выпуская ткань вообще, т.к. согласно решению, его загрузка находится в фиктивном столбце ( 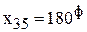 ).
).
Определим, сколько метров ткани каждого вида должны произвести станки по формуле (6.7)
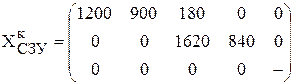 [м].
[м].
Определим общую себестоимость производства по формуле (6.1), используя вычисленные значения элементов матрицы 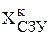
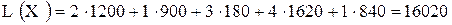 (руб.).
(руб.).
Варианты задач для самостоятельного решения
Задача №6.1
Решите РЗ, исходные данные которой приведены в табл.6.4.
Таблица 6.4
