Применение методов МММ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное агентство по образованию

Санкт-Петербургский государственный университет сервиса и экономики

Кафедра "Прикладная математика и эконометрика"

В.К. Каракадько

Е.А. Яковлева

Экономико-математические методы оптимизации финансов, денежного обращения

Практикум
для студентов специальностей
080105.65 (060400) «Финансы и кредит»,

080107.65 (3512) «Налоги и налогообложение»

Санкт-Петербург
2011

Одобрено на заседании кафедры «Прикладная математика и эконометрика», протокол № 8 от 22.02.2011 г.

Одобрено и рекомендовано к изданию Учебно-методическим советом СПбГУСЭ, протокол № от г.

Каракадько В.К., Яковлева Е.А. Экономико-математические методы оптимизации финансов, денежного обращения. Практикум – СПб.: Изд-во СПбГУСЭ, 2011. – 35 с.

Практикум подготовлен в соответствии с требованиями Государственного образовательного стандарта ВПО для специальностей 080105.65 (060400) «Финансы и кредит», 080107.65 (3512) «Налоги и налогообложение» и в соответствии с рабочей программой по дисциплине «Экономико-математические методы оптимизации финансов, денежного обращения».

Предназначено в первую очередь для студентов, обучающихся по специальностям 080105.65 (060400) «Финансы и кредит», 080107.65 (3512) «Налоги и налогообложение» и может быть полезно для студентов экономических специальностей, изучающих математику.

Научный редактор: канд. физ.-мат. наук, проф. С.И. Никитин

Рецензент: д-р физ.-мат. наук, проф. Санкт-Петербургского государственного университета сервиса и экономики А.И. Шерстюк;

Ó Санкт-Петербургский государственный университет
сервиса и экономики
2011 г.

Содержание.

1. Предисловие…………………………………………………………….4

2. Тематическое содержание дисциплины математические методы и модели в финансовом и денежном обращении……………………….4

3. Применение методов МММ для решения задач………………………4

3.1. Построение модели для оптимального формирования пакета ценных бумаг……………………………………………………………4

3.2. Применение графического метода для решения математической модели задачи о формировании портфеля из двух ценных бумаг…...7

3.3. Применение метода Гомори для решения математической модели задачи о формировании портфеля из двух и более ценных бумаг….12

4. Решение задач финансового и денежного обращения с помощью моделей финансовых вычислений……………………………………18

4.1. Модели наращения………………………………………………19

4.2. Модели дисконтирования……………………………………….25

5. Решение задач по определению стоимости акций……………………30

5.1. Модель оценки цены по ожидаемой доходности акции………30

5.2. Модель расчета цены на основе постоянного роста дивидендов акции…………………………………………………………………….31

5.3. Модифицированная модель оценки цены акции………………32

Литература………………………………………………………………36

І. Предисловие.

Дисциплина МММ оптимизации финансово-денежного обращения является продолжением раздела математики «Исследование операций в экономике».

В данной работе рассмотрены некоторые вопросы финансовой деятельности, и разобраны примеры задач, решаемых с помощью математических методов.

- Применение методов МММ для решения задач.

- Решение задач финансового и денежного обращения с помощью моделей финансовых вычислений.

- Решение задач по определению стоимости акций.

Приведены и решены задачи по указанным разделам.

Для каждого раздела представлены аналогичные задачи для самостоятельной работы студентов.

Чтобы приступить к решению задач, приведенных в настоящем практикумуме, студенту рекомендуется: изучить литературу, рекомендованную на странице 31, подробно разобрать решенные примеры по теме, и только после этого приступить к самостоятельному решению заданий по данной теме. Для каждой задачи даны 10 вариантов.

2. Тематическое содержание дисциплины.

Понятие сущности наращения и дисконтирования, общая модель наращения и дисконтирования. Модели простых и сложных процентов. Доходность финансовой операции. Прямые и обратные финансовые задачи.. Модели математического и банковского дисконтирования. Дисконтирование по простой и сложной ставке. Учет векселей.

Виды финансовых рисков. Вероятностный характер риска. Акции. Модели оценки цены акции: по ожидаемой доходности, модель на основе постоянного роста дивидендов. Модифицированная модель оценки стоимости акции (с учетом реинвестирования). Применение методов математического программирования для формирования модели оптимального портфеля ценных бумаг.

Применение методов МММ.

3.1.Построение модели для оптимального формирования пакета ценных бумаг.

Один из способов выгодного вложения средств, с целью получения прибыли является вложение средств в ценные бумаги. Целью любого инвестора, имеющего свободные средства, является определение направления, доходности инвестиций, а так же уровень риска. Так же важно своевременно определить, когда следует изменить направление вложений, то есть выставить на продажу имеющиеся акции с целью покупки других.

При решении подобных задач нужно учитывать значительное количество факторов: размер имеющихся средств, рыночную цену, срок, доходность и ожидаемую доходность ценных бумаг, риск финансовых вложений, прогнозируемую стоимость ценных бумаг.

Оценка эффективности вложений и определение ожидаемой прибыли может быть сформирована и получена методами математического программирования. Простейшие задачи решаются методами линейного целочисленного программирования – графическим для двух видов ценных бумаг и симплексным методом для двух и более видом.

Построим математическую модель для определения оптимального состава пакета из двух видов ценных бумаг, с целью получения максимальной прибыли.

Целевая функция определяет прибыль, которую будут приносить купленные ценные бумаги

,

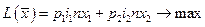где , 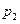- рыночная цена акций первого и второго вида, 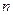- срок операции в годах, 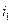, 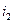- ожидаемые доходности акции каждого вида, 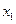, 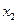- количество акций каждого вида соответственно.

В систему ограничений будет входить бюджетное ограничение, определяемое средствами S, которыми располагает инвестор:

+ .

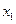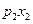
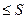Ограничим количество покупаемых акций 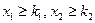. Исходя из экономического смысл задачи, наложим естественные ограничения: 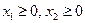, и дополнительные ограничения 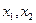- целые.

Полученная математическая модель будет иметь вид:

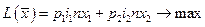
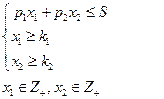
Получили простую задачу линейного программирования, записанную в стандартной форме. Она легко решается графическим методом. Серьезный недостаток этой модели - произвольное определение ограничений на количество покупаемых ценных бумаг.

Составим более сложную модель для определения оптимального состава портфеля ценных бумаг. Для этого введем новые параметры.

Первый из них – это мера риска. Финансовый риск выражает неопределенность исхода финансовой операции, он носит вероятностный характер. Обычно за меру риска выбирается среднее квадратическое отклонение от ожидаемой доходности. В общем случае доходность ценных бумаг, как и исход любой финансовой операции, является случайной величиной. Инвестор может только предполагать, какую доходность 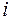будет иметь ценная бумага, поэтому среднее квадратическое отклонение доходности 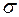от ее ожидаемого значения логично принять за меру риска.

Второй параметр К – это коэффициент склонности инвестора к риску, который является субъективной личностной характеристикой инвестора. При увеличении К и постоянстве остальных условий инвестор может выбирать акции с большим риском. По данным психологов, склонность человека к риску изменяется от 0 до 40. Если этот показатель составляет 30 и более, то это рискующий человек, значения от 11 до 29 показывают среднюю склонность к риску, менее 11 – характеризуют человека, как осмотрительного.

Учитывая, что инвестор будет стараться ограничивать риск, то для каждого вида акций, ограничение величины риска 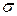имеет вид. (см. лит. [3]).

(*)

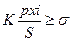Где:

p – цена одной акции,

х – количество приобретенных акций данного вида,

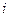- доходность акции («сложная» годовая процентная ставка наращения),

S – сумма денег, предназначенная для покупки акций обоих видов,

К – коэффициент, определяющий склонность инвестора к риску,

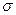- риск акции (среднее квадратическое отклонение доходности ).

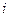Более удобно ограничения по риску (*) представить в виде

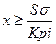
Таким образом, ограничение на количество приобретаемых ценных бумаг получит экономическое обоснование. Усложненная математическая модель примет вид:

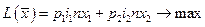
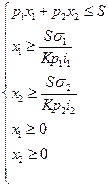
Данная задача так же может решаться графическим методом.

Покажем, как можно решить эту задачу методом Гомори. Тем более, что если число переменных 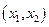- не две, а более, то задачу определения оптимального пакета ценных бумаг можно решить только с использованием симплексных методов. Использование любого симплексного метода предполагает, что система ограничений записана в канонической форме. В канонической форме все ограничения задачи заданы уравнениями и значения переменных неотрицательны. Для перехода к канонической форме в левую часть каждого неравенства системы ограничений вводятся балансовые переменные. Если знак неравенства 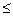, то балансовая переменная вводится в левую часть неравенства со знаком плюс, если 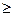- то со знаком минус.

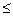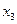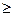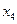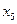Приведем задачу, рассмотренную выше, к канонической форме. В системе ограничений в первом неравенстве знак , поэтому балансовая переменная вводится со знаком плюс; во втором и третьем ограничении знаки неравенств , поэтому балансовые переменные и вводятся со знаками минус.

Математическая модель задачи примет вид:

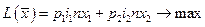
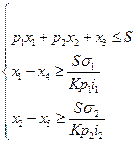
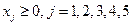
3.2.Применение графического метода для решения математической модели задачи о формировании портфеля из двух ценных бумаг.

На формирование портфеля из двух видов акций инвестор планирует потратить 5000 рублей. Коэффициент склонности к риску у инвестора одинаков по акциям и равен 5. Характеристики акций заданы в таблице:

Тип акции	Ожидаемая доходность i %	Среднее квадратическое отклонение от доходности 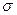, %	Рыночная цена акции p, руб.
I
II

Срок, на который покупаются акции, 1 год. Найти оптимальный состав портфеля и ожидаемый доход за год.

Решение.

Обозначим 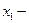количество приобретаемых акций I вида, 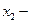количество приобретаемых акций II вида. Тогда бюджетное ограничение, связанное с имеющейся суммой S = 5000 руб, можно представить в виде: .

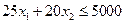Ограничения по риску для каждого вида акций:

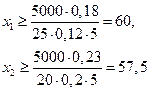
или .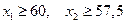

Добавим дополнительные условия, исходя из экономического и финансового смысла задачи: 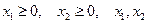- целые.

Составим целевую функцию :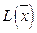

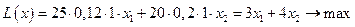. Таким образом математическая модель задачи принимает вид:

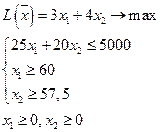
Построим область допустимых решений. Границы этой области определяются уравнениями, соответствующими неравенствам из системы ограничений 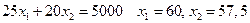и дополнительными условиями .

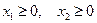Сторона многоугольника допустимых решений, образованная границей 1-го неравенства, задается уравнением 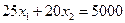. Для нахождения полуплоскости, соответствующей неравенству 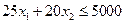, выберем контрольную точку, например, с координатами (0, 0). Подставляем в неравенство, получаем 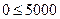. Так как неравенство выполняется, то искомой является полуплоскость, находящаяся ниже этой прямой и содержащая контрольную точку. Аналогично строим прямые и выбираем полуплоскости для остальных неравенств. Часть плоскости, удовлетворяющая всем неравенствам – область допустимых решений, это область, ограниченная .

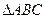Область допустимых решений – это 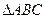(см. рис.).

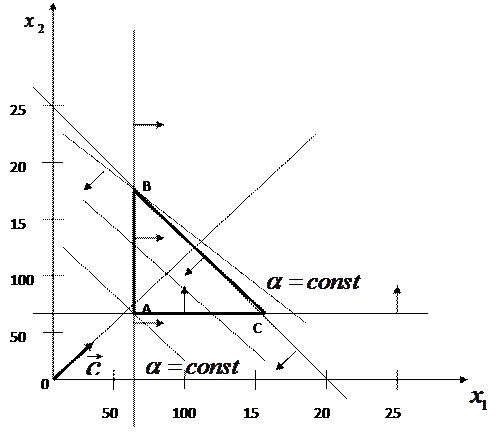
Построим вектор наибольшего роста целевой функции. 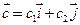, где 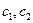- координаты вектора, перпендикулярного линиям уровня целевой функции 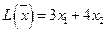. Это вектор .

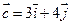Линии уровня, перпендикулярные 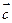, определяются соотношением 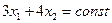. Будем перемещать линию уровня по направлению вектора 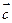. Последней общей точкой области линии уровня и допустимых решений является точка В, образованная пересечением прямых 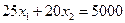и х=60. Именно в этой точке целевая функция достигает максимального значения. Решая систему уравнений 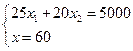, определяем координаты точки В: 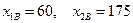. Вычисляем значение целевой функции в этой точке: .

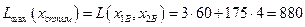Таким образом для получения максимального ожидаемого дохода 880 рублей, инвестору следует купить 60 акций первого вида и 175 акций второго вида.