Основы теории плавания
Для проведения кружковой работы по судомоделированию учителю технологии необходимо знать основы теории плавания, уметь определять остойчивость судна в надводном положении и принимать меры по обеспечению необходимой остойчивости и безопасности плавания на воде. Основой теории плавания является закон Архимеда, установленный им 250 лет до н.э.
Из курса физики известно, что закон Архимеда формулируется следующим образом: на тело, погруженное в жидкость, действует выталкивающая сила равная по величине и обратная по направлению силе тяжести жидкости, вытесненной этим телом.
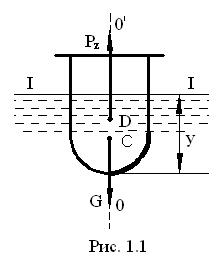
В надводном положении на плавающее тело по оси OZ действуют две силы (рис.1.1).Это сила тяжести тела G и выталкивающая архимедова сила Pz.
 | Способность тела плавать, т.е. держаться на поверхности при заданной нагрузке, называется плавучестью и определяется по неравенству (3.1): 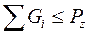 , (3.1) где , (3.1) где 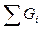 - суммарная сила тяжести судна и дополнительной загрузки. Отметим, что при подводном - суммарная сила тяжести судна и дополнительной загрузки. Отметим, что при подводном |
плавании, т.е. в погруженном состоянии 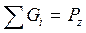 . К основным понятиям теории плавания относятся следующие:
. К основным понятиям теории плавания относятся следующие:
- плоскость плавания (I-I) - пересекающая тело плоскость свободной поверхности жидкости;
- ватерлиния – линия пересечения поверхности тела и плоскости плавания;
- осадка (y) – глубина погружения низшей точки тела. Наибольшая допустимая осадка судна отмечается на нём красной ватерлинией;
- водоизмещение – вес воды, вытесненный судном. Водоизмещение судна при полной нагрузке является его основной технической характеристикой;
- центр водоизмещения (точ. D, рис. 1.1) – центр тяжести водоизмещения, через который проходит линия действия выталкивающей архимедовой силы;
- ось плавания (О О ' ) – линия проходящая через центр тяжести С и центр водоизмещения D при равновесии тела.
Для сохранения равновесия ось плавления должна быть вертикальна. Если на плавающее судно в поперечном направлении действует внешняя сила, например сила давления ветра, то судно накренится, ось плавания повернётся относительно точки С и возникнет крутящий момент Мк, вращающий судно относительно продольной оси против часовой стрелки (рис.1.2) ↓.
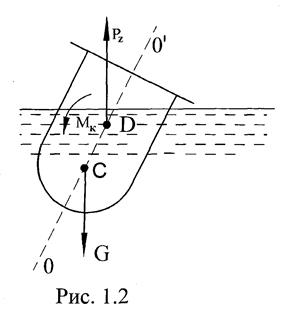 | После прекращения действия внешней силы судно может вернуться в исходное положение, или опрокинуться в зависимости от его остойчивости. Остойчивость - способность плавающего тела, выведенного из равновесия, возвращаться в исходное положение после прекращения действия сил вызвавших крен. |
Остойчивость плавающего тела зависит от взаимного положения точек С и D. Если центр тяжести С находится ниже центра водоизмещения D, то при надводном плавании тело всегда остойчиво, так как возникающий при крене крутящий момент Мк всегда направлен в сторону противоположную крену.
Если точка С находится выше точки D (рис.1.3), то плавающее тело 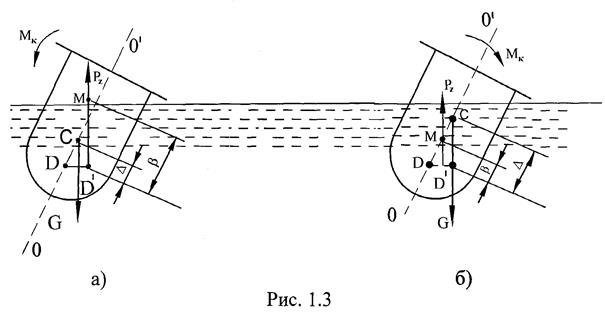
может быть остойчивым и неостойчивым. Рассмотрим эти случаи подробнее.
При крене центр водоизмещения D смещается по горизонтали в сторону крена, так как один борт судна вытесняет больший объём воды, чем другой.
Тогда линия действия выталкивающей архимедовой силы Pz пройдёт через новый центр водоизмещения D' и пересечётся с осью плавания ОО' в точке M, называемой метацентром. Для формулирования условия остойчивости обозначаем отрезок
M D1 = b,аСD1 =∆ ,
где b - метацентрический радиус;
∆- эксцентриситет.
Условие остойчивости: тело остойчиво, если его метацентрический радиус больше эксцентриситета, т.е. b > ∆.
Графическая интерпретация условия остойчивости представлена на рис. 1.3, из которого видно, что в случае а) b > ∆ и возникший крутящий момент направлен в сторону противоположную крену, а в случае б) имеем: b < ∆ и момент Мк вращает тело в сторону крена, т.е. тело не остойчиво.
При решении задач на остойчивость необходимо использовать справочные данные о значениях моментов инерции твёрдых тел относительно горизонтальной оси. При малых углах крена метацентрический радиус b определяется по формуле (2.8):
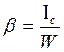 , (3.8)
, (3.8)
где Ic - центральный момент инерции площади ватерлинии относительно оси поворота;
W – объём погруженной части тела.
Центральный момент инерции Ic - определяется по одной из формул таблицы Приложения 2 в зависимости от формы поперечного сечения плавающего тела.
** Почему металлическое судно не тонет?...
** Способы повышения остойчивости….
Основы гидродинамики
Гидродинамика изучает законы движения жидкостей и взаимодействия их с соприкасающимися телами [4]. В теоретической гидродинамике принята струйная модель потока жидкости, где элементарная струйка представляет собой часть потока бесконечно малого сечения. Причём, скорость частиц жидкости в пределах сечения струйки одинакова. Для описания геометрии потока используются следующие кинематические элементы:
-живое сечение;
- смоченный периметр;
- гидравлический радиус.
Живое сечение ω - это поперечное сечение потока, нормальное ко всем линиям тока его пересекающим (рис. 4.1).
Смоченный периметр c - линия, по которой жидкость соприкасается с поверхностями русла (рис. 4.2).
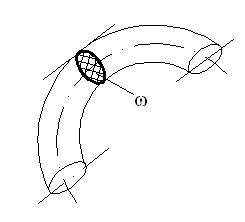 Рис. 4.1 Рис. 4.1 | 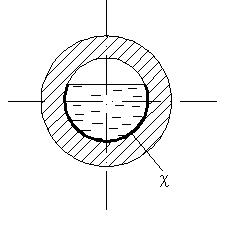 Рис. 4.2 Рис. 4.2 |
Отметим, что при напорном движении жидкости в трубе жидкость занимает весь внутренний объём и смоченный периметр равен геометрическому параметру трубы.
Гидравлический радиус R – это отношение площади живого сечения к смоченному периметру, т.е.
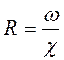 , м (4.1)
, м (4.1)
При напорном движении в круглой трубе 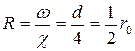 , где
, где 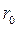 - геометрический радиус трубы, d – внутренний диаметр.
- геометрический радиус трубы, d – внутренний диаметр.
** Гидравлический радиус круглой трубы…..
Основными гидравлическими характеристиками потока являются
расход жидкости, средняя скорость и давление.
Расход – это количество жидкости, протекающее через живое сечение потока в единицу времени.
Количество жидкости может измеряться в различных физических величинах и в соответствии с ними расход может быть объёмный, массовый и весовой.
Рассмотрим математические выражения различных видов расходов для элементарных струек:
- объёмный расход dQ, м3/с:
dQ = 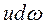 , (4.2)
, (4.2) 
где u - скорость жидкости в струйке.
- массовый расход dM, кг/с:
dM = 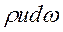 , (4.3)
, (4.3)
где 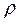 - плотность жидкости.
- плотность жидкости.
- весовой расход dG, н/с:
dG = 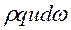 (4.4)
(4.4)
В практических расчётах потоков жидкостей, часто используется объёмный расход Q , выражение для которого получим после интегрирования (4.2):
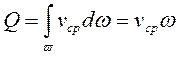 , м3/с (4.5)
, м3/с (4.5)
где 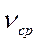 - средняя скорость потока.
- средняя скорость потока.
Одним из основных уравнений гидродинамики является уравнение неразрывности потока, которое связывает между собой скорости потока и площади живых сечений при условии постоянства расхода в различных сечениях [5]. Для несжимаемой жидкости это уравнение имеет следующий вид:
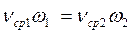 , (4.6)
, (4.6)
Уравнение (3.6) принято представлять в виде пропорции:
νср1 / vcр2= ω2 /ω1 (4.7)
Из выражения (3.7) можно сделать вывод: скорости потока обратно пропорциональны площадям живых сечений.
** Вывод уравнения неразрывности потока ….
Это уравнение часто используется при расчётах трубопроводов, состоящих из труб различных диаметров.
В случае движения сжимаемой жидкости (газа) при переходе от одного сечения к другому её удельный вес 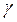 изменяется, тогда уравнение (3.6) преобразуется в (3.8):
изменяется, тогда уравнение (3.6) преобразуется в (3.8):
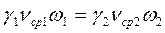 (4.8)
(4.8)
Уравнение Бернулли
Движение жидкости в потоке сопровождается взаимным превращением различных видов механической энергии. Например, при сужении потока его скорость, а следовательно и кинетическая энергия увеличивается, а давление и потенциальная энергия уменьшаются. Уравнение, описываю-
щее эти превращения, называется уравнением Бернулли и для потока идеальной жидкости имеет следующий вид:

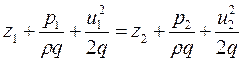 , м, (5.1)
, м, (5.1)
где z – высота положения;
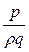 - пьезометрическая высота;
- пьезометрическая высота;
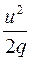 - скоростной напор.
- скоростной напор.
Так как все слагаемые уравнения (3.9) имеют линейную размерность, то их можно изобразить графически (рис.5.1), что даёт наглядное представление об изменении различных видов удельных энергий при переходе от одного сечения к другому.
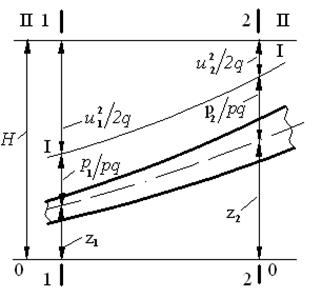
Рис. 5.1: 00 – плоскость сравнения;
I-I – пьезометрическая линия;
II-II – напорная плоскость;
Н – полный гидродинамический напор.
Анализ графиков рис. 5.1 показывает, что напорная плоскость II – II проходит параллельно плоскости сравнения, а полный гидродинамический напор Н = const. Из проведённого анализа следует, что при движении идеальной жидкости её полная механическая энергия не изменяется.
Однако, широко используемые в технике жидкости, такие как масло, вода и др., по своим свойствам близки к реальным жидкостям, в которых при движении между частицами возникают силы внутреннего трения. При движении такой жидкости её удельная энергия уменьшается, так как она частично расходуется на преодоление силы трения. С учётом потерь напора на трение уравнение Бернулли (5.1) для потока реальной жидкости будет иметь следующий вид:
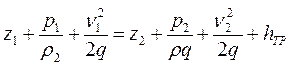 , (5.2)
, (5.2)
где hTP – потери напора на трение, м.
Потери напора на трение численно равны гидравлическим сопротивлениям, которые в зависимости от природы их проявления подразделяются на два вида:
- сопротивления по длине;
- местные сопротивления.
Сопротивления по длине проявляются по всей длине участков труда, а местные сопротивления обусловлены различными конструктивными элементами, создающими препятствия движению жидкости (кран, вентиль, поворот потока и т.п.)
На рис. 3.4 показан участок трубопровода, на котором обозначены коэффициенты сопротивлений местных и по длине. В соответствии с видами гидравлических сопротивлений потери напора hTP также подразделяются на потери напора по длине hL и местные потери hM [6] .
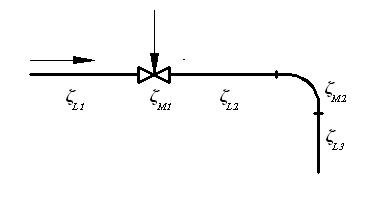
Рис. 2.4: 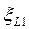 ,
, 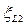 ,
, 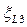 - коэффициенты сопротивления по длине;
- коэффициенты сопротивления по длине;
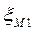 ,
, 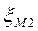 - коэффициенты местных сопротивлений
- коэффициенты местных сопротивлений
В гидравлических расчётах используется принцип наложения потерь:
hTP = 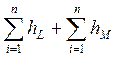 (5.3)
(5.3)
На практике определение hTP осуществляется по уравнению Бернулли, или по формуле Байсбаха. При равномерном движении жидкости (v1 = v2) и горизонтальном трубопроводе (z1 = z2) из уравнения Бернулли получим:
hTP = 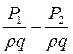 (5.4)
(5.4)
Отметим, что при небольших напорах давления P1 и P2 в уравнении (5.1) можно измерить пьезометром.
В проектных расчётах hTP обычно определяют по формуле Байсбаха:
hTP = 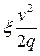 (5.5)
(5.5)
Формулы Байсбаха для определения потерь напора местных и по длине отличаются одна от другой только индексами при h и 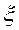 :
:
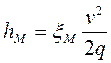 , (5.6)
, (5.6)
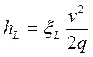 (5.7)
(5.7)
Местный коэффициент сопротивления 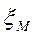 является технической характеристикой данного сопротивления и определяется по справочным таблицам.
является технической характеристикой данного сопротивления и определяется по справочным таблицам.
Коэффициент сопротивления по длине ξL в формуле (2.15) зависит от коэффициента сопротивления трения λ (коэффициента Дарси). Эта зависимость устанавливается формулой (5.8):
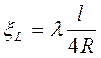 , (5.8)
, (5.8)
где l - длина участка трубопровода, м;
R - гидравлический радиус трубы, м.
Для трубопровода круглого сечения с учётом 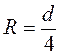 формула (5.8) будет иметь следующий вид:
формула (5.8) будет иметь следующий вид:
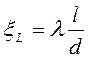 , (5.9)
, (5.9)
где d – диаметр трубы участка трубопровода.
Подставив (5.9) в выражение (5.7) получим общую формулу для определения потерь напора на преодоление сопротивления по длине в круглой трубе:
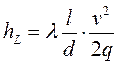 (5.10)
(5.10)
Расчёт значений коэффициента сопротивления трения 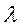 осуществляется по эмпирическим формулам в зависимости от вида движения жидкости, определяемого числа Рейнольдса Re:
осуществляется по эмпирическим формулам в зависимости от вида движения жидкости, определяемого числа Рейнольдса Re:
Re = 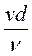 , (5.11)
, (5.11)
где 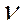 - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.
Из курса физики известно, что переход ламинарного движения в турбулентное в круглой трубе осуществляется при Reкр = 2320.
Если Re< 2320, то режим движения ламинарный и коэффициент сопротивления трения 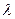 определяется по формуле (5.12):
определяется по формуле (5.12):
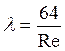 (5.12)
(5.12)
При Re > 2320 используется формула (5.13):
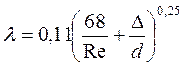 , (5.13)
, (5.13)
где 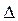 - шероховатость стенки трубы, м.
- шероховатость стенки трубы, м.
Уравнение Бернулли для потока реальной жидкости (5.2) используется при расчётах гидравлических систем перекачки. Так, если в системе имеется насос, то требуемый напор насоса Нн можно определить из уравнения (5.2), записав его в разностном виде:
Нн = 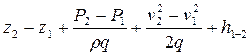 (5.14)
(5.14)
где 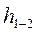 - потери напора в трубопроводе на участке 1-2. Разностью скоростных напоров в уравнении (5.14) на практике часто пренебрегают, так как скорости движения жидкости в трубопроводе малы и отличаются
- потери напора в трубопроводе на участке 1-2. Разностью скоростных напоров в уравнении (5.14) на практике часто пренебрегают, так как скорости движения жидкости в трубопроводе малы и отличаются
они на концах участка 1-2 незначительно (т.е. v1 = v2). В этом случае (5.14) примет более простой вид:
Нн = 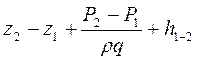 (5.15)
(5.15)
Отметим, что основными характеристиками гидравлического насоса, по которым осуществляют его выбор, являются напор Нн, м и подача
Q, м3/с.
5.1. Использование уравнения Бернулли в технике
5.1.1. Трубка Пито-Прандтля
Для измерения скорости потока при напорном движении жидкости на практике часто используются трубки Пито-Прандтля. Это средство измерения представляет собой систему из двух трубок, одна из которых прямая и направлена перпендикулярно потоку, а другая изогнута под углом 900 и направлена навстречу потоку (рис. 5.4).
Изогнутая трубка 2 измеряет полный гидродинамический напор h1, который исходя из уравнения Бернулли можно выразить уравнением (5.16):
h1 = z + p/ρg + v2/2g (5.16)
Прямая трубка 1, будет измерять пьезометрический напор h2 = z + p/ρg. Тогда перепад уровней жидкости в трубках h, представляющий собой разность h1 и h2 будет равен скоростному напору:
h = z + p/ρg + v2/2g – (z + p/ρg) = v2/2g (5.17)
Из выражения (5.17) местная скорость потока v может быть определена через перепад уровня h по уравнению (5.18):
v = 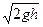 (5.18)
(5.18)
Для обеспечения более высокой правильности практических расчётов формула (5.18) используется с поправочным коэффициентом к, который является характеристикой трубки и определяется опытным путём, т.е.:
v = k 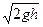 (5.19)
(5.19)
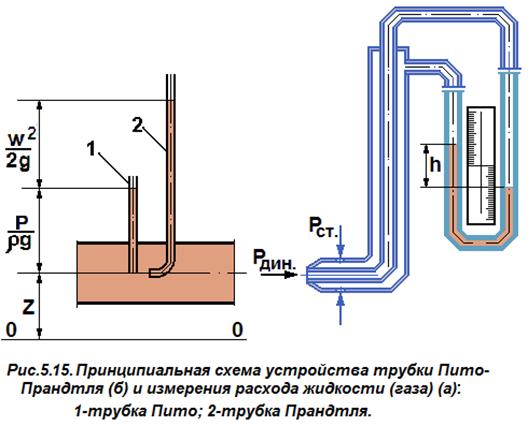

Рис. 5.4
На практике трубки Пито-Прандтля часто используются для определения объёмного расхода жидкости. В связи с наличием значительного градиента скорости по сечению потока, что особенно имеет место при движении реальных жидкостей, рекомендуется измерять скорости в нескольких точках сечения. Тогда объёмный расход будет определяться по формуле (5.19), где vср – средняя скорость потока, а S – площадь живого сечения.
Q = vсрS, м3/с (5.19)
