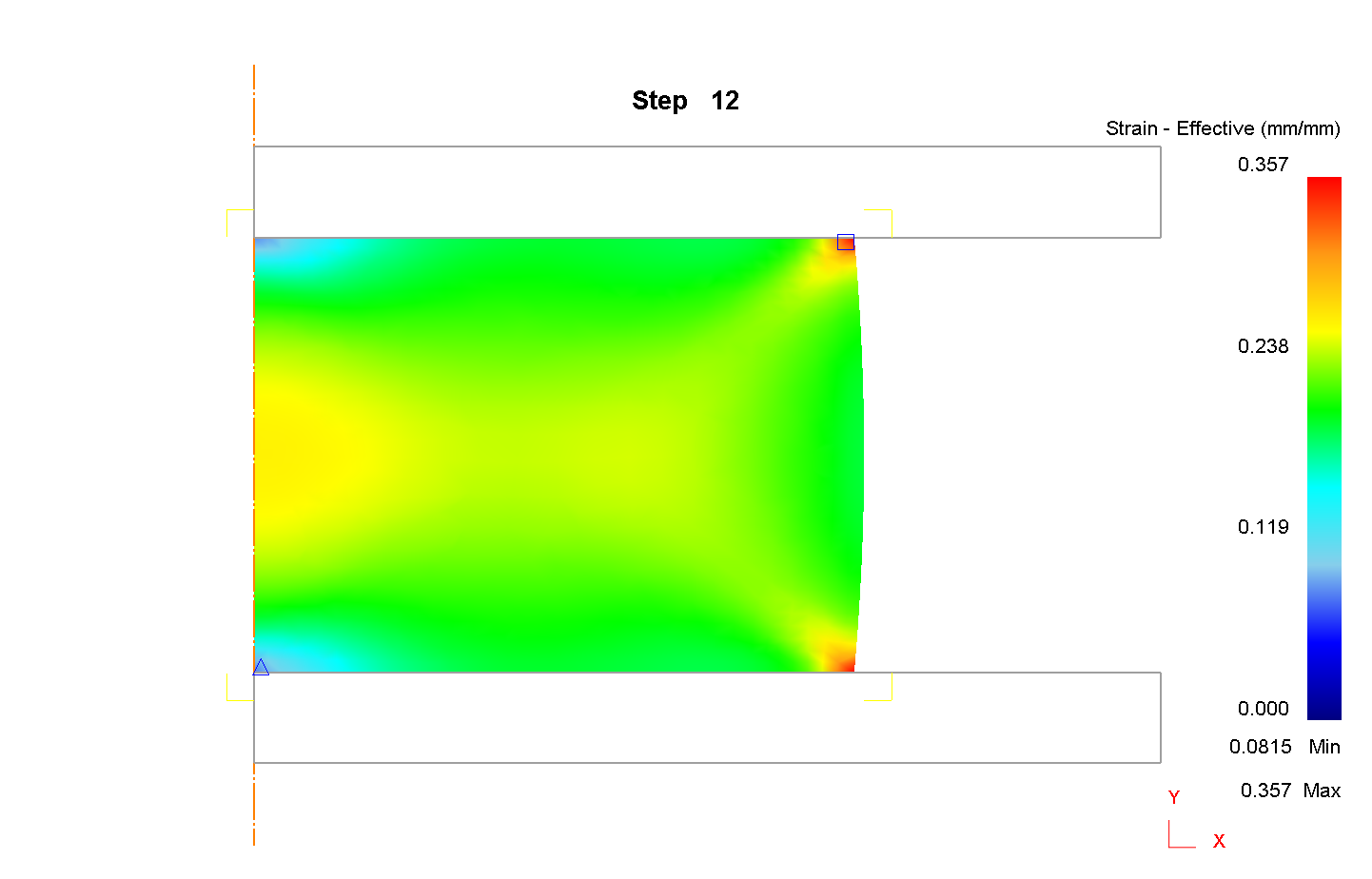
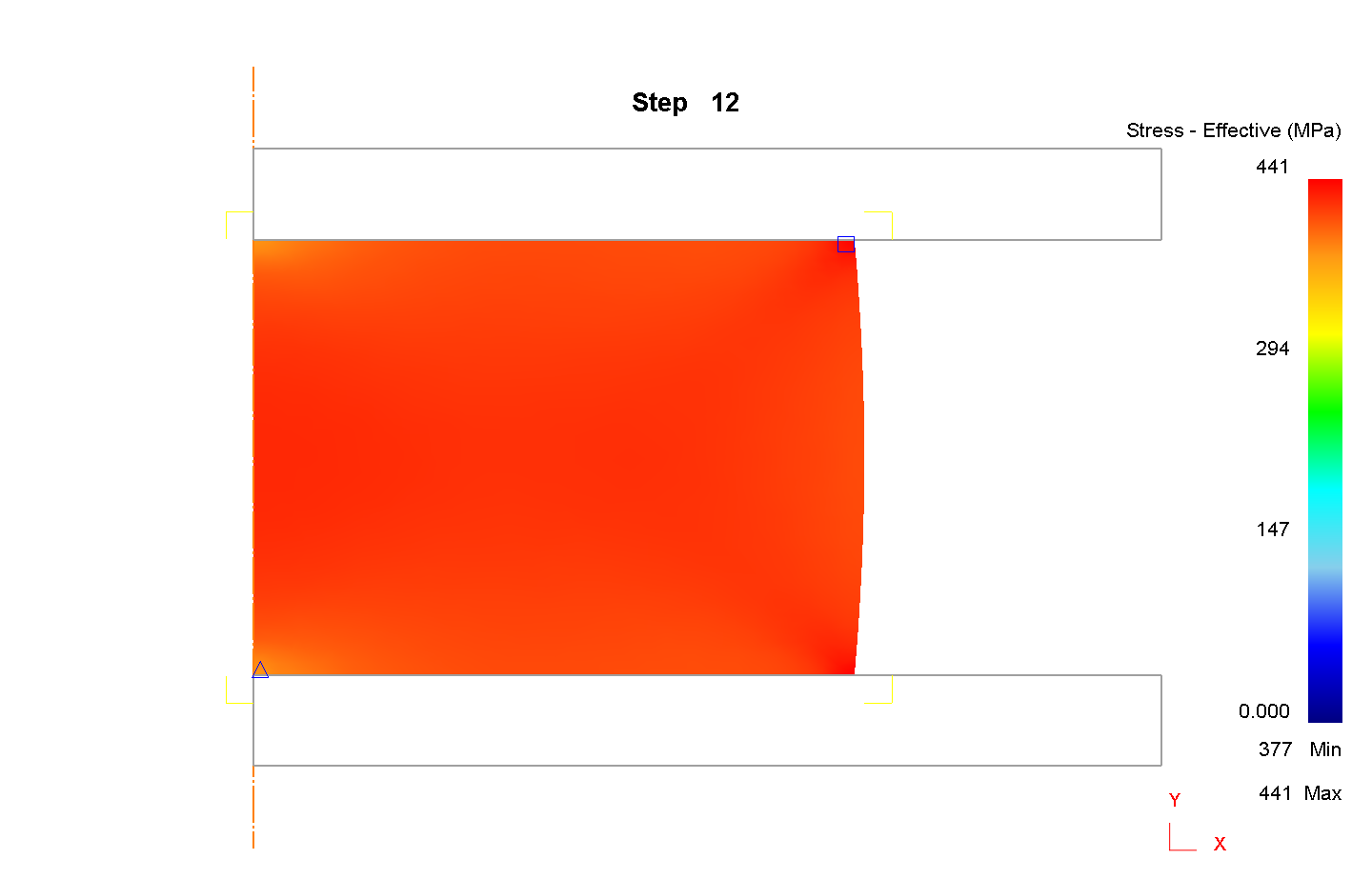
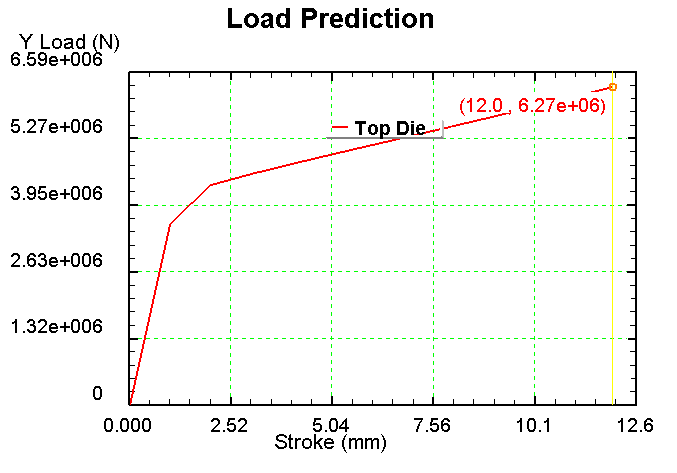
Обработка результатов эксперимента. Каждый эксперимент содержит элемент неопределенности вследствие ограниченности информации

Каждый эксперимент содержит элемент неопределенности вследствие ограниченности информации. Постановка параллель­ных опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта. Для ее определения опыт воспроизводится по возможности в оди­наковых условиях несколько раз и затем берется среднее арифметическое всех результатов

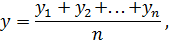
где n – число параллельных опытов.

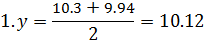
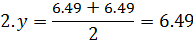
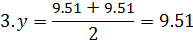
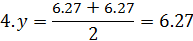
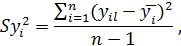
где 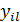– результат параметра оптимизации l – го повторения i – го опыта;

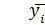– среднее арифметическое значение всех n повторений i – го опыта.

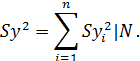
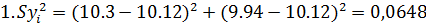
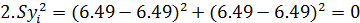
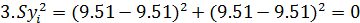
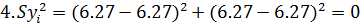
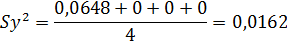
Таким образом, ставится серия одинаковых опытов n, затем про­веряется однородность дисперсий, т.е. выясняется, определяются ли различные значения у с одинаковой точностью по критерию Кохрена

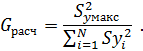
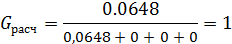
Расчетное значение G – критерия сравнивают с табличным в зависимости от уровня значимости 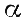, числа степеней свободы f = п — 1 и числа опытов N. Ряд дисперсий считается однородным, если G_расч < G_табл. 1< 0,9065, то есть ряд дисперсий неоднородный.

Проверка адекватности модели

Она необходима для того, чтобы ответить на вопрос — можно ли использовать полученное уравнение или необходима более сложная модель.

Адекватность модели проверяют с помощью критерии Фишера

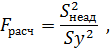
где 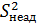– дисперсия неадекватности,

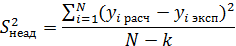
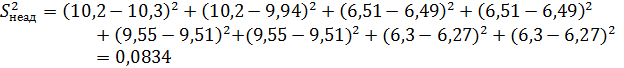
Здесь y_iрасч , y_iэксп — значения параметра оптимизации в i-м опыте, соответственно рассчитанные по уравнению регрессии и опреде­ленные экспериментально; k — число коэффициентов уравнения регрессии, включая b₀ .

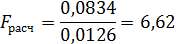
Гипотеза об адекватности уравнения принимается в том слу­чае, когда рассчитанное значение F-критерия не превышает табличного для выбранного уровня значимости и числа степеней сво­боды f₁, и f₂, с которым определялись дисперсии неадекватности опыта.

6,62 < 7,7, то есть наша модель адекватна.

Проверка статической значимости коэффициентов модели

Прежде всего, рассчитывается дисперсия в определении коэффициентов

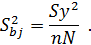
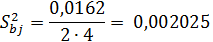
Коэффициент считается значимым, когда его абсолютная величина больше доверительного интервала, т. е.

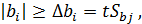
где t — критерий Стьюдента (берется из таблиц в зависимости oт уровня значимости а и числа степеней свободы при определении дисперсии опыта, табл. П2);

S_bj — среднеквадратичная ошибка определения коэффициентов

регрессии .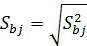

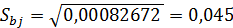
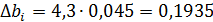
То есть значимые коэффициенты являются коэффициенты уравнения по максимальным окружным деформациям.

Приложение

I. Для ε=40%, μ=0,3

1) Сетка 1000 элементов

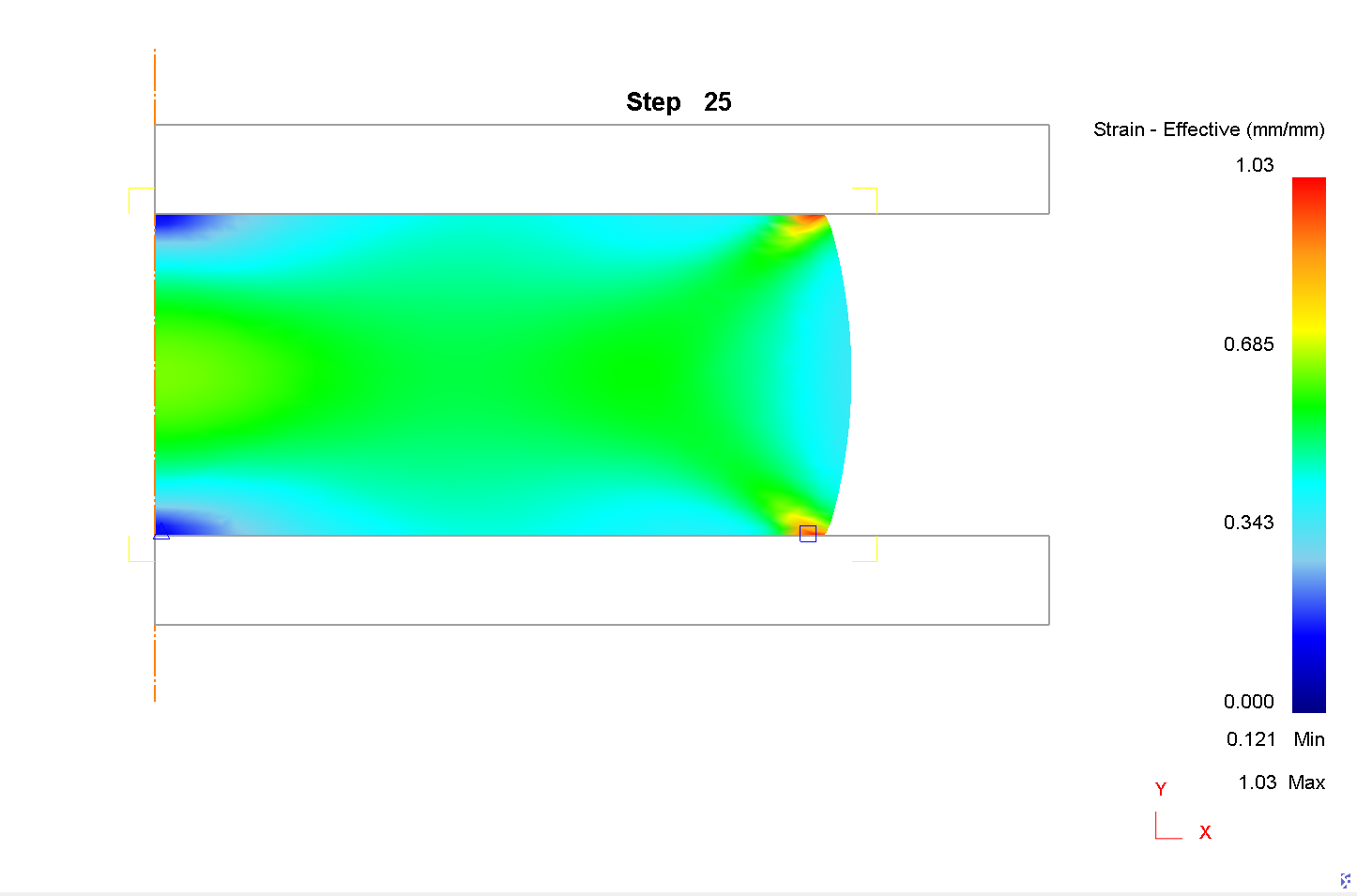
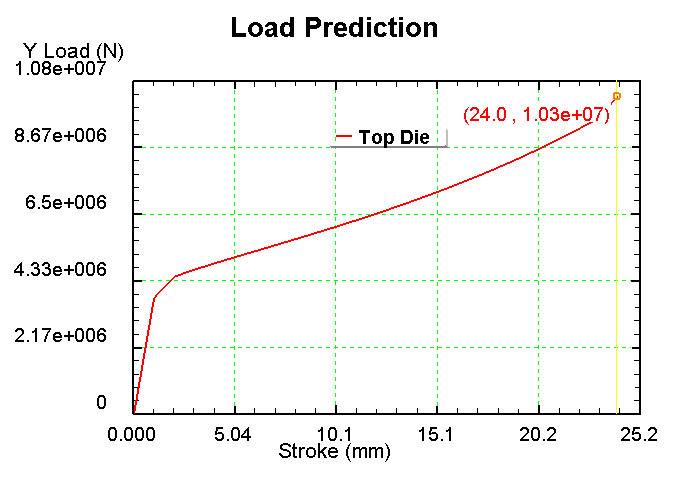
2) Сетка 900 элементов

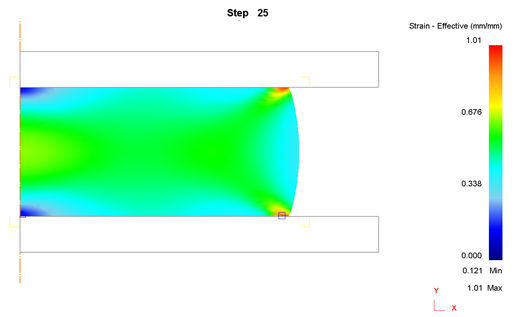
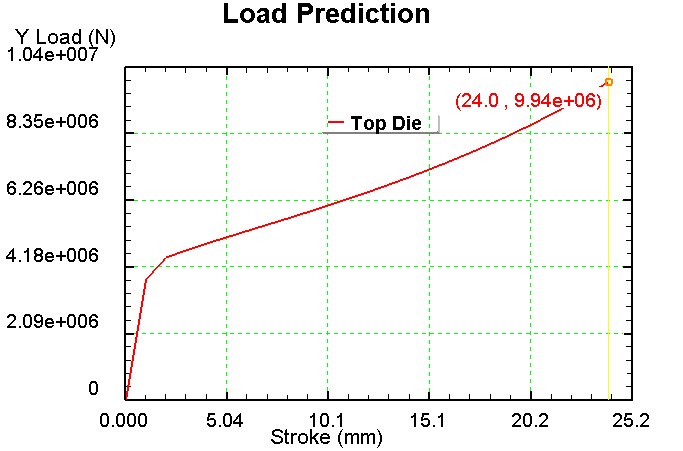
II. Для ε=20%, μ=0,3

1) Сетка 1000 элементов

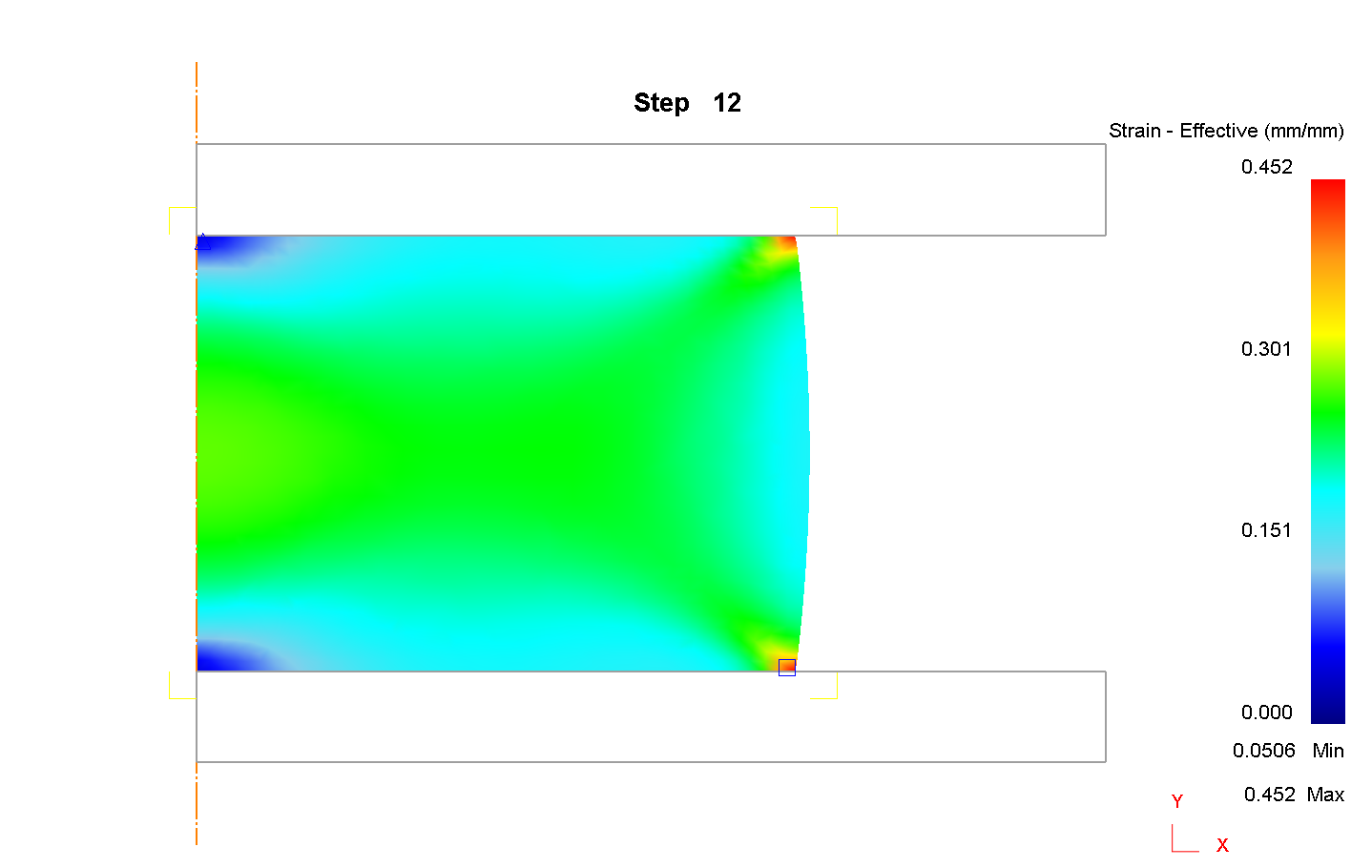
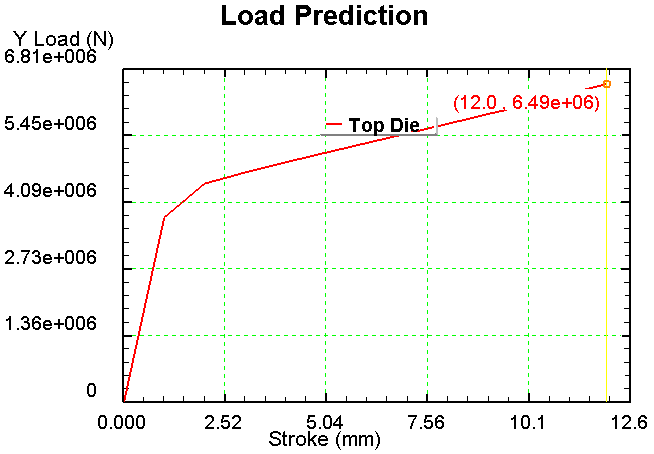
2) Сетка 900 элементов

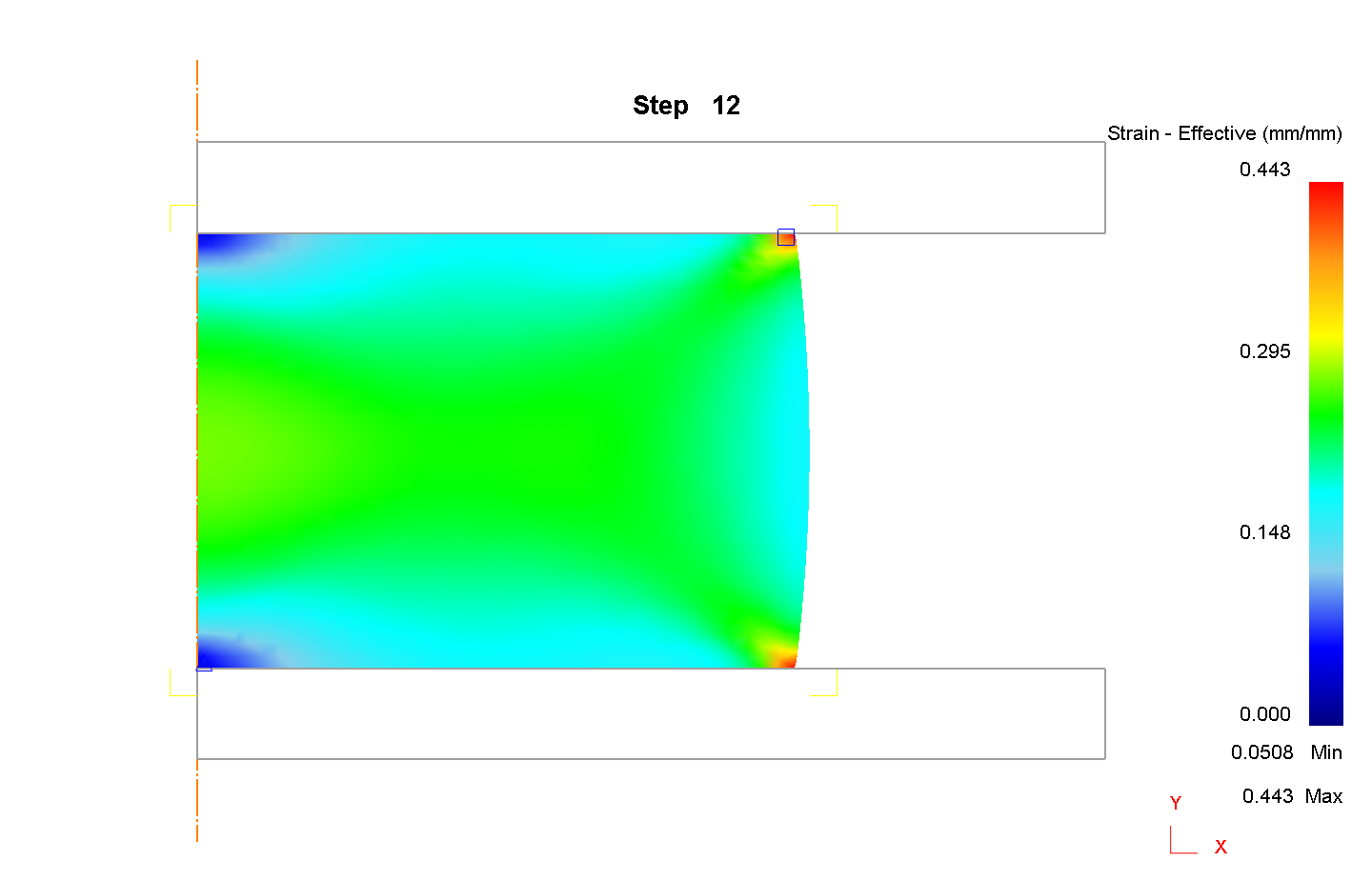
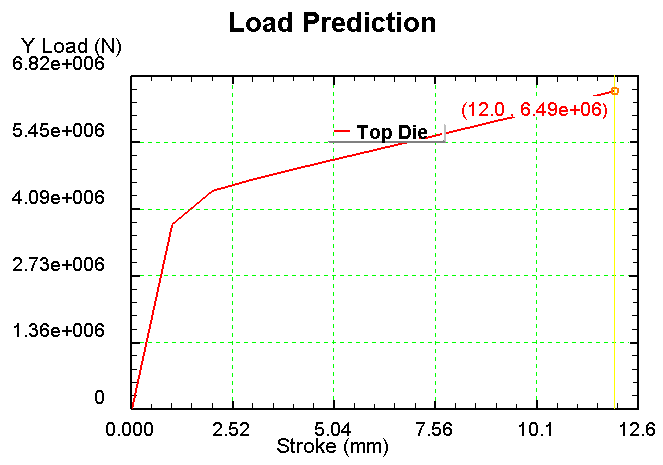
III. Для ε=40%, μ=0,2

1) Сетка 1000 элементов

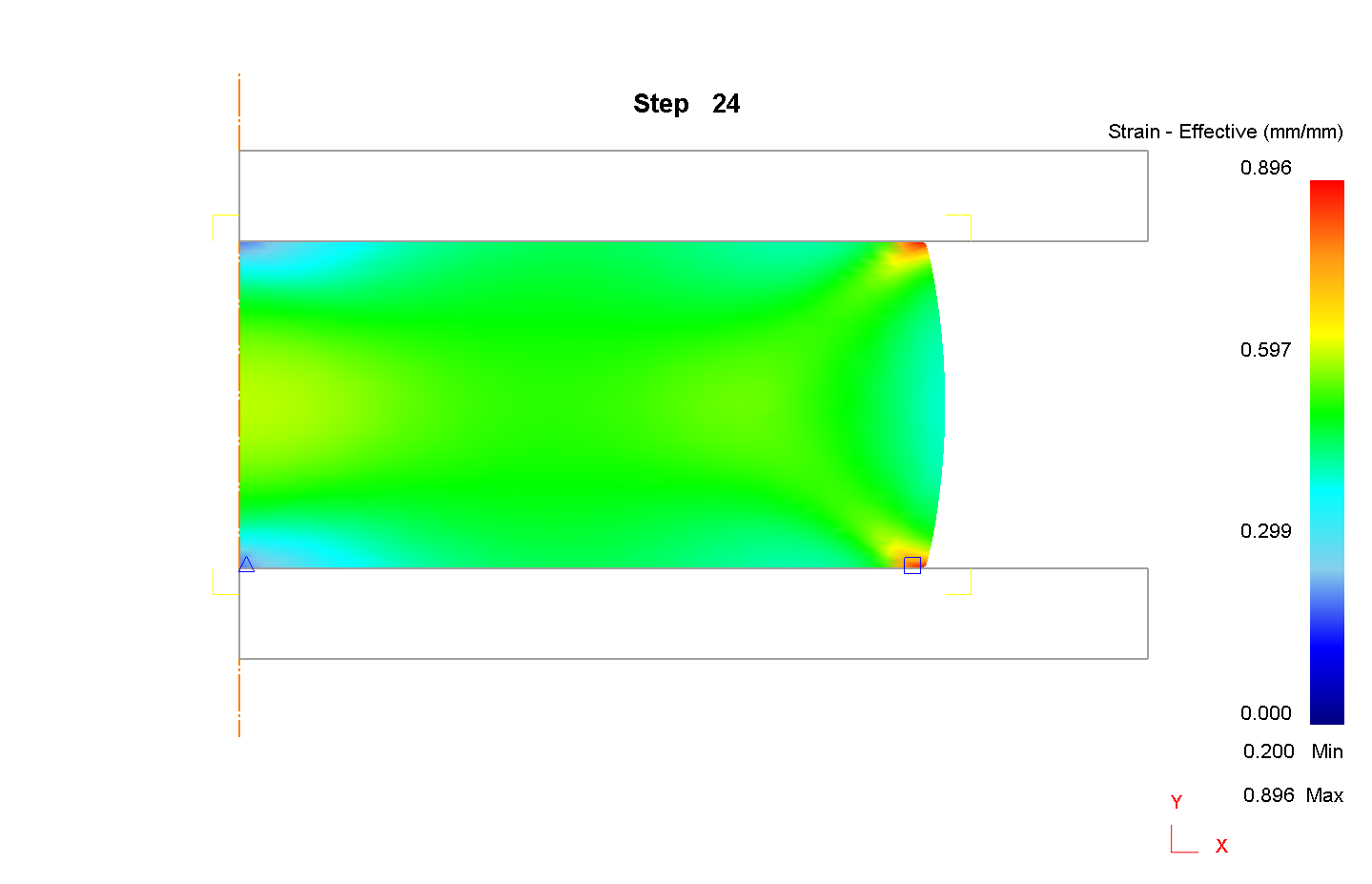
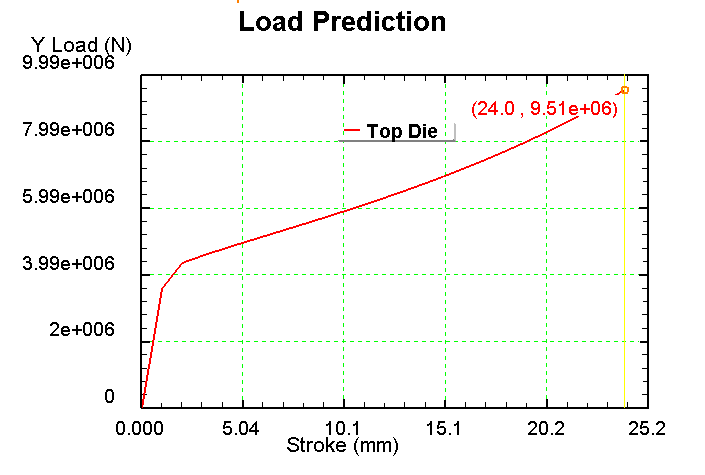
2) Сетка 900 элементов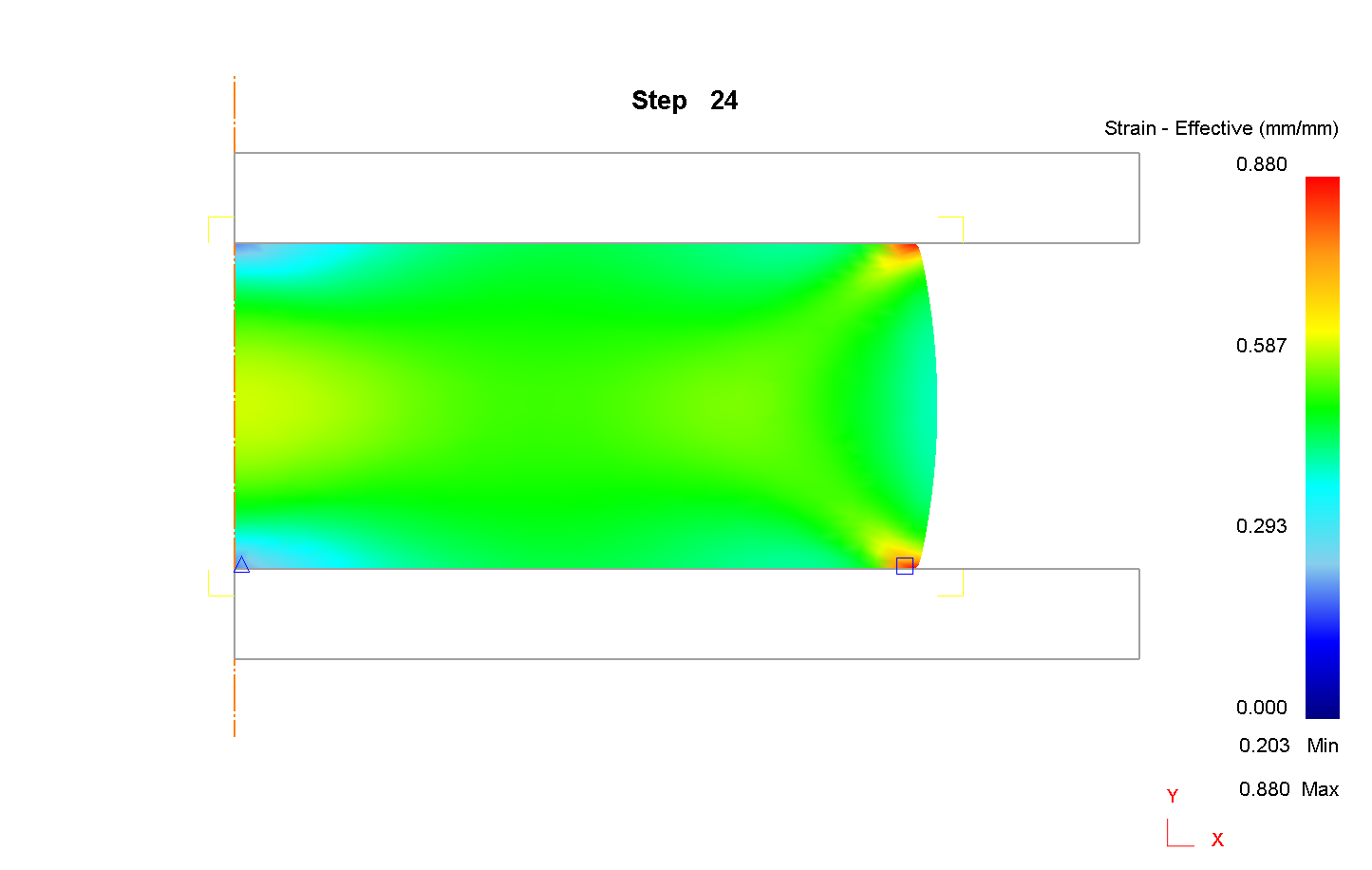

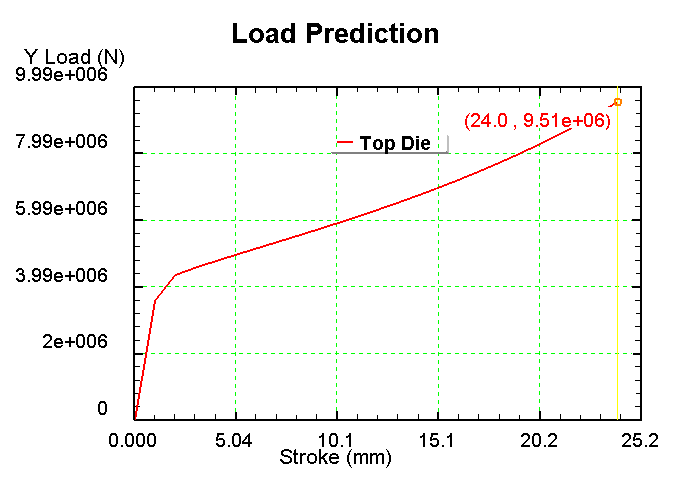
IV. Для ε=40%, μ=0,2

1) Сетка 1000 элементов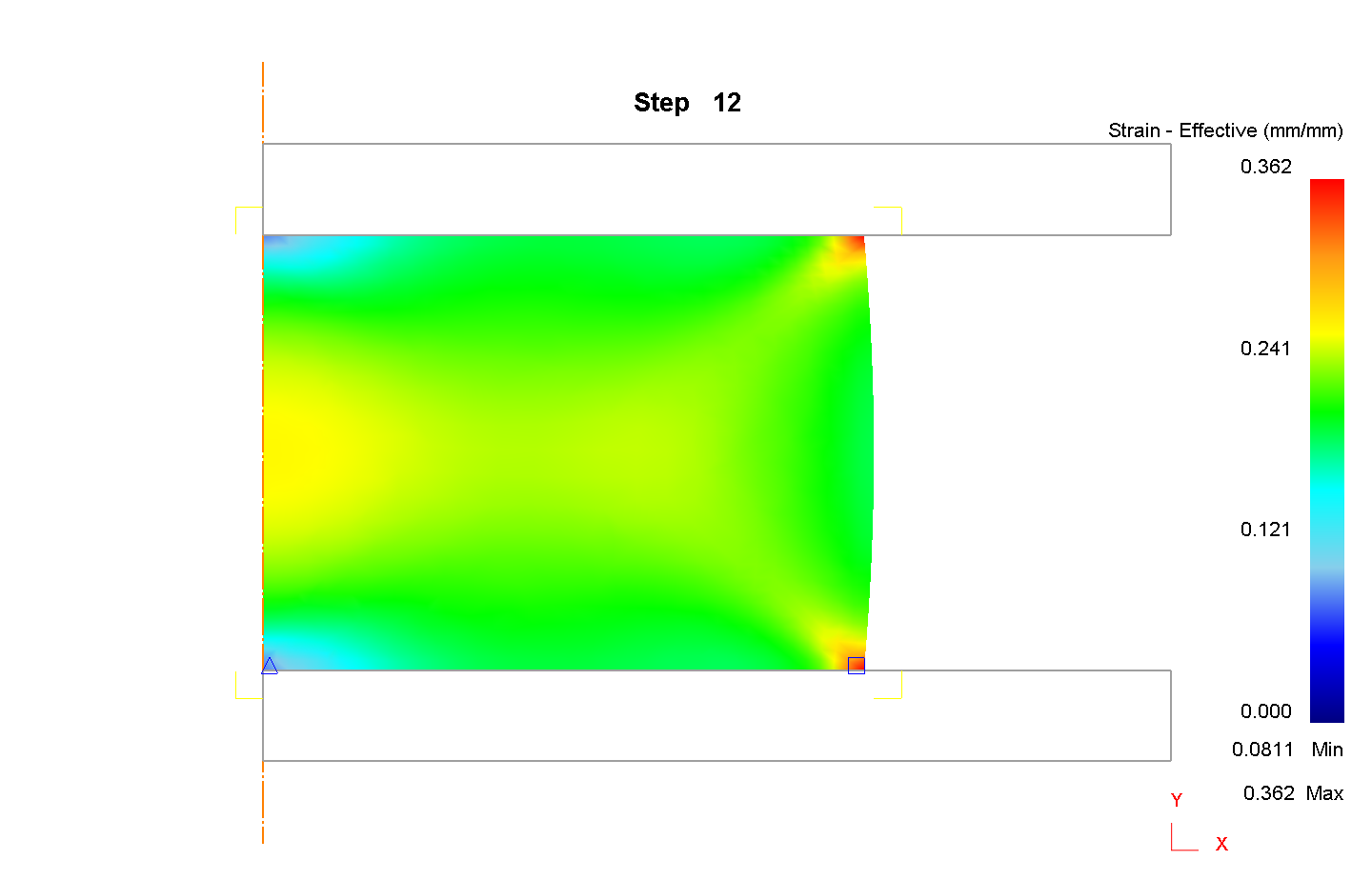

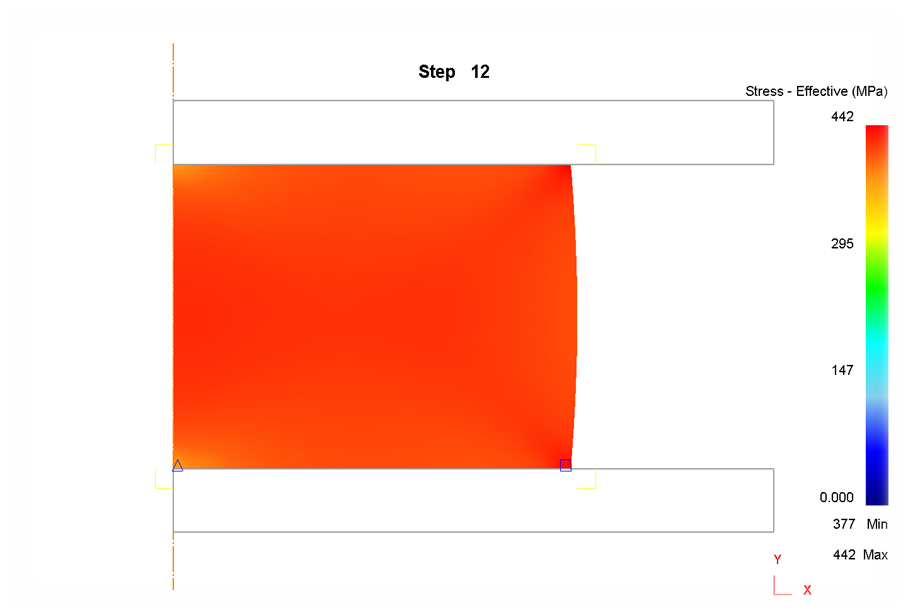
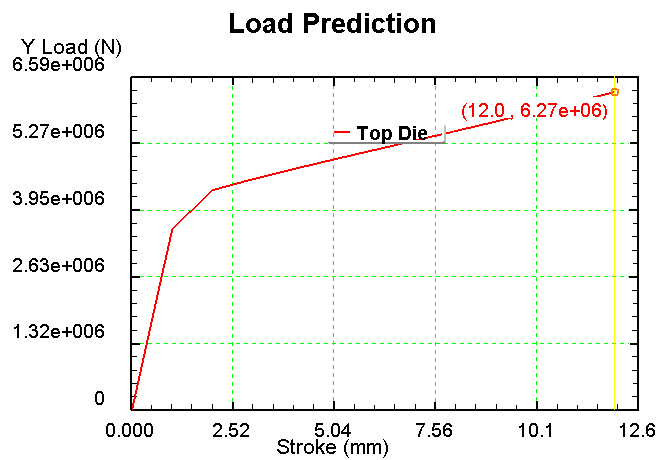
2) Сетка 900 элементов