Решение систем линейных уравнений методом Крамера.

Пусть нам требуется решить систему линейных алгебраических уравнений

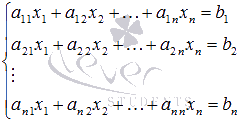
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .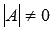

Пусть 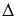- определитель основной матрицы системы, а 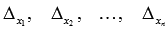- определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

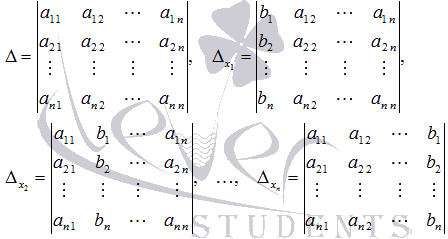
При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как 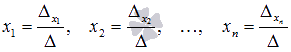. Так находится решение системы линейных алгебраических уравнений методом Крамера.

17. Матричный метод.

18. Метод Крамера.

19. Метод Гаусса.

20. Функция. Основные элементарные функции

21. Предел функции

22. Бесконечно малые и их основные свойства

23. Основные теоремы о пределах

Теорема 1. Предел постоянной величины равен самой постоянной:

c = c.

Теорема 2. Пределсуммы (разности) двух функций равен сумме (разности) их пределов:

= f(x)φ(x).

Теорема 3.Пределпроизведения двух функций равен произведению их пределов:

= f(x)φ(x).

Теорема 4. Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю:

, (картинка здесь должна быть)0.

Теорема 5. (О пределе промежуточной функции) Если в окрестности точки x0выполняются неравенства:

и = = А, то .

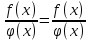
24. Первый замечательный предел

Первый замечательный предел
Первым замечательным пределом именуют следующее равенство:
limα→0sinαα=1(1)
Так как при α→0 имеем sinα→0, то говорят, что первый замечательный предел раскрывает неопределённость вида 00. Вообще говоря, в формуле (1) вместо переменной α под знаком синуса и в знаменателе может быть расположено любое выражение, – лишь бы выполнялись два условия:
Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида 00.
Выражения под знаком синуса и в знаменателе совпадают.
Часто используются также следствия из первого замечательного предела:
limα→0tgαα=1(2)
limα→0arcsinαα=1(3)
limα→0arctgαα=1(4)

25. Второй замечательный предел

26. Определение производной

27. Производная от сложной функции

28. Обратная функция и ее дифференцируемость

29. Обратные тригонометрические функции и ее дифференцируемость

Обра́тные тригонометри́ческие фу́нкции— математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

арксинус
арккосинус
арктангенс
арккотангенс
арксеканс
арккосеканс
🛑🛑🛑🛑🛑🛑🛑🛑🛑
Их дифференцируемость на фото vvv

30. Производные различных порядков

31. Дифференциал

32. Таблица основных формул дифференцирования

33. Производные: постоянной, произведения постоянной на функцию, суммы, произведения, частного