По подготовке к итоговой аттестации
Задача I.
Вычислить предел:
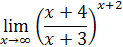
Решение:
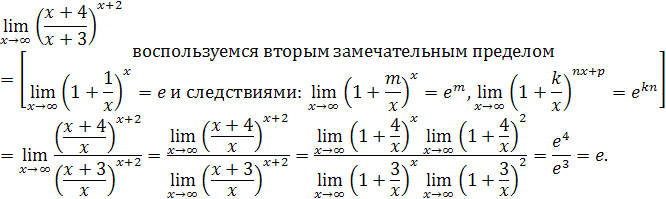
Задача II.
Вычислить неопределённые интегралы:
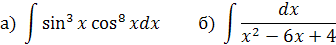
Решение:
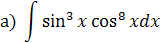
Полагая 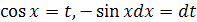 , получим:
, получим:
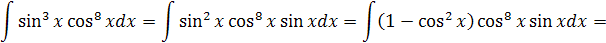
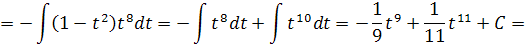
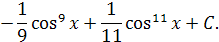
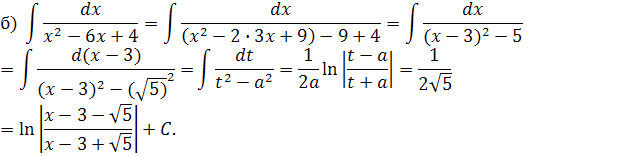
Задача III.
Вычислить определённые интегралы:
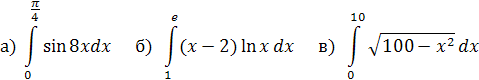
Решение:
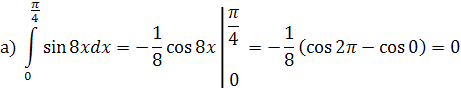
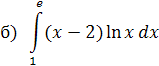
Интегрируем «по частям»:
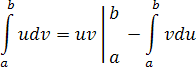
Пусть 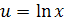 , тогда
, тогда 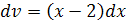 ,
,
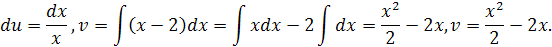
Имеем:
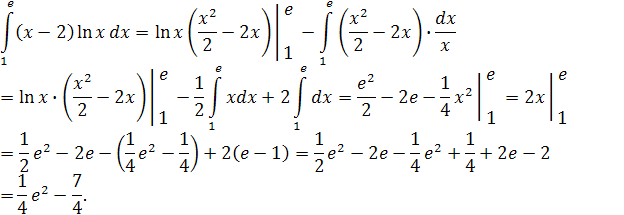
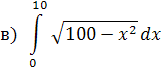
Интегрируем подстановкой.
Положим 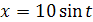 , тогда
, тогда 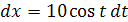 . Если
. Если  , то
, то 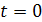 ; если
; если 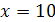 , то
, то 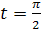 .
.
Поэтому
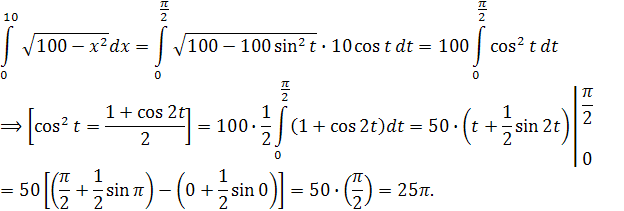
Заметим, что геометрически данный интеграл площадь круга:
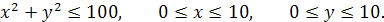
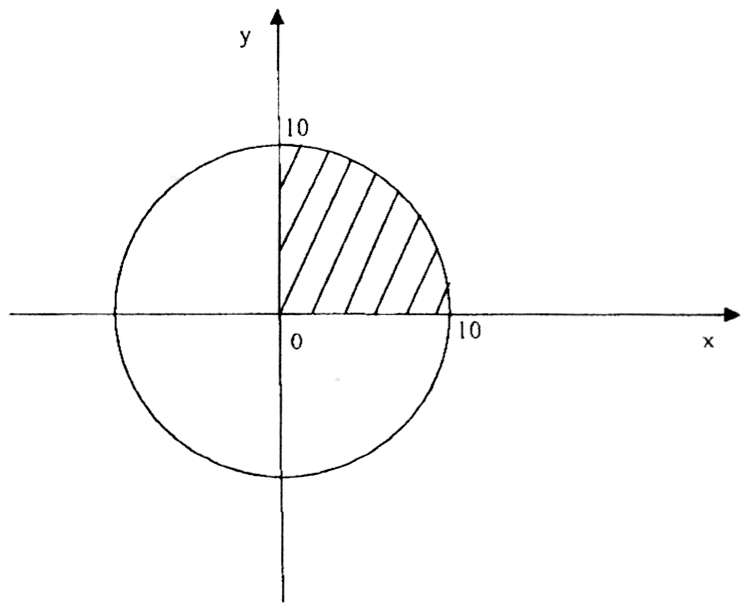
Задача IV.
Вычислить несобственные интегралы или установить их расходимость.
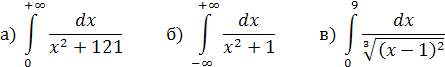
Решение:
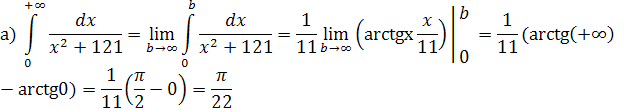
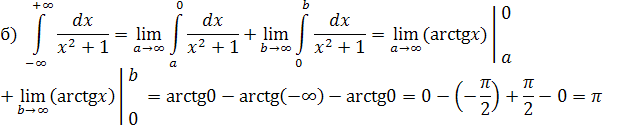
в) В данном случае подынтегральная функция 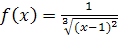 претерпевает разрыв в точке
претерпевает разрыв в точке 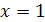 , лежащей внутри отрезка интегрирования
, лежащей внутри отрезка интегрирования 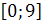 .
.
Имеем:
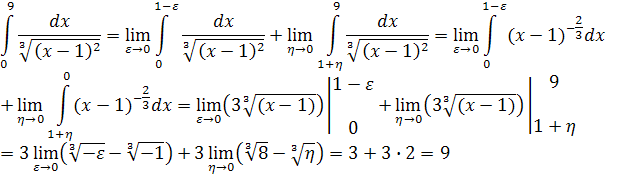
Задача V.
Вычислить объём тела, образованного вращением вокруг оси 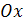 кривой:
кривой: 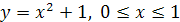 .
.
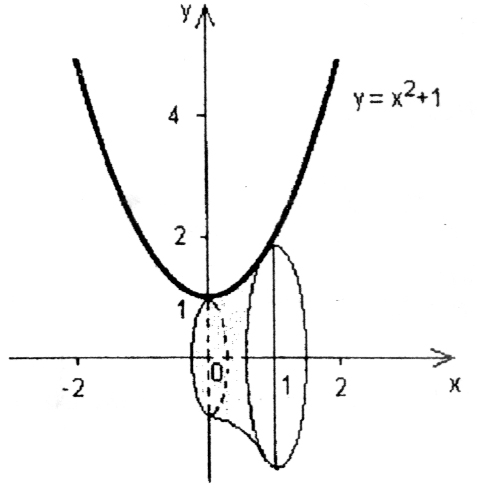
Объём фигуры, образованной вращение кривой 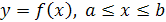 вокруг оси
вокруг оси 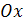 вычисляется по формуле:
вычисляется по формуле:
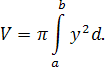
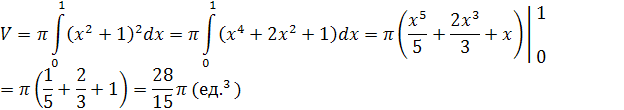
Задача VI.
Решить дифференциальные уравнения:
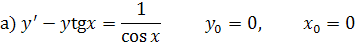
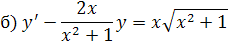
Решение:
Рассмотрим 2 метода решения.
1) Метод вариации произвольной постоянной (метод Лангранжа). Решим сначала уравнение 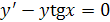 (линейное однородное уравнение).
(линейное однородное уравнение).
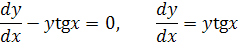
Разделяя переменные, получаем:
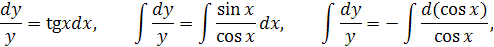
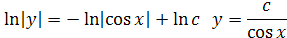
Найдём решение исходного (линейного неоднородного) уравнения в виде 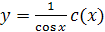 , где
, где 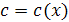 - неизвестная функция, которую надо найти.
- неизвестная функция, которую надо найти.
Имеем:
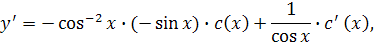
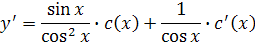
Подставим 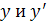 в исходное уравнение (линейное неоднородное).
в исходное уравнение (линейное неоднородное).
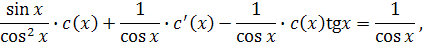
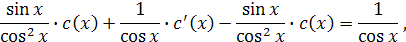
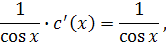
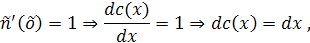
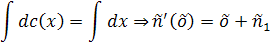
Найденную функцию 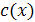 подставим в выражение
подставим в выражение 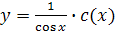 и получим
и получим 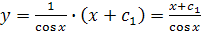 - общее решение исходного уравнения.
- общее решение исходного уравнения.
Найдём частное решение, удовлетворяющее начальным условиям 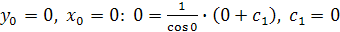 . Получим
. Получим 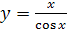 - искомое частное решение.
- искомое частное решение.
2) 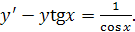
Метод подстановки (введение новых функций 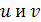 ). Пусть
). Пусть 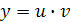 , где
, где 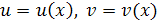 – неизвестные функции.
– неизвестные функции.
Имеем:
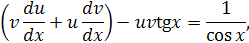
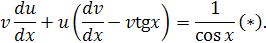
Поскольку одну из функций ( 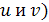 мы можем выбрать произвольно, положим
мы можем выбрать произвольно, положим
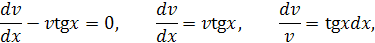
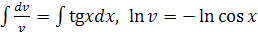 , при интегрировании мы опускаем модуль и
, при интегрировании мы опускаем модуль и 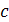 , т.к. нас интересует только одна функция, обращающая в нуль второе слагаемое
, т.к. нас интересует только одна функция, обращающая в нуль второе слагаемое  .
.
Итак,
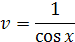
Подставим найденное выражение для 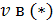 ; получаем:
; получаем:
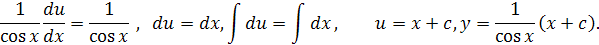
Получено то же общее решение, что и методом вариации произвольной постоянной.
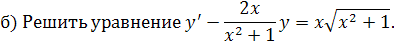
Это линейное уравнение первого порядка. Поэтому полагаем 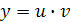 . Тогда
. Тогда 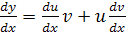 . Подставляя выражение для
. Подставляя выражение для 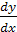 и
и  в данное уравнение, после группировки членов получим:
в данное уравнение, после группировки членов получим:
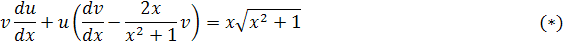
Выберем функцию 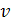 так, чтобы выполнялось равенство
так, чтобы выполнялось равенство
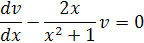
После распределения переменных это уравнение приме вид:
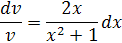
Почленное интегрирование дает 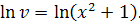
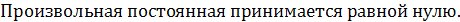
Подставив найденное выражение функции 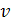 в равенство
в равенство  , получим
, получим 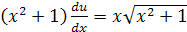 .
.
Это уравнение с разделяющимися переменными. Для нахождения функции 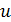 разделяем переменные и интегрируем:
разделяем переменные и интегрируем:
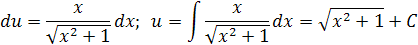
Теперь можно записать общее решение данного дифференциального уравнения:
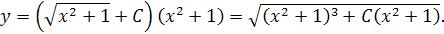
Задача VII.
Решить дифференциальные уравнения:
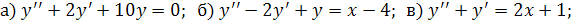
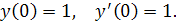
Решение:
а) Составим характеристическое уравнение. Для этого заменим 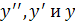 соответственно на
соответственно на 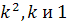 .
.
Характеристическое уравнение имеет вид:
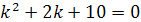
Данное уравнение имеет комплексные корни:
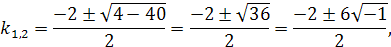
так как 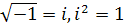 , то
, то 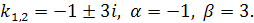
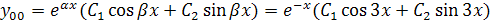 .
.
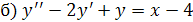 .
.
Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами, имеющие вид 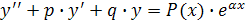 , где
, где 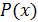 - какой-либо многочлен степени
- какой-либо многочлен степени 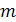 .
.
Общее решение данного уравнения есть сумма общего решения соответствующего линейного однородного уравнения 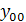 и частного решения данного неоднородного уравнения
и частного решения данного неоднородного уравнения 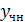 :
:
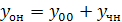
Частное решение 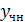 следует искать в виде
следует искать в виде 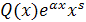 , где
, где 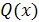 многочлен степени
многочлен степени 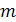 ; число
; число 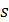 может принимать три значения:
может принимать три значения:
1. 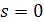 , если число
, если число 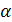 не является корнем характеристического уравнения
не является корнем характеристического уравнения 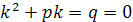 .
.
2. 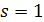 , если число
, если число 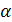 является однократным корнем характеристического уравнения:
является однократным корнем характеристического уравнения: 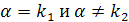 .
.
3. 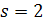 , если число
, если число 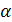 является двукратным корнем характеристического уравнения
является двукратным корнем характеристического уравнения 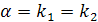 .
.
Составим характеристическое уравнение, заменив 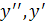 и
и  соответственно на
соответственно на 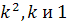 .
.
Характеристическое управление 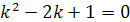 имеет корень
имеет корень 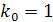 кратности 2.
кратности 2.
Общее решение линейного однородного уравнения найдём по формуле:
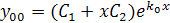
Подставив корень характеристического уравнения, получаем:
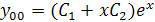
В исходном уравнении правая часть имеет вид:
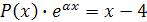 , т.е.
, т.е. 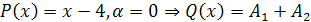
Так как 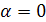 не является корнем характеристического уравнения, то частное решение данного линейного неоднородного уравнения ищется в виде
не является корнем характеристического уравнения, то частное решение данного линейного неоднородного уравнения ищется в виде 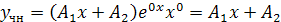 .
.
Для наводнения постоянных 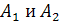 находим первую и вторую производные от
находим первую и вторую производные от 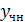 :
:
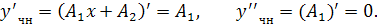
Подставляя в исходное уравнение 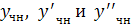 ,
,
имеем 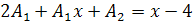 .
.
Приравнивая коэффициенты при одинаковых степенях 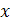 , получаем систему:
, получаем систему:
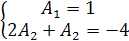 , из которой находим
, из которой находим 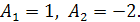
Следовательно, 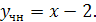
Общее решение уравнения 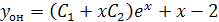 .
.
в) Найти общие и частное решения дифференциального уравнения.
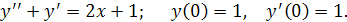
Найдём общее решение дифференциального уравнения.
Для этого составим характеристическое уравнение, заменив 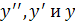 соответственно
соответственно 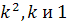 .
.
Характеристическое уравнение 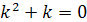 имеет корни
имеет корни 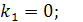
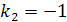 .
.
Общее решение линейного однородного уравнения найдем по формуле:
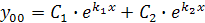
Подставив корни характеристического уравнения, получаем:
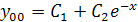
Так как 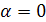 – однородный корень характеристического уравнения, то частное решение данного линейного неоднородного уравнения ищется в виде:
– однородный корень характеристического уравнения, то частное решение данного линейного неоднородного уравнения ищется в виде:

Подставляя в исходное уравнение 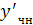 и
и 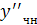 имеем:
имеем:
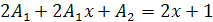
Приравнивая коэффициенты при одинаковых степенях 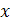 , получаем систему:
, получаем систему:
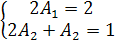 , из которой находим
, из которой находим 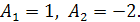
Следовательно, 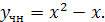
Общее решение уравнения 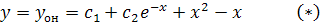
Найдём частное решение, удовлетворяющее условиям:
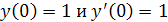 .
.
Дифференцируя 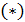 , получим
, получим 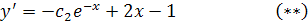
Подставляя начальные условия в 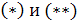 , получаем систему:
, получаем систему:
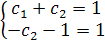
Отсюда 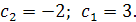
Искомое частное решение имеет вид 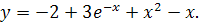
Задача VIII.
Определить область сходимости степенного ряда.
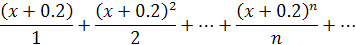
Решение:
Для ряда 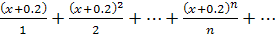 имеем
имеем
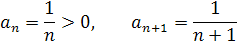
Найдём радиус сходимости ряда по формуле Д’Аламбера:
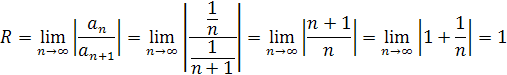
Следовательно, ряд обязательно абсолютно сходится, если:
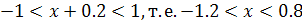
Исследуем сходимость ряда на концах промежутка 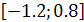 .
.
Если 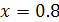 , то получаем ряд
, то получаем ряд 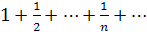 . Это гармонический ряд. Он расходится. Если
. Это гармонический ряд. Он расходится. Если 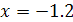 , то получаем ряд
, то получаем ряд 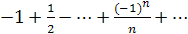 .
.
Имеем знакочередующийся ряд
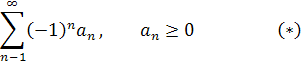
Применим признак Лейбница:
Ряд  сходится, если
сходится, если 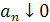 , т.е. модуль общего члена убывает и стремится к нулю при
, т.е. модуль общего члена убывает и стремится к нулю при 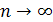 .
.
1. 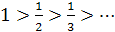 , т.е. модуль общего члена ряда убывает.
, т.е. модуль общего члена ряда убывает.
2. 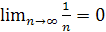 , т.е. модуль общего члена стремится к нулю при
, т.е. модуль общего члена стремится к нулю при 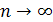 .
.
Ряд сходится условно.
Область сходимости есть промежуток 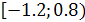 , сходимость на (
, сходимость на ( 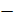 1.2; 0.8) абсолютная.
1.2; 0.8) абсолютная.
V. ЛИТЕРАТУРА
Основная
1. Шипачев, В. С. Основы высшей математики. / В. С Шипачев. М.: Высшая школа, 1998.
2. Письменный, Д. Т. Конспект лекций по высшей математике: в 2ч../ Письменный Д, Т. М.: Айрис-пресс, 2006. Ч.1,2.
3. Баврин, И.И. Высшая математика / Баврин И.И. М: Академия, Высшая школа, 2000.
4. Чвялева, М.Д. Методическое пособие по математике/Н.И.Чвялева. Екатеринбург: УрГЭУ, 2008.
Дополнительная
1. Данко, П.Е. Высшая математика в упражнениях и задачах: в 2 ч. / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. М.:ОНИКС XXI век: Мир и Образование, 2003. Ч. I.
2. Шипачев, B.C. Сборник задач по высшей математике. / В.С.Шипачев М.: Высшая школа,2006.
3. Лунгу, К. Н. Сборник задач по высшей математике. 1 курс. / Лунгу К. Н., Письменный Д. Т., Федин С. Н. и др. М.: Айрис-пресс, 2005.
4. Лунгу, К. Н. Сборник задач по высшей математике. 2 курс. / Лунгу К. Н., Письменный Д. Т., Федин С. Н. и др. М.: Айрис-пресс, 2006.
5. Практикум по высшей математике для экономистов / под ред. Н.Ш. Кремера. М.: ЮНИТИ-ДАНА, 2004.
