Применение программы МС9 для научных исследований
Часто в процессе научной работы встречаются ситуации, когда теоретический анализ работы какого-либо устройства слишком сложен, а реализация устройства «в железе» по каким-то причинам невозможна. Такие ситуации, как правило, возникают, когда анализируемое устройство появляется не в результате математического синтеза, а в процессе эмпирического изобретательства. В таких условиях неоценимую помощь может оказать моделирование и, в частности, программа МС9.
В качестве иллюстрации сказанного приведем несколько примеров.
Пример.
До сих пор, говоря о работе адаптивного компенсатора помех, мы молчаливо предполагали, что помеховые сигналы в основном и дополнительном каналах имеют одинаковую начальную фазу. В практических задачах это условие выполняется крайне редко. Тем не менее, идея компенсации, заложенная в основе алгоритма Уидроу, слишком привлекательна, чтобы от нее можно было легко отказаться. Именно поэтому была предложена, так называемая, «квадратурная» схема адаптивного компенсатора помех (рисунок 5.47).
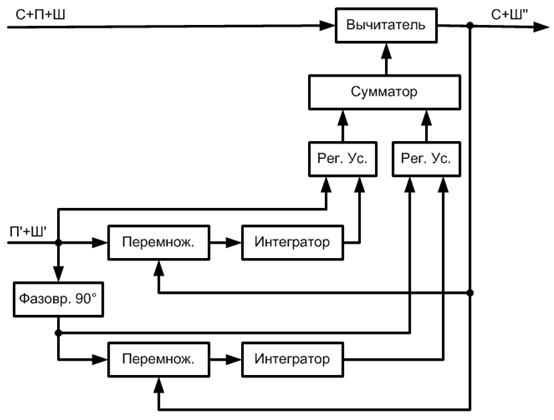
Рисунок 5.47 – Структурная схема квадратурного компенсатора помех
От классической эта схема отличается тем, что в дополнительном канале с помощью фазовращателя на 90˚ организуются синфазный и квадратурный каналы обработки со своими отдельными корреляторами и регулируемыми усилителями. Корреляторы в каждом канале формируют напряжения, пропорциональные коэффициентам корреляции между неподавленным остатком помехи на выходе компенсатора и сигналами синфазного и квадратурного каналов. Эти напряжения управляют коэффициентами передачи регулируемых усилителей. В процессе работы, на выходе сумматора напряжение помехи изменяет не только амплитуду, но и фазу, стремясь к амплитуде и фазе помехи в основном канале. Благодаря этому, на выходе устройства происходит компенсация помехи.
Проверить работоспособность устройства и определить его параметры можно с помощью модели, показанной на рисунке 5.48.
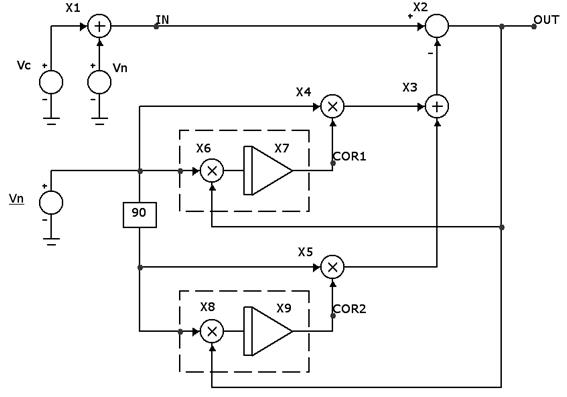
Рисунок 5.48 – Квадратурный компенсатор помех
Особенностью схемы является введение макромодели фазовращателя на 90˚ для получения квадратурной составляющей помехи. Корреляторы в каждом канале, состоящие из перемножителя и интегратора, обведены пунктирной линией. Кроме того, генератор помехи Vn формирует помеховый сигнал со сдвигом начальной фазы на 30˚ относительно помехи в основном канале. Для получения наглядных результатов, при моделировании считалось, что компенсатор работает в условиях отсутствия флуктуационных шумов в основном и дополнительном каналах, а также параметры генераторов сигнала и помехи выбраны такими же, как в примере п. 5.2.17.
Результаты моделирования показаны на рисунке 5.49. На графики выведены выходное напряжение компенсатора и уровень напряжения корреляторов, управляющих коэффициентами передачи регулируемых усилителей.
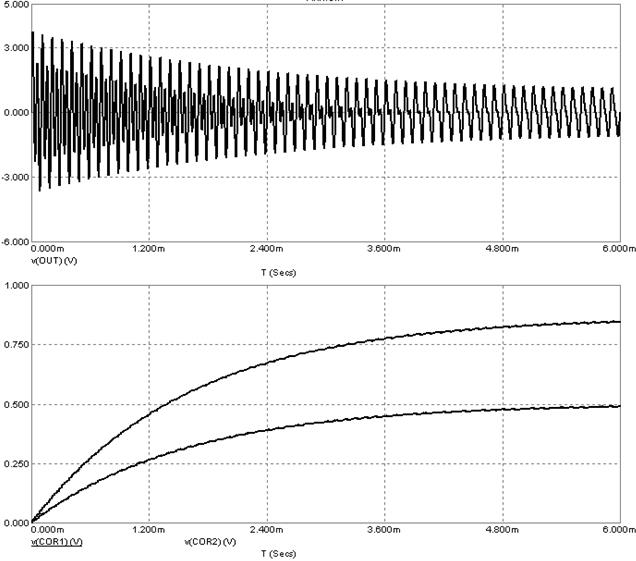
Рисунок 5.49 –Временные диаграммы выходного сигнала и коэффициентов передачи регулируемых усилителей квадратурного компенсатора
Видно, что в процессе работы уровень помехи на выходе компенсатора снижается. Кроме всего прочего, это хорошо видно и в том, что выходной сигнал становится все более «синусоидальным», соответствующем полезному сигналу. Если уровень или фаза помехового сигнала в основном или дополнительном каналах будет изменяться, контуры адаптации будут автоматически подстраивать коэффициенты передачи регулируемых усилителей для минимизации помехи на выходе.
Пример.
Ранее была приведена структурная схема адаптивного компенсатора помех и результаты моделирования его работы в простейших условиях.
При практической реализации этой схемы могут возникнуть проблемы, связанные с необходимостью увеличения коэффициента усиления, что в ряде случаев невозможно из-за ограниченного динамического диапазона цепи настройки (в частности, регулируемого усилителя). Кроме этого, при больших уровнях помехи в основном и дополнительном каналах невозможно обеспечить компенсирующий сигнал необходимого уровня из-за нелинейности передаточной характеристики регулируемого усилителя.
Для повышения эффективности адаптивного компенсатора помех предложена схема, приведенная на рисунке 5.50. Данное техническое решение позволяет значительно уменьшить время адаптации (либо при том же времени адаптации уменьшить остаточную ошибку компенсации) и одновременно расширить динамический диапазон канала настройки путем введения дополнительного весового коэффициента в основной канал приема.
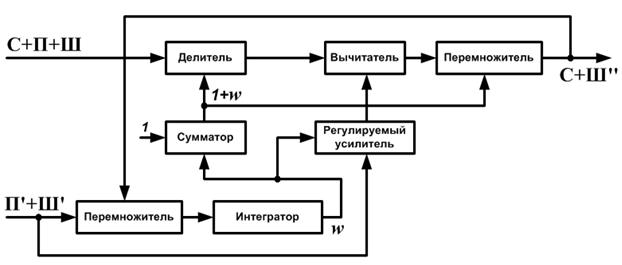
Рисунок 5.50. Структурная схема модифицированного
адаптивного компенсатора помех
Схема работает следующим образом. При наличии помехи на входе основного и дополнительного каналов возрастает весовой коэффициент w на выходе коррелятора, увеличивая коэффициент передачи регулируемого усилителя и, следовательно, долю помехи на втором входе вычитателя. Одновременно с этим снижается уровень сигнала в основном канале (на первом входе вычитателя). Это производится с помощью делителя, на втором входе которого формируется весовой коэффициент (1 + w). Таким образом, настройка ведется одновременно по основному и дополнительному каналу, ускоряя процесс адаптации. Тем самым уменьшается время сходимости без изменения постоянной времени интегратора. Для восстановления уровня сигнала основного канала до исходной величины на выходе вычитателя может применен дополнительный перемножитель.
На рисунках …5.51 – 5.54 приведены результаты сравнительного моделирования традиционного (рисунок 5.45) и модифицированного адаптивных компенсаторов помех. Для наглядности исследование динамических свойств производилось в отсутствии полезного сигнала и шума, при одинаковых уровнях помехи на входе основного и дополнительного каналов.
Видно, что время установления (время достижения уровня 0.9 от установившегося значения) для модифицированной схемы уменьшается примерно в 2 раза по сравнению с известной схемой.
Сравнительный анализ можно произвести с помощью различных зависимостей. На рисунке 5.51 приведены кривые настройки весовых коэффициентов для обеих схем компенсаторов, причем зависимости были пронормированы относительно установившегося значения. На рисунке 5.52 показаны осциллограммы сигнала ошибки, наглядно демонстрирующие преимущества модифицированного алгоритма. На рисунках 5.53, 5.54 сравнение производится на фазовой плоскости по виду фазовой траектории сигнала ошибки. Из рисунков видно, что при одинаковых начальных условиях фазовая траектория для модифицированной схемы значительно быстрее достигает установившегося значения.
|
|
|


|
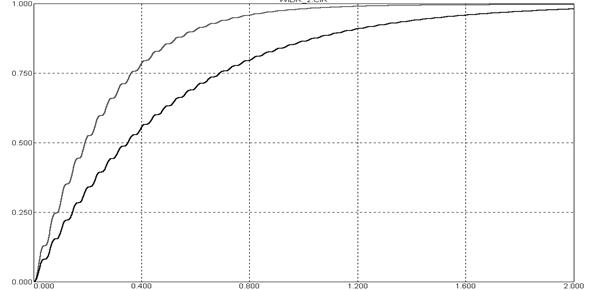
Рисунок 5.51 – Нормированные кривые настройки весовых коэффициентов компенсатора:
а – для традиционной схемы;
б – для модифицированной схемы.
|
|

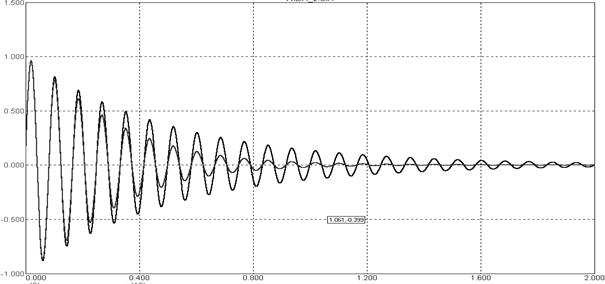
Рисунок 5.52 – Временные характеристики сигнала ошибки на выходе компенсатора:
а – для традиционной схемы;
б – для модифицированной схемы.
|
|
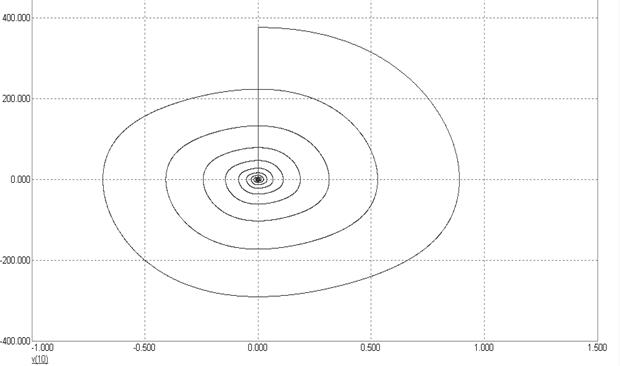
Рисунок 5.53 – Фазовая траектория традиционной схемы адаптивного компенсатора помех
|
|
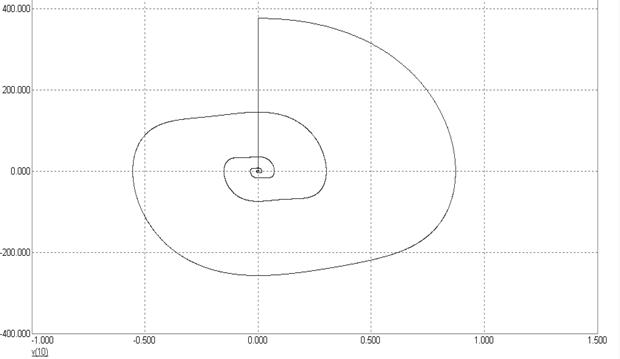
Рисунок 5.54 – Фазовая траектория модифицированной схемы компенсатора
с дополнительным весовым коэффициентом в основном канале
Приведенные примеры дают далеко не исчерпывающую картину применения программы МС9 для исследования сложных устройств или систем, теоретический анализ которых чрезвычайно труден из-за используемого математического аппарата. Показанный подход может быть чрезвычайно полезным и при проектировании различных устройств.
ЗАКЛЮЧЕНИЕ
Согласно сведениям, размещенным на сайтах фирм – разработчиков программного обеспечения для проектирования и моделирования радиоэлектронных устройств, число зарегистрированных пользователей данного программного продукта в 2008 году перевалило за 250 тыс. Причем основными пользователями программ являются учащиеся высших и средних учебных заведений.
В процессе знакомства с приведенными в настоящем учебном пособии программами схемотехнического моделирования и примерами их применений можно легко убедиться, что они являются удобным инструментом учебного процесса лабораторного практикума по таким предметам, как основы теории цепей, электронных приборов, вычислительной техники и автоматики и т.д. Практика показала, что минимальная предварительная подготовка позволяет студентам приступать к самостоятельной работе.
Описанные в пособии программы также могут оказаться полезными при выполнении различных расчетно-графических заданий, курсовых и дипломных проектов. Особенно важно подчеркнуть, что при этом можно использовать мощные средства визуализации и документирования, которыми обладают рассмотренные программы.
Наконец, можно отметить, что возможности программ при моделировании функциональных схем, делают возможным использовать их при проведении научных исследований в самых разнообразных направлениях радиотехнических устройств и устройств телекоммуникаций.
ЛИТЕРАТУРА
1. Левин Б.Р., Шварц В. Вероятностные модели и методы в системах связи и управления. – М.: Радио и связь, 1985. – 312 с. – (Статистическая теория связи. Вып. 24).
2. Разевиг В.Д. Применение программы P-CAD и PSpice для схемотехнического моделирования на ПЭВМ В 4 выпусках. М.: Радио и связь, 1992.
3. Разевиг В.Д. Система схемотехнического моделирования и проектирования печатных плат Design Center PSpice.– М.: СК Пресс, 1996. –272 с., ил.
4. Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и ее применение. –М.: Солон-Р, 1999.
5. Разевиг В.Д. Схемотехническое моделирование с помощью Micro-Cap 7. – М.: Горячая линия–Телеком, 2003. – 268 с.:ил.
6. Разевиг В.Д. Универсальная программа проектирования электронных устройств ALPAC // PC Week/RE, 1997, № 26.– с. 45-46.
7. Уидроу Б., Стирнз С. Адаптивная обработка сигналов. – М.: «Радио и связь», 1989. – 440с.
8. Травин Г.А. Основы схемотехники. Часть 1: Учебник.– М.: «Высшая школа»., 2005. – 201с.
9. Травин Г.А. Основы схемотехники. Часть 2: Учебник / СибГУТИ. – Новосибирск, 2006. – 381с.
10. Архипов С.Н. Моделирование аналоговых устройств с применением программы Electronics Workbench. – Метод. указания / СибГУТИ - Новосибирск, 2004. – 40с.
11. Архипов С.Н., Михеенко А.М. Компьютерное моделирование электронных схем в среде PSpice . – Метод. указания / СибГУТИ - Новосибирск, 2000. – 40с.
12. Чухров А.С., Архипов С.Н. Моделирование импульсных и логических устройств с применением программы Electronics Workbench. – Метод. указания / СибГУТИ - Новосибирск, 2004. – 29с.
АрхиповСергей Николаевич
ЧухровАлександр Семенович
Основы компьютерного моделирования устройств телекоммуникаций
Учебное пособие
Редактор: М.Г. Кокорич
Корректор: Д.С. Шкитина
Верстка и техническое редактирование: А.В. Колмогорова
Подписано в печать
Формат бумаги 60 х 84/16, отпечатано на ризографе, шрифт №10,
изд. л. заказ № тираж 150, СибГУТИ
630102, Новосибирск, ул. Кирова, 86