Решение невырожденных линейных систем.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К выполнению контрольной работы

Контрольная работа должна быть сделана в отдельной тетради, на обложке которой студенту следует разборчиво написать свою фамилию, инициалы, шифр, название дисциплины.

Решения задач необходимо проводить в той же последовательности, что и в условиях задач. При этом условие задачи должно быть полностью переписано перед ее решением.

Студент выполняет тот вариант контрольной работы, который совпадает с двумя последними цифрами его учебного шифра.

		Последняя цифра номера зачетной книжки
Предпоследняя цифра номера зачетной книжки		1, 31, 61, 91, 121, 151	2, 32, 62, 92, 122, 152	3, 33, 63, 93, 123, 153	4, 34, 64, 94, 124, 154	5, 35, 65, 95, 125, 155
	11, 41, 71, 101, 131, 161	12, 42, 72, 102, 132, 162	13, 43, 73, 103, 133, 163	14, 44, 74, 104, 134, 164	15, 45, 75, 105, 135, 165
	21, 51, 81, 111, 141, 171	22, 52, 82, 112, 142, 172	23, 53, 83, 113, 143, 173	24, 54, 84, 114, 144, 174	25, 55, 85, 115, 145, 175
	20, 41, 80, 101, 131, 161	19, 40, 79, 100, 130, 162	18, 39, 78, 99, 129, 163	17, 38, 77, 98, 128, 164	16, 37, 76, 97, 127, 165
	10, 31, 70, 91, 121, 171	9, 51, 69, 111, 141, 172	8, 52, 68, 112, 142, 173	7, 53, 67, 113, 143, 174	6, 54, 66, 114, 144, 175
	30, 60, 90, 120, 150, 151	29, 40, 89, 100, 130, 152	28, 41, 88, 101, 131, 153	27, 42, 87, 102, 132, 154	26, 43, 86, 103, 133, 155
	2, 49, 62, 109, 139, 161	3, 50, 63, 110, 140, 162	4, 51, 64, 111, 141, 163	5, 52, 65, 112, 142, 164	6, 53, 64, 113, 143, 165
	12, 59, 72, 119, 149, 171	13, 60, 73, 120, 150, 172	14, 31, 74, 91, 121, 173	15, 32, 75, 92, 122, 174	16, 33, 76, 93, 123, 175
	22, 39, 82, 99, 129, 161	23, 40, 83, 100, 130, 159	24, 42, 84, 101, 131, 158	25, 42, 85, 102, 132, 157	26, 43, 86, 103, 133, 156
	15, 49, 75, 109, 139, 171	14, 50, 74, 110, 140, 172	13, 51, 73, 111, 141, 173	12, 52, 72, 112, 142, 174	11, 53, 71, 113, 143, 175

		Последняя цифра номера зачетной книжки
Предпоследняя цифра номера зачетной книжки		6, 36, 66, 96, 126, 156	7, 37, 67, 97, 127, 157	8, 38, 68, 98, 128, 158	9, 39, 69, 99, 129, 159	10, 40, 70, 100, 130, 160
	16, 46, 76, 106, 136, 166	17, 47, 77, 107, 137, 167	18, 48, 78, 108, 138, 168	19, 49, 79, 109, 139, 169	20, 50, 80, 110, 140, 170
	26, 56, 86, 116, 146, 176	27, 57, 87, 117, 147, 177	28, 58, 88, 118, 148, 178	29, 59, 89, 119, 149, 179	30, 60, 90, 120, 150, 180
	15, 36, 75, 96, 126, 166	14, 35, 74, 95, 125, 167	13, 34, 73, 94, 124, 168	12, 33, 72, 93, 123, 169	11, 32, 71, 92, 122, 170
	5, 55, 65, 115, 145, 176	4, 56, 64, 116, 146, 177	3, 57, 63, 117, 147, 178	2, 58, 62, 118, 148, 179	1, 59, 61, 119, 149, 180
	25, 44, 85, 104, 134, 156	24, 45, 84, 105, 135, 157	23, 46, 83, 106, 136, 158	22, 47, 82, 107, 137, 159	21, 48, 81, 108, 138, 160
	7, 54, 67, 114, 144, 166	8, 55, 68, 115, 145, 167	9, 56, 69, 116, 146, 168	10, 57, 70, 117, 147, 169	11, 58, 71, 118, 148, 170
	17, 34, 77, 94, 124, 176	18, 35, 78, 95, 125, 177	19, 36, 79, 96, 124, 178	20, 37, 80, 97, 127, 179	21, 38, 81, 98, 128, 180
	27, 44, 87, 104, 134, 155	28, 45, 88, 105, 135, 154	29, 46, 89, 106, 136, 153	30, 47, 90, 107, 137, 152	1, 48, 61, 108, 138, 151
	10, 54, 70, 114, 144, 176	9, 55, 69, 115, 145, 177	8, 56, 68, 116, 146, 178	7, 57, 67, 117, 147, 179	6, 58, 66, 118, 148, 180

ТЕМА 1. МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрица. Основные понятия

Определение.Матрицей размера mхn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются латинскими буквами А, В, С, … и записываются в виде:

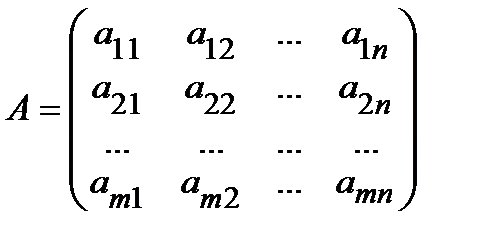
или в сокращенной записи: 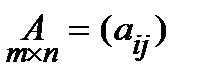, , 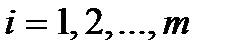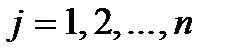. Каждый элемент 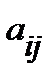матрицы имеет два индекса i и j, которые показывают, что элемент находится в i -ой строке и j -ом столбце.

Определение. Две матрицы А и В называются равными, если они имеют одинаковое число строк m и одинаковое число столбцов n и их соответствующие элементы равны: , , .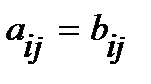

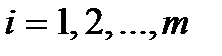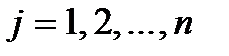Определение.Матрицей-строкой называется матрица, состоящая из одной строки:

.

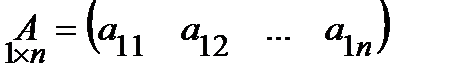Определение.Матрицей-столбцом называется матрица, состоящая из одного столбца:

.

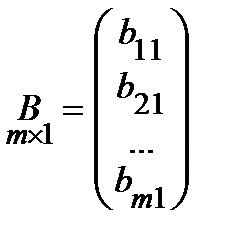Определение.Матрица, у которой число строк равно числу столбцов
(m = n), называется квадратной матрицей порядка n. Число строк или столбцов квадратной матрицы называется ее порядком.

Рассмотрим квадратную матрицу порядка n:

.

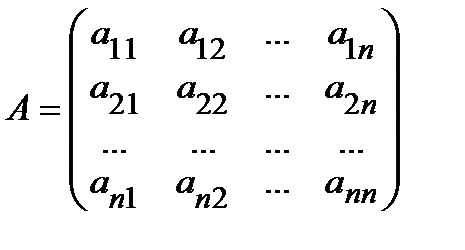Определение.Диагональ, содержащая элементы 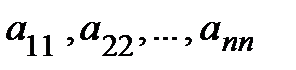, называется главной, а диагональ, содержащая элементы 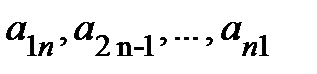, называется побочной (или вспомогательной).

Определение.Квадратные матрицы, у которых отличны от нуля только элементы, находящиеся на главной диагонали называются диагональными:

.

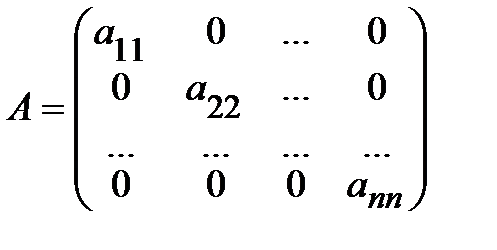Определение.Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка и обозначается:

.

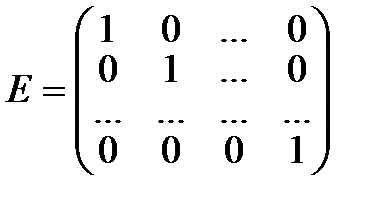Действия над матрицами

Умножение матрицы на число.

При умножении матрицы 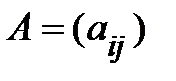на число 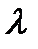каждый ее элемент умножается на это число .

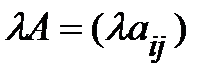Пример.

Дана матрица 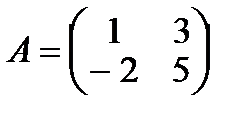, тогда .

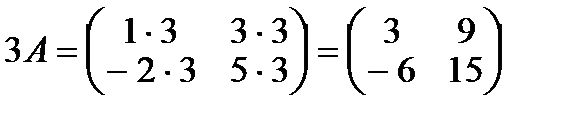Сложение матриц.

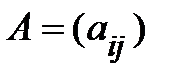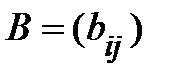Суммой двух матриц и одинакового размера mхn является матрица C размера mхn, элементы которой вычисляются по формуле 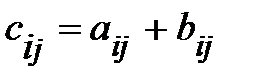для 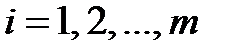, 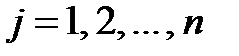(т.е. матрицы складываются поэлементно).

Пример.

Даны матрицы 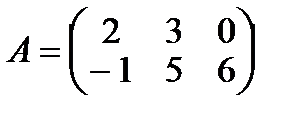и 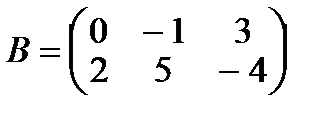, тогда матрица

.

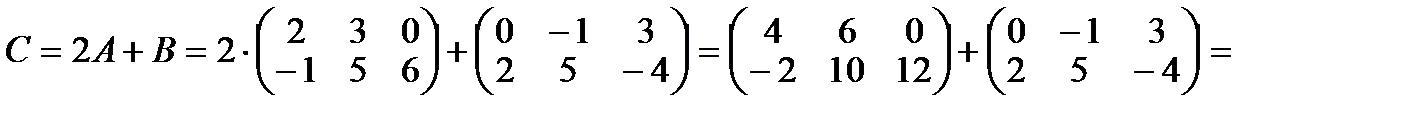
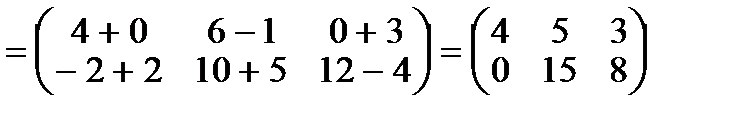Вычитание матриц.

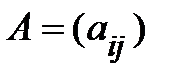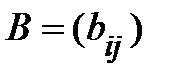Разностью матриц и одинакового размера mхn является матрица D размера mхn, элементы которой вычисляются по формуле 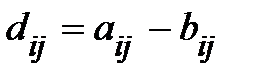для , .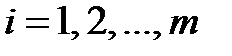

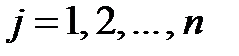Пример.

Даны матрицы 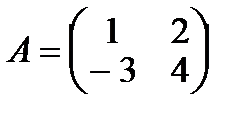и 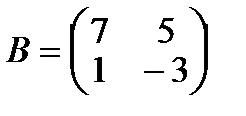, тогда матрица

.

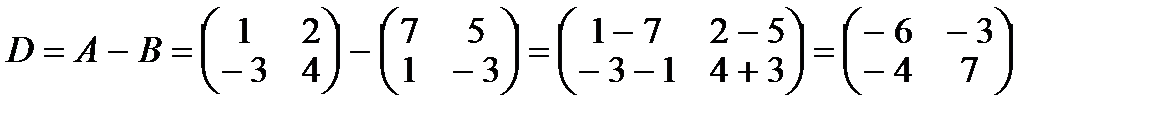Умножение матриц.

Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц 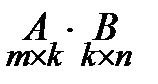называется такая матрица 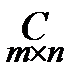, каждый элемент которой 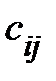равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B:

.

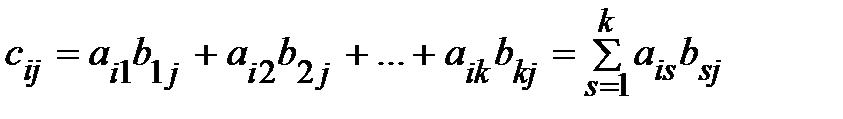Пример.

Даны матрицы 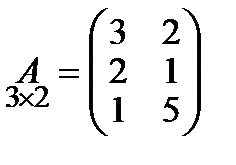и 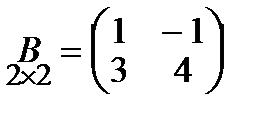, тогда

.

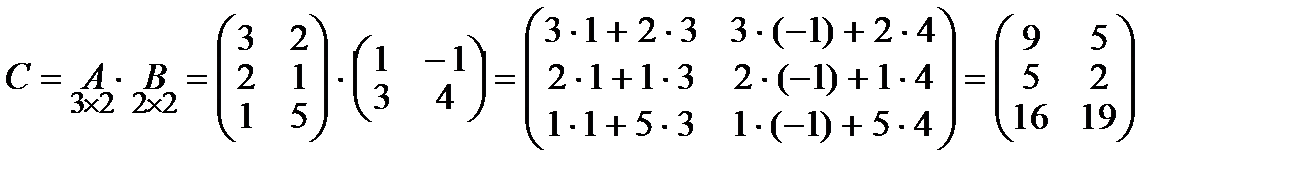Возведение в степень.

Целой положительной степенью 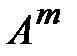(m > 1) квадратной матрицы A называется произведение m матриц, равных A, т.е.

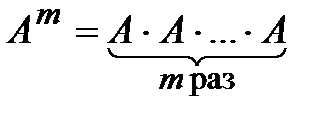. Операция возведения в степень определяется только для квадратных матриц.

Пример.

Дана матрица 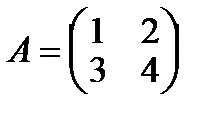, тогда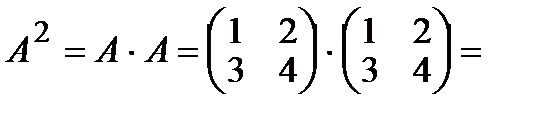

.

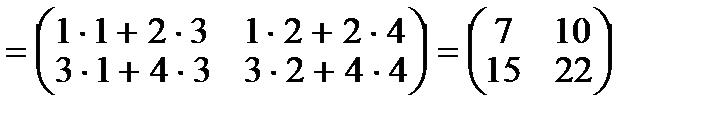Транспонирование матрицы.

Переход от матрицы A к матрице 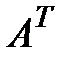, в которой строки и столбцы поменялись местами с сохранением порядка, называется транспонированием матрицы. Из определения следует, что если матрица A имеет размер mхn, то транспонированная матрица 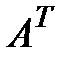имеет размер nхm.

Пример.

Дана матрица 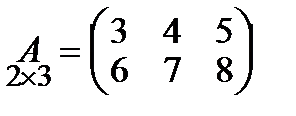, тогда .

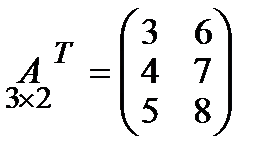Определитель. Основные понятия

Определение.Определителем называетсячисло, характеризующее квадратную матрицу А. Определитель обозначается 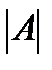или ∆ = det A (детерминант).

Определение.Определитель второго порядка матрицы 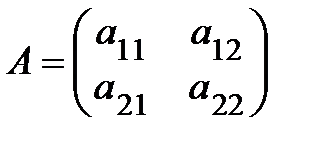вычисляется по формуле:

.

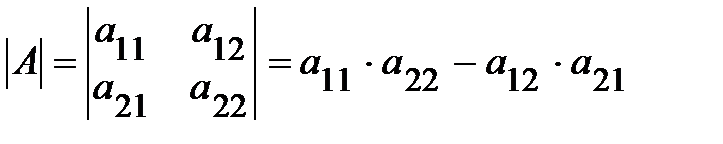Пример.

Дана матрица 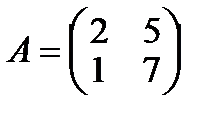, тогда .

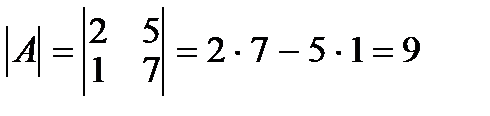Определение.Определитель третьего порядка матрицы 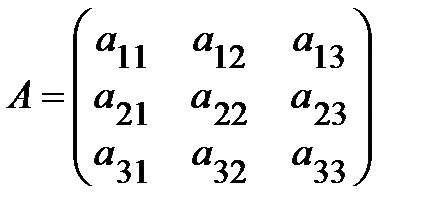вычисляется по формуле Саррюса («правило треугольников»:

.

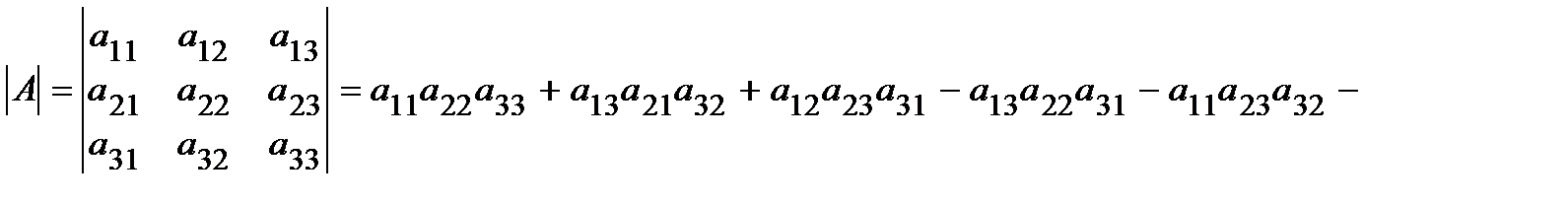
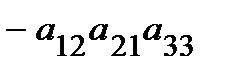Пример. Дана матрица 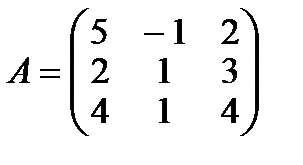, тогда

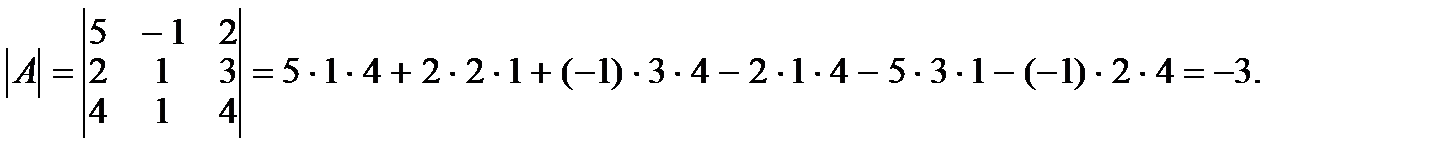
Определение.Минором 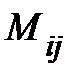элемента 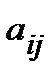определителя n-го порядка называется определитель (n – 1)-го порядка, полученный из данного определителя вычеркиванием i-ой строки и j-го столбца.

Определение.Алгебраическим дополнением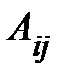элемента 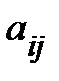определителя n-го порядка называется его минор, взятый со знаком :

.

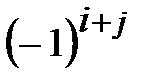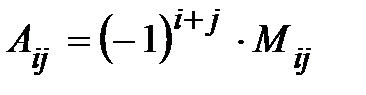Пример. Дана матрица .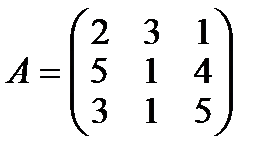

Минор 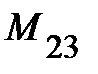элемента 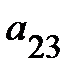получается из определителя матрицы A вычеркиванием второй строки и третьего столбца, т.е.

.

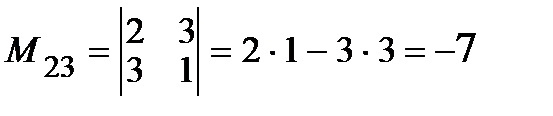Алгебраическое дополнение .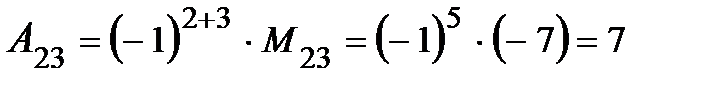

Обратная матрица

Определение. Матрица 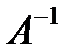называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

.

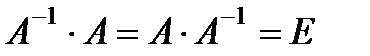Из определения следует, что только квадратнаяматрица имеет обратную. В этом случае и обратная матрица является квадратной того же порядка. Однако не каждая квадратная матрица имеет обратную.

Определение. Если определитель матрицы отличен от нуля 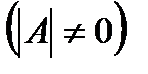, то такая квадратная матрица называется невырожденной, в противном случае 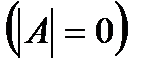– вырожденной.

Теорема 1 (Необходимое и достаточное условие существования обратной матрицы). Обратная матрица А^-1 существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.

Алгоритм вычисления обратной матрицы

1. Вычисляется определитель матрицы А. Если 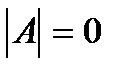, то матрица А – вырожденная и обратной матрицы 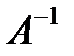не существует. Если 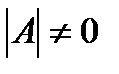, то матрица А – невырожденная и обратная матрица существует.

2. Вычисляются алгебраические дополнения всех элементов 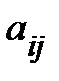матрицы А и записывают новую матрицу .

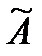3. Вычисляют матрицу 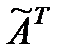, транспонированную к матрице .

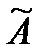4. Вычисляют обратную матрицу по формул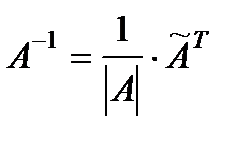е , где .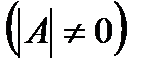

5. Проверяют правильность вычисления обратной матрицы 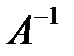, исходя из ее определения: .

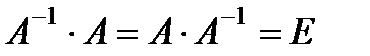Пример. Найти обратную матрицу для матрицы

.

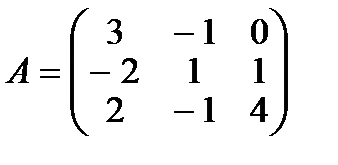Решение.

1. Вычисляем определитель матрицы A:

.

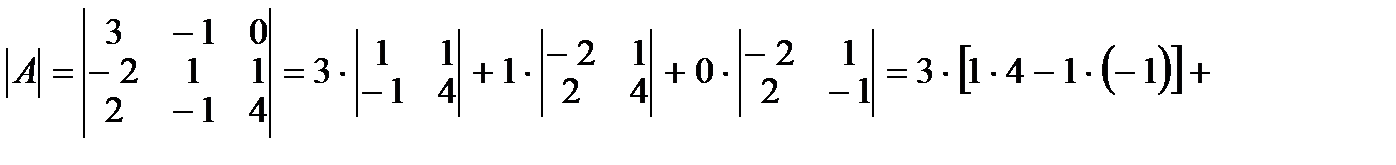
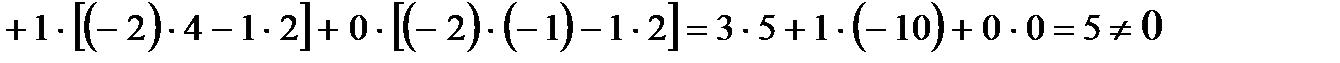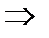матрица A – невырожденная и 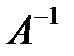существует.

2. Вычисляем алгебраические дополнения 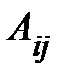элементов матрицы:

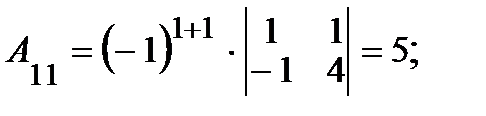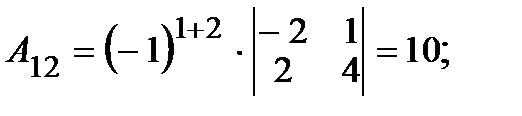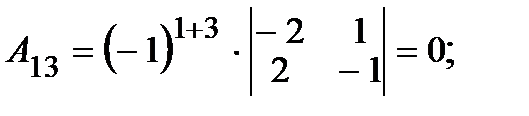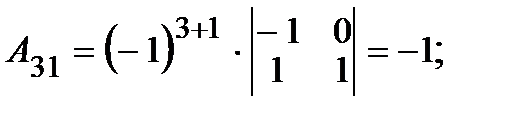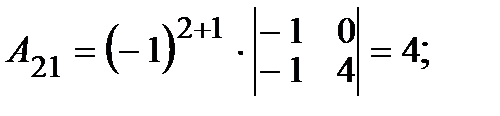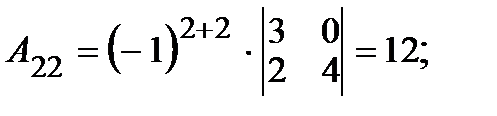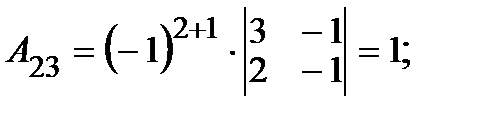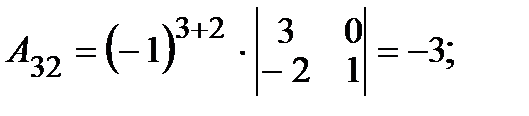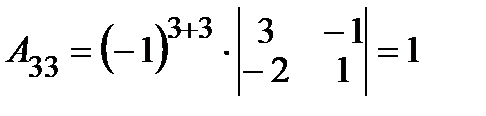.	Записываем матрицу .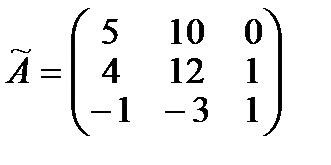

3. Матрица 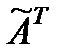, транспонированная к матрице 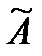, имеет вид:

.

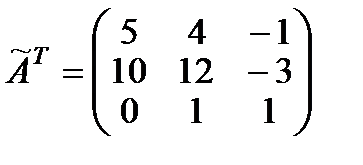4. Вычисляем обратную матрицу по формуле: .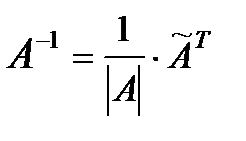

.

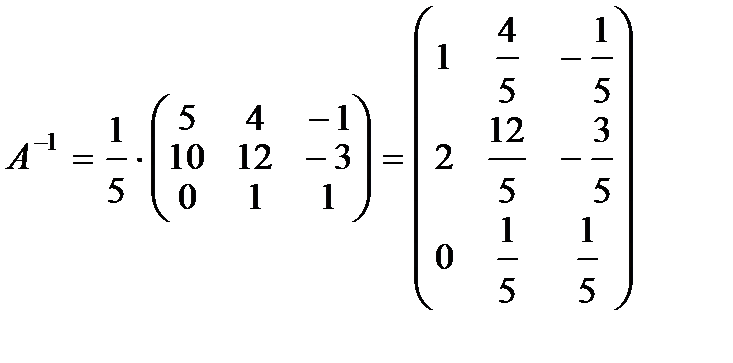5. Проверяем правильность вычисления обратной матрицы .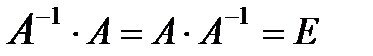

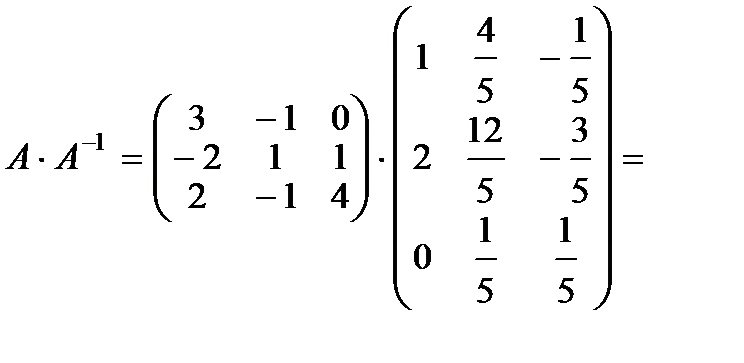
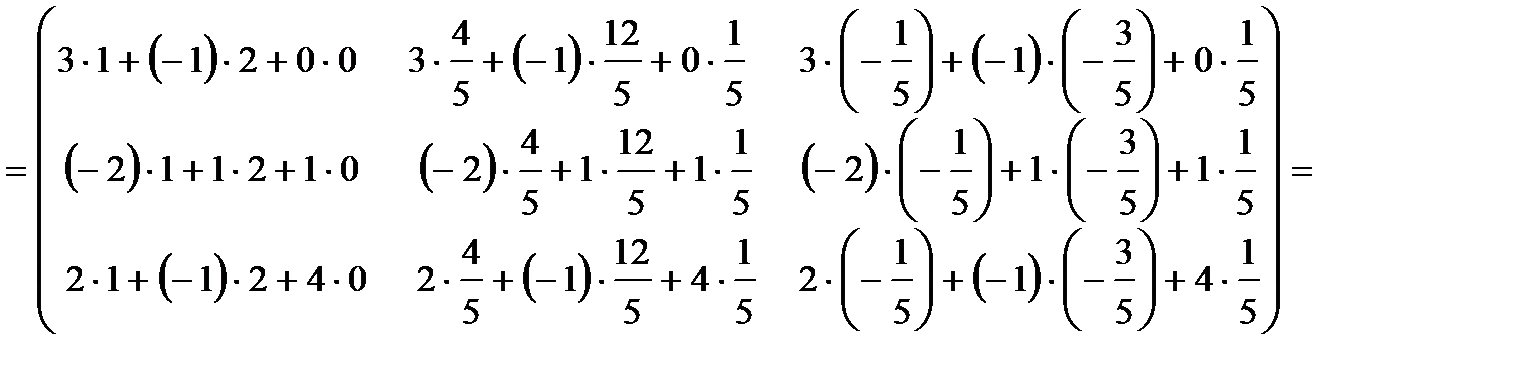
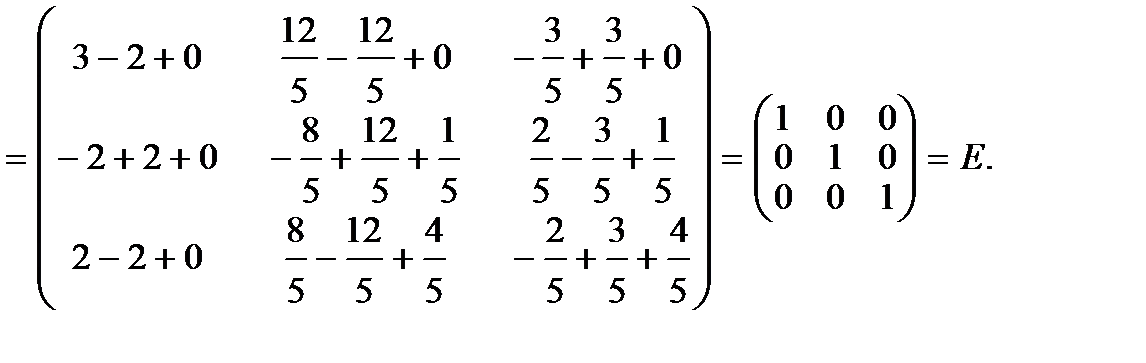
Следовательно, обратная матрица вычислена правильно.

Решение невырожденных линейных систем.