Б) Основные характеристики.

Рассмотрим основные характеристики функции:

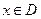1) Функция называется четной, если для любого выполняется условие 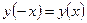( 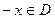). График четной функции симметричен относительно оси .

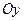Функция называется нечетной, если для любого 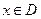выполняется условие 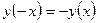. График нечетной функции симметричен относительно начала координат.

Например, 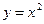– четная, т.к. ;

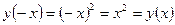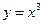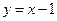– нечетная, т.к. , а – функция общего вида (т.е. ни четная, ни нечетная).

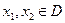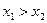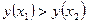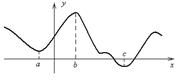
2) Функция называется возрастающей (неубывающей), если для любых таких, что выполняется неравенство ( 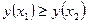) (т.е. большему значению аргумента соответствует большее значение функции). На график линия слева направо направлена снизу вверх.

Функция называется убывающей (невозрастающей), если для любых 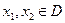таких, что 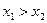выполняется неравенство 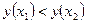( 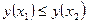) (т.е. большему значению аргумента соответствует меньшее значение функции). График идет сверху вниз.

Эти функции называются монотонными (а возрастающие и убывающие – строго монотонными). Интервалы, в которых функция монотонная называются интервалами монотонности.

3) Функция называется ограниченной, если существует такое число 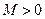, что для всех 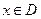выполняется неравенство 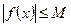. Следовательно, график функции лежит между прямым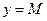и и .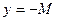

4) Функция называется периодической, если существует такое число 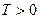, что для всех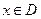 (если 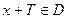). При этом число 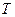называется периодом функции. Периодическими будут также числа 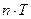( 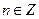); наименьшее положительное число, удовлетворяющее этому равенству считают основным периодом. График повторяет сам себя.

в) Обратная и сложная функции.

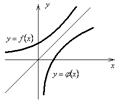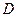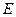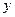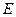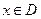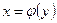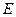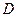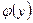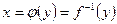Пусть задана функция с областью определения и множеством значений . Если любому значению , принадлежащему соответствует единственное значение , то определена функция с областью определения и множеством значений . Такая функция называется обратной к функции и записывается . Про функции и 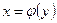говорят, что они являются взаимно обратными.

Например, для 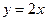обратной функцией будет .

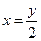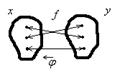
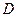Из определения обратной функции следует, что функция имеет обратную тогда и только тогда, когда соответствие между и 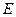взаимно однозначное, следовательно, любая строго монотонная функция имеет обратную (при этом если функция возрастает (убывает), то и обратная функция возрастает (убывает)). Заметим, что обратные функции изображаются одной и той же кривой, т.е. графики их совпадают. Если же условиться считать, что, как обычно, аргумент обозначается 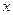, а зависимая переменная 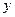, то обратная функция запишется в виде 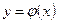, а графики взаимно обратных функций симметричны относительно биссектрисы 1 и 3 координатных углов (т.к. если точка 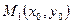принадлежит функции, то 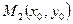принадлежит обратной функции, т.е. симметричны относительно прямой ).

Пусть функция 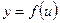определена на множестве 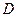, а функция 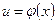в свою очередь на множестве 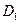(причем для любого 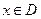, соответствующее значение 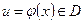). Тогда на множестве 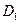определена функция 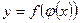, которая называется сложной функцией от 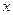(или функцией от функции). Переменную 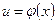называют промежуточным аргументом.

Например, 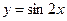. Здесь 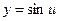, 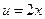. Сложная функция может иметь несколько промежуточных аргументов.