Интегрирование тригонометрических выражений R(sinx,cosx)непарных по sinx
Неопределенный интеграл
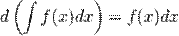
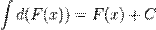
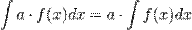
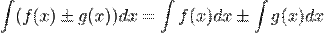
Если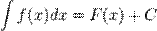 
, то и 
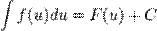, где 
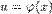— произвольная функция, имеющая непрерывную производную
Из определения интеграла следуют две важные формулы: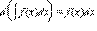 
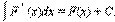
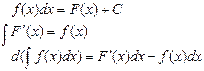
Интергирование по частям.Примеры
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
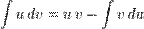
для определённого:
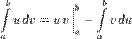
Для неопределённого интеграла
Функции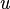 
и 
гладкие, следовательно, возможно дифференцирование:
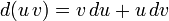
Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:
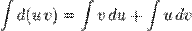
Операция интегрирования обратна дифференцированию:
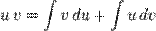
После перестановок:
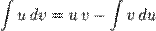
Примеры
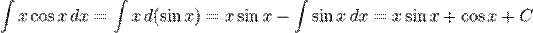
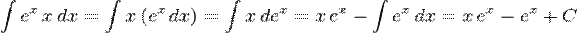
Таблица интегралов
5. Рациональные дроби,правильные,не правильные,примеры
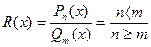прав,не прав
Непр.----выделяем целую часть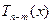 
+прав дробь(раскладываем на целую дробь)
Прав. Дробь----в знаменатели-раскладываем на множители--à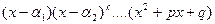 
Примеры:
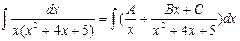
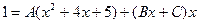
х=0
1=5А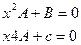 
В=1/5,С=-4А
Рациональные дроби.Разложение.Метод неопределенных коэффициентов.
Разложение дроби
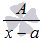
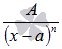
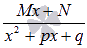
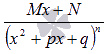
подынтегральной функции на простейшие дроби , все сводится к достаточно простым интегралам
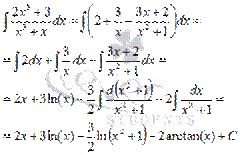
Метод неопределенных коэффициентов
Разложить дробь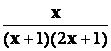 
на простейшие.
Решение: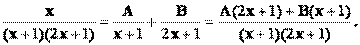 
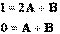
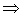
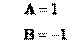
Комбинированный метод определения коэффициентов разложения рациональных дробей
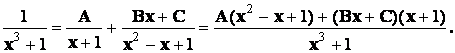
Найдем коэффициенты разложения комбинированным методом :
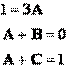
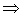
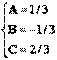
Таким образом,
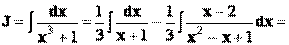
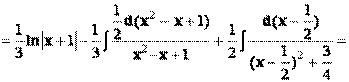
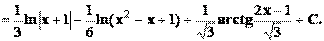
Интегрирование дробей 3 типа
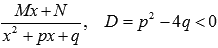
Для начала представляем неопределенный интеграл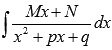 
в виде суммы:
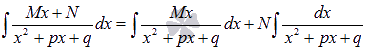
Первый интеграл берем методом подведения под знак дифференциала:
Поэтому,
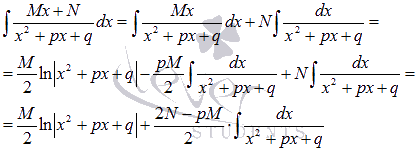
У полученного интеграла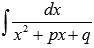 
преобразуем знаменатель:
Следовательно,
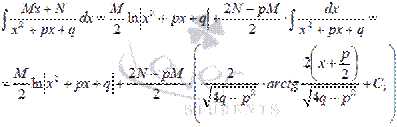
Формула интегрирования простейших дробей третьего типа принимает вид:
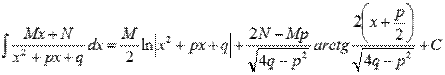
Пример.
Найдите неопределенный интеграл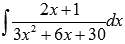 
.
Используем полученную формулу:
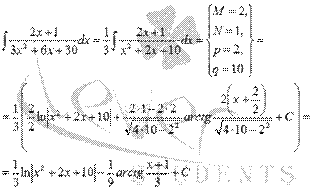
Если бы у нас не было этой формулы, то как бы мы поступили:
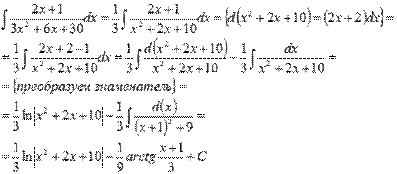
- Интегрирование простейших дробей четвертого типа
Первый шаг – подводим под знак дифференциала:
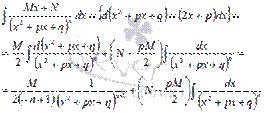
Второй шаг – нахождение интеграла вида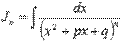 
. Интегралы подобного вида находятся с использованием рекуррентных формул
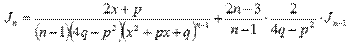
Интегрирование тригонометрических примеров
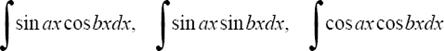
находятся с помощью тригонометрических формул
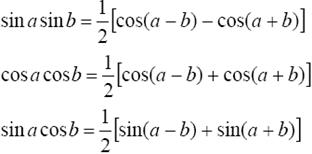
11..Интегрирование тригонометрических примеров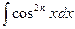 
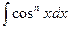n-нечетная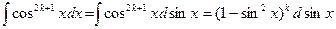 
Если n-четная--> понижаем степень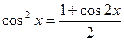 
|
Понижение степени
| |||||
|
Интегрирование тригонометрических выражений R(sinx,cosx)непарных по sinx
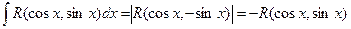
Специальные подстановки
1) Если R (-sin x, cos x) = -R (sin x, cos x), то рационализует подстановка cos x = t.
2) Если R (sin x, -cos x) = -R (sin x, cos x), то рационализует подстановка sin x = t.
3) Если R (-sin x, -cos x) = R (sin x, cos x), то рационализует подстановка tg x = t.