Задача 3. Расчет трехфазной, соединенной треугольником

Задача 1. Расчет разветвленной цепи постоянного тока

Задана эквивалентная схема замещения цепи постоянного тока и ее параметры (таблица 1). Выполнить следующие действия по ее расчету:

1. Составить систему расчетных уравнений для определения токов в ветвях схемы, используя оба закона Кирхгофа непосредственно (метод законов Кирхгофа);
2. Рассчитать токи в ветвях схемы, используя метод контурных токов;
3. Составить и проверить баланс мощностей.
4. Определить показания приборов.
5. На лабораторных работах смоделировать схему в программе WORK BEANCH и сравнить результаты.

Схема замещения цепей постоянного тока(для первого расчетного задания)

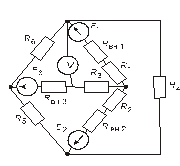
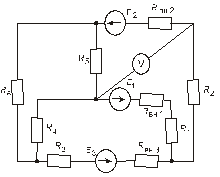
Рис. 1. Рис. 2.

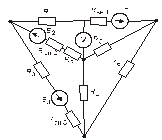
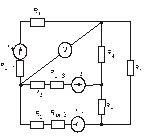
Рис. 3. Рис. 4.

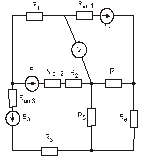
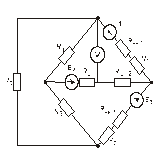
Рис. 5. Рис. 6.

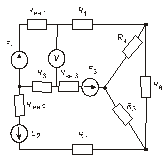
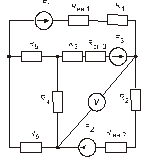
Рис. 7. Рис. 8.

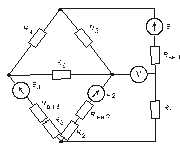
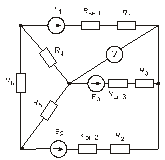
Рис. 9. Рис. 10.

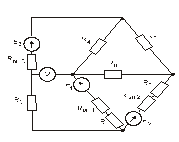
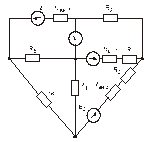
Рис. 11. Рис. 12.

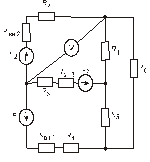
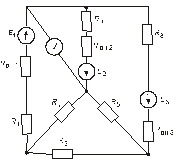
Рис. 13. Рис. 14.

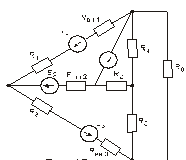
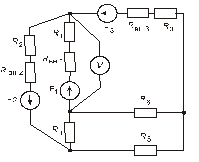
Рис. 15. Рис. 16.

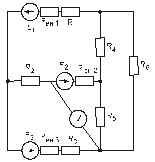
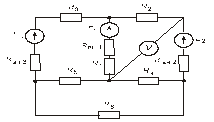
Рис. 17. Рис. 18.

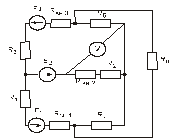
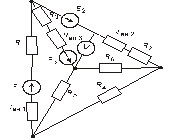
Рис. 19. Рис. 20.

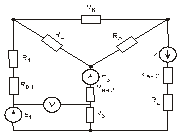
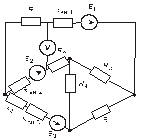
Рис. 21. Рис. 22.

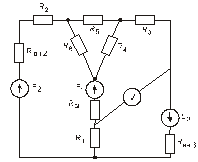
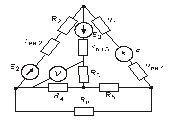
Рис. 23. Рис. 24.

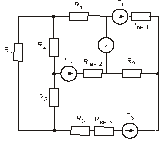
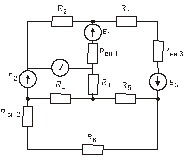
Рис. 25. Рис. 26.

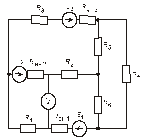
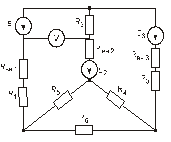
Рис. 27. Рис. 28.

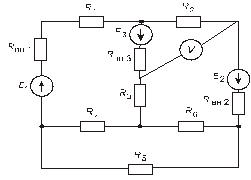
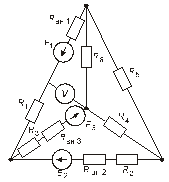
Рис. 29. Рис. 30.

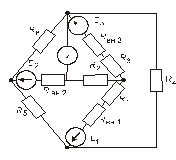
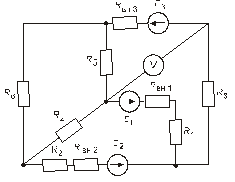
Рис. 31. Рис. 32.

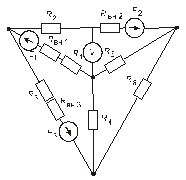
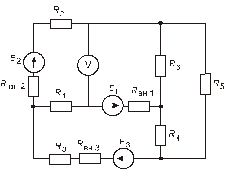
Рис. 33. Рис. 34.

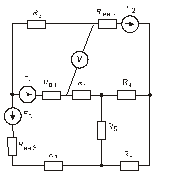
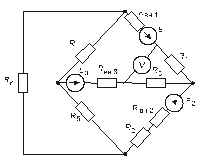
Рис. 35. Рис. 36.

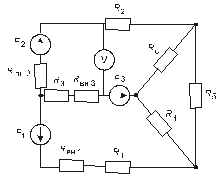
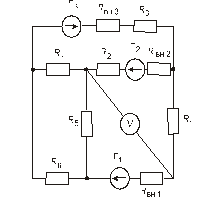
Рис. 37. Рис. 38.

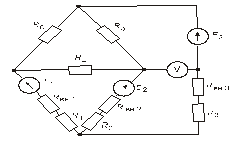
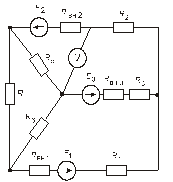
Рис. 39. Рис. 40.

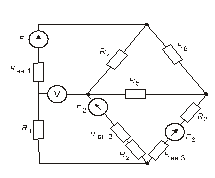
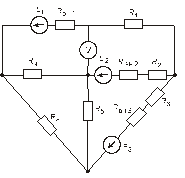
Рис. 41. Рис. 42.

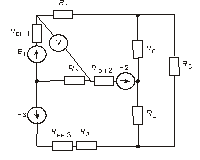
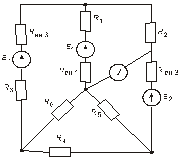
Рис. 43. Рис. 44.

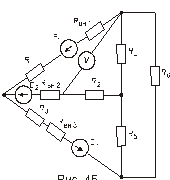
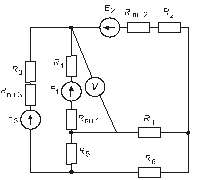
Рис. 45. Рис. 46.

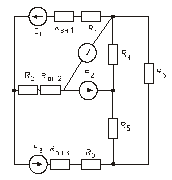
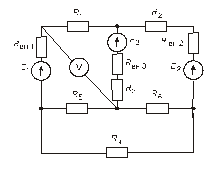
Рис. 47. Рис. 48.

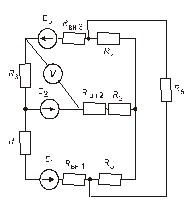
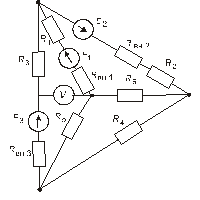
Рис. 49. Рис. 50.

Параметры схем замещения ( для первого расчетного задания)

Номер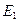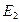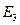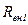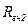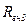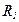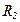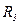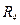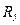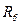
вариант	рисунок
-	-	В	В	В	Ом	ОМ	Ом	Ом	Ом	Ом	Ом	Ом	Ом
					0,1	0,3	0,4
					0,3	0,5	0,2
					0,3	0,1	0,2
					0,2	0,4	0,2
					0,5	0,4	0,3
					0,1	0,2	0,2
					0,3	0,4	0,5
					0,1	0,2	0,3
					0,4	0,2	0,3
					1,1	1,5	0,4	3,5	4,5	5,8	9,5	10,1
			7,4	6,5	0,2	0,3	0,4	5,5	6,5	4,5	8,5	7,5	9,5
					0,4	0,5	0,6
		0,5	0,7	0,9	0,1	0,2	0,3	1,2	1,7	1,5
					0,1	0,2	0,1
					0,2	0,3	0,4
					0,1	0,1	0,1
					0,2	0,4	0,6	1,2	1,5	2,5	4,2
		1,7	1,9	1,5	0,1	0,1	0,1	1,5	1,6	1,7	1,8	1,9
		2,5	2,5		0,2	0,2	0,2
					0,1	0,1	0,1	2,1	3,4	3,7	5,5	8,2	9,1
					0,1	0,2	0,3
					1,2	1,5	1,1
					0,2	0,5	0,7
					1,2	1,3	1,5
					0,4	0,5	0,6
					1,2	1,4	1,6	2,5	2,6	2,4	2,7	2,8	2,9
		0,5	0,7	0,9	0,1	0,1	0,1
					0,2	1,3	2,3
					0,1	0,2	0,3
					0,1	0,2	0,3
					1,1	1,2	1,3
					1,1	1,4	1,7
					0,5	0,6	0,7	1,9	1,8		2,3	2,5	2,4
					0,1	1,1	0,5
					0,1	0,2	1,1
					1,2	1,3	1,5
					1,1	1,2	1,3
					0,2	0,2	1,1
					1,1	1,5	1,6
					0,1	0,2	0,3
					0,2	0,3	0,4
					1,1	1,2	1,3
					1,2	1,3	1,5
					1,1	1,2	1,3
					0,1	0,2	0,5	2,3	2,1	2,5	3,1	2,8	2,9
					1,1	1,2	1,4
					0,1	0,2	0,3
					1,4	1,2	2,1
					0,2	0,4	0,6				2,1	2,5	2,8
		0,9	1,5	2,5
		-12	-8			0,2	0,3
				-45	0,1		0,3
		-4	-2		0,1	0,2	0,3
			-16		0,3	0,5	0,4
				-24		0,2	0,3					1,9	0,7
				-4	0,5		1,1
		-9			0,1	0,1						7,2	9,3
		-4	-8	-50		0,5	1,2
		-8	-4	-45	1,1	1,5	1,8
			-8		1,3		2,1
						1,2	2,3		4,2	3,5	4,6	7,8
			-8	-3	1,1	2,1	3,2		4,2	5,1	3,8	3,7
				-6	0,8	1,4	1,6		4,3	2,5	2,7
				-90	1,4	1,5	1,7
				-80		1,5	2,4
					0,7	1,5
					1,2	1,3	1,5
		-8	-4	-52		0,2	0,5
			-9	-4	0,2	0,3	0,4
			-8	-4	1,1	1,5	2,1
			-9	-4	1,1	0,3	0,2
			-9		2,3		1,1
			-5			2,5	1,5	4,2	5,1	6,3		7,8
			-5	-6	1,2		2,1	5,1	2,3	3,4
			-4	-50		0,2	0,3
			-5	-6	1,2	2,1	3,2
				-4		0,3	0,5
			-4		1,1	1,2	2,5
			-5		1,1	1,5	1,3
			-5	-6	2,1	1,3	1,4			7,2	5,6	9,3
				-90	1,8	2,8	0,2			3,2	2,7	4,1	5,5
						2,1	0,3					8,5	9,1
			-2	-8
					1,1	1,2	2,1
		-10			0,2	0,3	0,4
			-8		0,5	0,5	1,5
			-9	-5	0,1	0,2	1,5		6,2	5,4	3,7	4,9	5,8
				-16	1,2	0,2	0,8					7,2	5,1
		-4	1,8	-2,1		0,1	0,2	2,1	2,4	2,5	2,7	3,2	3,5
				-90	0,2	0,3	0,5	2,1	3,2	4,3
			-8	-4	0,1	0,5	1,1
						0,5	0,5
				-15	0,1	0,2	0,3
		-5				1,3	1,5			4,5	5,1	2,3	3,6
					0,3	0,2	0,2	3,2	3,3	3,4	3,5	3,6	3,7
			-8		0,1	0,2	0,3	2,3	2,5	2,7	2,9	3,1	3,3
				-50	1,1	1,2	1,3
			-8			0,2	1,2	4,2	4,3	4,1	3,2	2,1	2,5
		1,7	-2	-15		0,1	0,2	1,2	1,3	1,4	1,5	1,6	1,7
				-5	1,2	1,5	1,9

Задача 2. Расчет последовательной цепи синусоидального тока

В цепи, схема которой приведена на рис. 19, требуется:

1. Определить: действующее I и амплитудноеI_m значения тока; действующие значения напряжений на элементах цепи U_R , U_L , U_C ; действующее U и амплитудное U_m значения напряжения на зажимах цепи; угловую частоту ω; угол сдвига фаз между напряжением и током φ; начальную фазу напряжения на зажимах цепи ψ_u; мощности элементов цепи Р , Q_L , Q_C ; полную S и реактивную Q мощности цепи; коэффициент мощности цепи cosφ. Одна из этих величин может оказаться заданной.
2. Составить уравнения мгновенных значений тока i(ωt) и напряжения u(ωt) и построить синусоиды, соответствующие этим уравнениям.
3. Построить векторную диаграмму тока I и напряжений U_R , U_L , U_C и треугольник мощностей. Исходные данные к расчету приведены в табл. 11 и 12. Частота f = 50 Гц.

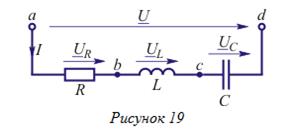
Таблица 11

Номер личного варианта	R, Ом	L, мГн	C, мкФ	ψi, град	Номер личного варианта	R,Ом	L, мГн	C, мкФ	ψi , град
1	2	3	4	5	6	7	8	9	10
1, 26,51,76 2, 27,52,77 3,28,53,78 4,29,54,79 5,30,55,80 6,31,56,81 7,32,57,82 8,33,58,83 9,34,59,84 10,35,60,85 11,36,61,86 12,37,62,87 13,38,63,88		9,6 12,7 9,6 12,7 19,1 6,4 19,1 6,4 6,4 12,7 12,7 9,6 19,1		-90 -80 -70 -60 -50 -40	14,39,64,89 15,40,65,90 16,41,66,91 17,42,67,92 18,43,68,93 19,44,69,94 20,45,70,95 21,46,71,96 22,47,72,97 23,48,73,98 24,49,74,99 25,50,75,100		15,9 6,4 6,4 19,1 15,9 9,6 15,9 9,6 9,6 15,9 19,1 22,3		-30 -20 -10 -45 -35

Таблица 12

Последняя цифра варианта	1,6	2,7	3,8	4,9	5,0
Дано	U = 12 В	S = 100 В*А	Q = 72 вар	Uac = 10 В	Ubc = 4 В

Задача 3. Расчет трехфазной, соединенной треугольником

Комплексные сопротивления фаз приемника определяются выражениями: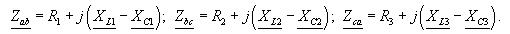

Числовые значения R₁ , X_L1 , … , X_C3 даны в табл. 16. Значение линейного напряжения сети U_Л , к которой подключен приемник, приведено в табл. 17

Начертить схему цепи и показать на ней условно положительные направления линейных напряжений, линейных и фазных токов. (Элементы цепи, сопротивления которых равны нулю, на схеме не показывать).

Определить: фазные I_ab , I_bc , I_caи линейные I_a , I_b , I_c; токи углы сдвига фаз между фазными напряжениями и токами φ_ab , φ_bc, φ_ca.

Построить векторную диаграмму напряжений и токов.

Таблица 16

Номер личного варианта	Сопротивления, Ом
R1	XL1	XC1	R2	XL2	XC2	R3	XL3	XC3
1	2	3	4	5	6	7	8	9	10
1,26,51,76 2,27,52,77 3,28,53,78, 4,29,54,79 5,30,55,80 6,31,56,81 7,32,57,82 8,33,58,83 9,34,59,84 10,35,60,85 11,36,61,86 12,37,62,87 13,38,63,88 14,39,64,89 15,40,65,90 16,41,66,91 17,42,67,92 18,43,68,93 19,44,69,94 20,45,70,95 21,46,71,96 22,47,72,97 23,48,73,98 24,49,74,99 25,50,75,100

Таблица 17

Последняя цифра варианта	1,6	2,7	3,8	4,9	5,0
Линейное напряжение сети, В