Критерии достоверности различия фактического и теоретического распределений

6.1 Критерий Пирсона

χ² = ∑((n − ň)² / ň), (6.1)

где n − фактическая численность;

ň − теоретическая численность.

Таблица 6.1 Вычисление меры совпадения фактического и теоретического вариационных рядов (по Пирсону) для диаметра

диаметр xj, см	численность, шт	nj- ňj	(nj- ňj)2	χ2= (nj- ňj)2/ ňj
фактическая nj	теоретическая ňj
≤ 11,0		6,6	3,4	11,56	1,75
13,0		6,8	3,2	10,24	1,51
15,0		11,6	-5,6	31,36	2,70
17,0		17,0	-3,0	9,00	0,53

Продолжение таблицы 6.1

19,0		22,4	-3,4	11,56	0,52
21,0		26,2	1,8	3,24	0,12
23,0		27,2	8,8	77,44	2,85
25,0		25,2	-0,2	0,04
27,0		20,8	-5,8	33,64	1,62
29,0		15,2	-1,2	1,44	0,10
31,0		10,0	3,0	9,00	0,90
33,0		5,8	-0,8	0,64	0,11
≥35,0		5,2	-0,2	0,04	0,01
всего				─	12,84

χ² = 12,84

U' = k − q, (6.2)

где k − число образованных интервалов (классов);

q − число ограничений.

k = 13

q = 3

U = 13 − 3 = 10

χ²_st = 18,3 для I уровня надежности

χ² < χ²_st

Опытное распределение можно считать нормальным, а отличие его от теоретического является случайным.

Таблица 6.2 Вычисление меры совпадения фактического и теоретического вариационных рядов (по Пирсону) для высоты

высота yj, м	численность, шт	nj- ňj	(nj- ňj)2	χ2= (nj- ňj)2/ ňj
фактическая nj	теоретическая ňj
≤ 14,0		7,6	4,4	19,36	2,55
16,0		14,2	-4,2	17,64	1,24
18,0		27,6	-5,6	31,36	1,14
20,0		39,8	-7,8	60,84	1,53
22,0		43,0	2,0	4,00	0,09
24,0		34,4	14,6	213,16	6,20
≥26,0		33,2	-3,2	10,24	0,31
всего				─	13,06

χ² = 13,06

k = 7

q = 3

U = 7 − 3 = 4

χ²_st = 9,5 для I уровня надежности

χ²_st = 13,3 для II уровня надежности

χ² > χ²₁

Отличие опытного распределения от нормального доказано для I уровня надежности.

6.2 Критерий Колмогорова и Смирнова

Таблица 6.3 Вычисление критерия λ (по диаметру)

диаметр xj, см	численность, шт.	накопленная численность, шт.	∑n - ∑ň
фактическая n	теоретическая ň	фактическая ∑n	теоретическая ∑ň
5,0	─	0,2	─	0,2	0,2
7,0	─	0,8	─	1,0	1,0
9,0		1,8		2,8	1,8
11,0		3,8		6,6	3,4
13,0		6,8		13,4	6,6
15,0		11,6		25,0	1,0
17,0		17,0		42,0	2,0
19,0		22,4		64,4	5,4
21,0		26,2		90,6	3,6
23,0		27,2		117,8	5,2
25,0		25,2		143,0	5,0
27,0		20,8		163,8	0,8
29,0		15,2		179,0	2,0
31,0		10,0		189,0	1,0
33,0		5,8		194,8	0,2
35,0		3,0		197,8	1,8
37,0		1,4		199,2	0,8
39,0	─	0,6		199,8	0,2
41,0	─	0,2		200,0
всего			─	─	─

Примечание. Максимальная разность накопленных численностей заключена в рамку.

λ = [ ∑n − ∑ň ]max / √N, (6.3)

где [ ∑n − ∑ň ]max − максимальная разность между накопленными фактическими и теоретическими численностями одного и того же класса;

N − общая численность фактического распределения.

λ = 6,6 / √200 = 0,47

Эмпирический критерий λ меньше стандартного (0,48 < 1,36). Различие фактического и теоретического рядов по Гауссу-Лапласу недостоверно.

Таблица 6.4 Вычисление критерия λ (по высоте)

высота yj, м	численность, шт.	накопленная численность, шт.	∑n - ∑ň
фактическая n	теоретическая ň	фактическая ∑n	теоретическая ∑ň
8,0		0,2		0,2	0,8
10,0		0,4		0,6	1,4
12,0		1,6		2,2	3,8
14,0		5,4		7,6	4,4
16,0		14,2		21,8	0,2
18,0		27,6		49,4	5,4
20,0		39,8		89,2	13,2
22,0		43,0		132,2	11,2
24,0		34,4		166,6	3,4
26,0		20,4		187,0	9,0
28,0		9,0		196,0	3,0
30,0		3,0		199,0	1,0
32,0	─	0,8		199,8	0,2
34,0	─	0,2
всего			─	─	─

Примечание. Максимальная разность накопленных численностей заключена в рамку.

λ = 13,2 / √200 = 0,93

Эмпирический критерий λ меньше стандартного (0,93 < 1,36). Различие фактического и теоретического рядов по Гауссу-Лапласу недостоверно.

ПОКАЗАТЕЛИ МЕРЫ СВЯЗИ ВЗАИМОЗАВИСИМЫХ СТАТИСТИЧЕСКИХ ВЕЛИЧИН

7.1 Вычисление коэффициента корреляции, корреляционного отношения и других численных характеристик корреляционной таблицы

Таблица 7.1 Вычисление коэффициента корреляции r и корреляционного отношения η

диаметр х, см	высота y, м	номер столбца
												1 nx	2 kx	3 nxkx	4 nxkx2	5 ∑ nxyky	6 ∑ nxykykx	7 (∑ nxyky)2	8 (∑ nxyky)2/ nx
														-7	-7		-7			49,0
														-6	-54		-39			169,0
														-5	-50		-33			108,9
														-4	-24		-14			32,7
														-3	-42		-19			25,8
														-2	-38		-32			53,9
														-1	-28		-9			2,9
																				3,4
																				6,8
																				15,0
																				25,8
																				48,1
																				24,2
																				25,0

Продолжение таблицы 7.1

(1) ny														-	-35		-49		-	590,5
(2 ) ky	-7	-6	-5	-4	-3	-2	-1						-
(3) nyky	-7	-6	-20	-24	-30	-44	-32						-49
(4) nyky2
(5) ∑ nxykx	-7	-6	-24	-31	-45	-61	-46						-35
(6) ∑ nxykxky
(7) (∑ nxykx)2													-
(8) (∑ nxykx)2/ ny	49,0	36,0	144,0	160,2	202,5	169,1	66,1		97,2	361,9	48,0	49,0	1383,0

7.1.1 Коэффициент корреляции

r = µ1/1 / σ'xσ'y, (7.1)

где µ1/1 − первый центральный момент произведения двух статистических величин;

σ'xσ'y − неименованные средние квадратичные отклонения статистических величин x, y.

µ1/1 = m1/1 − m1xm1y, (7.2)

где m1/ 1 − первый начальный момент произведения двух статистических величин;

m1x, m1y − первые начальные моменты статистических величин x, y.

m _1/1= ∑n_xyk_yk_x / ∑n, (7.3)

где ∑nxykykx − сумма произведений отклонений на численности;

∑n − общая численность выборки.

m _1/1= 959 / 200 = 4,795

μ _1/1 = 4,795 − (-0,175 ∙ (-0,245)) = 4,752

r = 4,752 / 2,93 ∙ 1,84 = +0,88

m_r = ±(1 − r²) / √∑n (7.4)

m_r = ±(1 − 0,88²) / √200 = ±0,016

r ± m_r = 0,88 ± 0,016

t₁ = r / mr = 0,88 / 0,016 = 55

Величина коэффициента корреляции достоверна. Теснота связи между диаметром и высотой высокая.

7.1.2 Корреляционное отношение

η² _y/x = 1 / μ_2y[1 / ∑n ∙ ∑((∑n_xyk_y)² / n_x ) − m_1y²], (7.5)

где µ2y − второй центральный момент по высоте, µ2y = 3,375;

∑n − общая численность выборки, ∑n = 200;

∑((∑nxyky)² / nx) − итоговые данные столбца 8 (см. табл. 7.1), равны 590,5;

m1y − первый начальный момент по высоте, m1y = -0,245.

η² _y/x = 1 / 3,375 [1 / 200 ∙ 590,5 − (-0,245)²] = 0,857

η _y/x = √0,857 = 0,93

m_η = ±(1 − η²) / √∑n, (7.6)

где mη − основная ошибка корреляционного отношения.

m_η = ±(1 − 0,93²) / √200 = ±0,010

η ± m_η = 0,93 ± 0,010

t₁ = 0,93 / 0,010 = 93

Величина корреляционного отношения достоверна.

7.1.3 Коэффициент (индекс) детерминации

Д = η²

Д = 0,93² = 0,87

7.1.4 Мера линейности

ξ = η² − r² (7.7)

ξ = 0,93² − 0,88² = 0,10

m_ζ ≈ ±√(ξ / ∑n) (7.8)

m_ζ ≈ ±√(0,10 / 200) = ±0,0557

ξ / m_ζ = 0,10 / 0,0557 = 1,80

Вероятность правильности вывода о криволинейности 0,90.

7.1.5 Показатель криволинейности

Kp = (η² − r²) / (1 − r²) (7.9)

Kp = (0,93² − 0,88²) / (1 − 0,88²) = 0,44

7.2 Вычисление коэффициента корреляции и корреляционного отношения малой выборки

Таблица 7.2 Вычисление коэффициента корреляции для малой выборки

№ п/ п	признак	центральное отклонение
xj	yj	xj- Mx= α	yj- My= β	αβ	α2	β2
	21,8	21,6	-2,0	-0,8	1,6	4,00	0,64
	28,5	27,0	4,7	4,6	21,62	22,09	21,16
	22,3	23,4	-1,5	1,0	-1,50	2,25	1,00
	18,0	16,7	-5,8	-5,7	33,06	33,64	32,49
	23,0	22,5	-0,8	0,1	-0,08	0,64	0,01
	23,5	23,0	-0,3	0,6	-0,18	0,09	0,36
	36,0	29,5	12,2	7,1	86,62	148,84	50,41
	19,0	17,8	-4,8	-4,6	22,08	23,04	21,16
	21,5	22,4	-2,3			5,29
	22,0	23,8	-1,8	1,4	-2,52	3,24	1,96
	13,0	16,4	-10,8	-6,0	64,80	116,64	36,00
	29,5	26,4	5,7	4,0	22,80	32,49	16,00
	22,5	19,1	-1,3	-3,3	4,29	1,69	10,89
	19,5	18,0	-4,3	-4,4	18,92	18,49	19,36
	28,0	24,5	4,2	2,1	8,82	17,64	4,41
	20,0	20,5	-3,8	-1,9	7,22	14,44	3,61
	30,0	25,0	6,2	2,6	16,12	38,44	6,76
	22,5	23,7	-1,3	1,3	-1,69	1,69	1,69
	27,0	24,0	3,2	1,6	5,12	10,24	2,56
	28,0	23,1	4,2	0,7	2,94	17,64	0,49
всего	475,6	448,4	-0,4	+0,1	310,04	512,52	230,96

M_x = 23,8 см., M_y = 22,4 м.

r = ∑αβ / √ ∑α²β², (7.10)

где α − центральное отклонение по диаметру;

β − центральное отклонение по высоте.

r = 310,04 / √ 512,52 ∙ 230,96 = 0,90

m_r = ±(1 − r²) / √∑n

m_r = ±(1 − 0,90²) / √20 = ±0,043

r ± m_r = 0,90 ± 0,043

t₁ = 0,90 / 0,043 = 21

Величина коэффициента корреляции достоверна. Теснота связи между диаметром и высотой высокая.

РЕГРЕССИОННЫЙ АНАЛИЗ

H = (h₁n₁ + h₂n₂ + h₃n₃ + .. + h_kn_k) / n₁ + n₂ + n₃ + .. + n_{k (8.1)}

Таблица 8.1 Опытные средние высоты по ступеням толщины

диаметр, см
опытная средняя высота, м	8,0	13,3	15,4	17,3	19,3	18,6	21,4	22,6	23,0	24,0	24,7	25,9	26,4	22,0	27,0

8.1 Вычисление уравнения прямой y = a + bx

Таблица8.2 Вычисление уравнения прямой y = a + bx

диаметр х, см	высота y, м	x2	xy	высота по уравнению(8.3) ỹ, м	(y −ỹ)2
	8,0		72,0	13,0	25,00
	13,3		146,3	14,1	0,64
	15,4		200,2	15,2	0,04
	17,3		259,5	16,3	1,00
	19,3		328,1	17,3	4,00
	18,6		353,4	18,4	0,04
	21,4		449,4	19,5	0,91
	22,6		519,8	20,6	4,00
	23,0		575,0	21,7	1,69
	24,0		648,0	22,8	1,44
	24,7		716,3	23,9	0,64
	25,9		802,9	24,9	1,00
	26,4		871,2	26,0	0,16
	22,0		770,0	27,1	26,01
	27,0		999,0	28,2	1,44
всего 345	308,9		7711,1	─	68,01

308,9= 15a+ 345b

{

7711,1= 345a+ 9055b

20,593= a+ 23,000b

{

22,351= a+ 26,246b

_22,351= a+ 26,246b

20,593= a+ 23,000b

1,758= 3,246b

b= 0,542

20,593 = a + 23,000b

20,593 = a + 23,000 ∙ 0,542

20,593= a+ 12,466

a= 20,593- 12,466

a= 8,127

ỹ = 8,127+ 0,542x (8.2)

m_y= ±√∑(y − ỹ)² / n − e (8.3)

m_y= ±√68,01 / 15 − 2 = ±2,29м

8.2 Вычисление уравнения параболы второго порядка y = a + bx + cx²

Таблица 8.3 Вычисление уравнения параболы второго порядка y= a+ bx+cx²

диаметр х, см	высота y, м	x2	x3	x4	xy	x2y	высота по уравнению ỹ, м	(y- ỹ)2
	8,0				72,0	648,0	9,8	3,24
	13,3				146,3	1609,3	12,3	1,00
	15,4				200,2	2602,6	14,5	0,81
	17,3				259,5	3892,5	16,5	0,64
	19,3				328,1	5577,7	18,4	0,81
	18,6				353,4	6714,6	20,0	1,96
	21,4				449,4	9437,4	21,4
	22,6				519,8	11955,4	22,6
	23,0				575,0	14375,0	23,6	0,36
	24,0				648,0	17496,0	24,3	0,09
	24,7				716,3	20772,7	24,9	0,04
	25,9				802,9	24889,9	25,2	0,49
	26,4				871,2	28749,6	25,3	1,21
	22,0				770,0	26950,0	25,3	10,89
	27,0				999,0	36963,0	25,0	4,00
всего 345	308,9				7711,1	212633,7	─	25,54

308,9= 15a+ 345b+ 9055c

{7711,1= 345a+ 9055b+ 259785c

212633,7= 9055a+ 259785b+ 7902127c

20,593= a+ 23b+ 603,667c

{22,351= a+ 26,246b+ 753c

23,483= a+ 28,690b+ 872,681c

_23,483= a+ 28,690b+ 872,681c

20,593= a+ 23b+ 603,667c

------------------------------------

2,890= 5,69b+ 269,014c

_23,483= a+ 28,690b+ 872,681c

22,351= a+ 26,246b+ 753c

-----------------------------------------

1,132= 2,444b+ 119,681c

2,890= 5,69b+ 269,014c

{

1,132= 2,444b+ 119,681c

0,508= b+ 47,278c

{

0,463= b+ 48,969c

_0,463= b+ 48,969c

0,508= b+ 47,278c

-0,045= 1,691c

c= -0,02661

0,508= b+ 47,278c

b= 0,508- 47,278c

b= 1,766

20,593= a+ 23b+ 603,667c

a= 20,593- 23b- 603,667c

a= -3,961

ỹ = -3,961 + 1,766x - 0,02661x² (8.4)

m_y = ±√∑(y− ỹ)² / n − e

m_y = ±√25,54 / 13 = ±1,40м.

8.3 Выбор оптимального уравнения

Таблица 8.4 Основные ошибки уравнений

вид уравнения	сумма квадратов отклонений	ошибка уравнения
уравнение прямой y = 8,127+ 0,542x	68,01	2,29
уравнение параболы второго порядка y = -3,961 + 1,766x − 0,02661x2	25,54	1,40

Лучшие результаты выравнивания высот по ступеням толщины дает уравнение параболы второго порядка y = -3,961 + 1,766x − 0,02661x².

h = -3,961 + 1,766d − 0,02661d² (8.5)

m_h = ±1,40м.

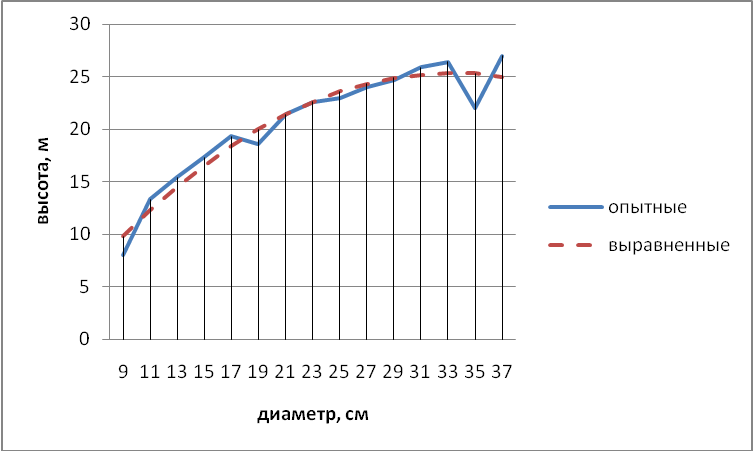
Рисунок 8.1 Кривые высот