О построении графов связи физических систем и получении математического описания их функционирования

Граф связи строится по схеме системы в соответствии с определенным алгоритмом. Для механических, электрических и гидравли­ческих систем этот алгоритм известен. Для механических систем, например, он предусматривает следующие про­цедуры:

1. Для каждой отдельной скорости установить 1-узел.

2. Включить соответствующие двух- и трёх- связные элементы между парами 1-узлов.

3. Включить накапливающие и рассеивающие элементы.

4. Задать направление мощностей.

5. Исключить 1-узлы, соответствующие нулевым скоростям, вместе с их связями.

6. Задать причинность на источниках усилия и потока и рас­пространить ее как можно дальше по графу.

7. Задать интегральную причинность на накапливающих эле­ментах и распространить ее как можно дальше по графу.

8. Задать причинность элементов графа, на которые не уда­лось распространить причинность, определяемую источниками и на­капливающими элементами.

Так, для системы, схема которой приведена на рис.3.1, граф связи без указания причинности дан на рис.3.2а и с указанием причинности – на рис.3.2б.

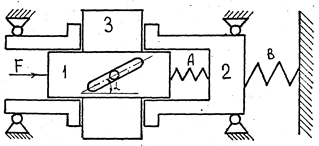
Рис. 3.1

а)

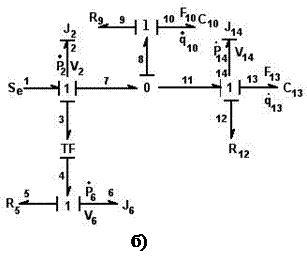
Рис 3.2

На рис 3.2б обозначено:

J₂, J₆, J₁₄ – накапливающие элементы, отражающие инер­ционность тел 1,3,2 соответственно. Их характеристика определена уравнением 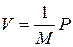; C₁₀, C₁₃ – накап­ливающие элементы, отражающие емкостные свойства пружин А и В. Их характеристика определена уравнением F = h×q; R₅, R₉, R₁₂ – рассеивающие элементы, отражающие трение при перемещении тел 3, 1, 2 соответственно. Их характери­стика определена уравнением F = hV; TF – элемент, преобразующий с коэффициентом r = tg a горизонтальное перемещение тела 1 в вертикальное тела 3.

Процесс получения математического описания по графу связи формализован. Он заключается в выполнении следующих операций:

1. Выделяются элементы, накапливающие энергию.

2. Анализируется причинность накапливающих элементов, которая определяет число дифференциальных уравнений, описывающих систему.

3. Для накапливающих элементов с интегральной причинностью вводятся переменные энергии.

4. По графу связи в соответствии с указанной на нем при­чинностью устанавливается связь каждой переменной энергии с дру­гими и входными воздействиями.

Для рассматриваемого примера:

1. Переменная P₂.

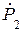– выход 1-узла по усилию; вход в этот узел по усилию идет по связям 1, 3, 7. Поэтому

.

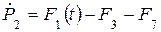Но F₃ – выход по усилию TF, вход в который по усилию идет по связи 4, откуда F₃ = r×F₄. В свою очередь F₄ задано 1-узлом, вход в который идет по связям 5 и 6, т.е. 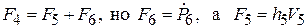. Поток на связи 5 (V₅) определен как выход по потоку 1-узла, вход в который осуществлен по связи 4, т.е. 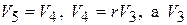– выход 1-узла, вход в который по потоку идет по связи 2, т.е. V₃ = V₂. Поток V₂ – выход эле­мента J₂, вход в который осуществляется по усилию P₂ в соответствии с уравнением элемента 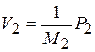. Таким образом,

.

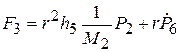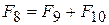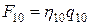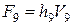Усилие на связи 7 (F₇) – выход из 0-узла, вход в который по усилию дает связь 8, т.е. F₇ = F₈. Но F₈ – выход по усилию 1-узла, вход в который идет по связям 9 и 10: . В свою очередь , а , где 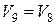. Переменная V₈ – выход 0-узла по скорости, вход в который осуществлен по связям 7 и 11, т.е. 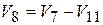. Но V₇ = V₂, а 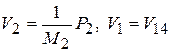, где .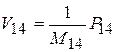

Окончательно уравнение для ( 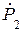) имеет вид

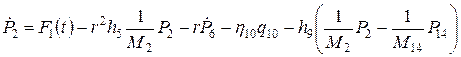; (a)

2. Переменная P₆.

Переменная P₆ – выход элемента J₆, вход в который идет по потоку V₆, откуда 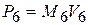. Но V₆ – выход по потоку 1-узла, входом в который является V₄. 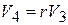, а .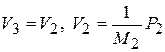

Окончательно:

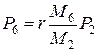; (b)

3. Переменная q₁₀.

Двигаясь по графу в соответствии с причинно-следственными соотношениями, получим

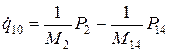; (c)

4. Переменная P₁₄.

Аналогично п.п.1,2,3 имеем:

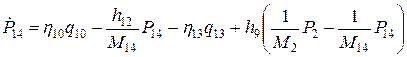; (d)

5. Переменная q₁₃.

Аналогично п.1–4 имеем:

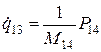. (e)

Таким образом, описание системы, схема которой приведена на рис.2.1 включает пять уравнений (а, в, с, d, е), содержащих пять неизвестных. Причем порядок этой системы равен 4 и определен числом на­капливающих элементов с интегральной причинностью.