Мгновенный центр ускорений

В каждый момент движения плоской фигуры в своей плоскости, если ω и ε не равны нулю одновременно, имеется единственная точка этой фигуры, ускорение которой равно

нулю. Эту точку называют мгновен­ным центрам ускорений. Обозначим ее через Q. Для доказательства этой теоремы предположим, что известны по модулю и направлению ускорение какой-либо точки плоской фигуры, угловая скорость и угловое ускорение этой фигуры. Пусть φ’’< 0 (рис. 56). Мгновенный центр ускорений лежит на линии, проведенной под углом а к ускорению точки, тангенс кото­рого вычисляем по формуле tgα= ε/ω².

При этом угол α надо отложить от ускорения а₀ в направлении дуговой стрелки углового ускорения е, т. е. в рассматриваемом случае по часовой стрелке. Только в точках этой прямой ускорение а₀ и ускорение от вращения a_QO могут иметь противоположные направления и одинаковые значения т.е.

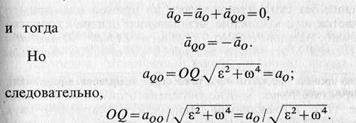
Из приведенного доказательства следует, что мгновенный центр ускорений является единственной точкой плоской фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры. Если мгновенный центр ускорений известен, то, выбрав его за полюс, для ускорения точки А плоской фигуры по формуле (10) получаем (16)

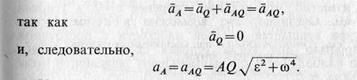
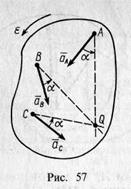
Ускорение а_А направлено под углом α к отрезку AQ, соединяющему точку А с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения е (рис. 57).

Для точки В, аналогично, (17)

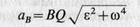
и ускорение а_в также направлено под углом α к отрезку BQ. Из формул (16) и (17) имеем

a_A/a_B = AQ/BQ, (18)

т. е. ускорения точек плоской фигуры при плоском движении пропорциональны рас­стояниям от этих точек до мгновенного центра ускорений.

Итак, суммируя результаты, получаем, что ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью ω и угловым ускорением ε.

Для вычисления скоростей точек плоской фигуры при плоском движении принимают, что плоская фигура вращается вокруг мгновенного центра скоростей, а для вычисления ускорения следует считать, что она вращается вокруг мгновен­ного центра ускорений.

При качении без скольжения колеса по прямой получается, что ускорение мгновенного центра скоростей не равно нулю; следовательно, в общем случае мгновенные центры скоростей и ускорений являются различными точками плоской фигуры.

Рассмотрим способы нахождения мгновенного центра уско­рений,

1. Пусть известно, что угловое ускорение ε = 0, а угловая скорость ω#0. Очевидно, это возможно в случае, когда плоская фигура вращается в своей плоскости с постоянной угловой скоростью или когда угловая скорость достигает относительно наибольшего или наименьшего значения. В этом случае для угла α tg α =ε/ω²

и, следовательно, угол α=0

Мгновенный центр ускорений лежит на прямой линии, по которой направлено ускорение какой-либо точки плоской

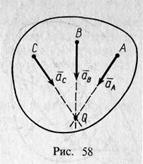фигуры (рис. 58). Так как это справедливо для любой точки фигуры то, следователь­но, мгновенный центр ускорений лежит в точке пересечения прямых линий, по которым направлены ускорения точек плоской фигуры. Ускорения точек плоской фигуры в этом случае направлены к мгно­венному центру ускорений, так как они состоят только из одной относительной нормальной составляющей от вращения вокруг мгновенного центра ускорений.

Если известно ускорение, например точки А центр ускорений можно найти по расстоянию AQ: AQ=a_A//ω²

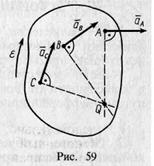
2. Пусть угловая скорость ω=0, а угловое ускорение ε#0. Это возможно при мгновенном поступательном движении. Тогда tg α =ε/ω²=∞

и, следовательно, угол α— прямой. Его надо откладывать от ускорения точки в направлении дуговой стрелки углового ускорения. Мгновенный центр ускорений лежит на пересечении перпендикуляров к ускорениям точек плоской фигуры, про­веденных из этих точек (рис. 59).

Мгновенный центр ускорений лежит на пересечении прямых линий, проведенных к ускорениям точек фигуры под одним и тем же углом α, причем угол ос нужно откладывать от ускорений точек в на­правлении дуговой стрелки углового ускорения независимо от направления угловой скорости плоской фигуры (см. рис. 57)