Функции и способы их задания.

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

И ПЛАН ПРОВЕДЕНИЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ

Направление подготовки бакалавра 20.03.01 «Техносферная безопасность»

Профиль «Пожарная безопасность»

по учебной дисциплине «Высшая математика»

Тема № 1. Введение в математический анализ.

Занятие 1.2. Функции и способы их задания.

Учебные группы: 121 – 124.

Обсуждены на заседании

методической секции «Высшая математика»

Протокол № 12 от

«31» июля 2014 года

I. Цели и задачи занятия

1. Выработать навыки построения графиков основных элементарных функций.

2. Показать обучающимся важность данной темы в курсе изучаемой дисциплины.

3. Воспитывать у обучающихся настойчивость в достижении поставленной цели.

II. Расчет учебного времени

Содержание и порядок проведения занятия	Время, мин
ВВОДНАЯ ЧАСТЬ
ОСНОВНАЯ ЧАСТЬ Учебные вопросы:
1. Функции и способы их задания.
2. Исследование графиков функций.
ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ

III. Учебно-материальное обеспечение

Классная доска, раздаточный материал.

IV. Методические материалы

К проведению практического занятия

Во вводной части занятия (5 мин.) после объявления темы и целей практического занятия целесообразно изложить последовательность обсуждения учебных вопросов.

Первый учебный вопрос (10 мин).

Функции и способы их задания.

Вопросы, задаваемые обучающимся:

1. Определение функции

2. Способы задания функции

3. Основные характеристики функций.

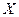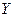Определение: Пусть даны два множества и (непустых). Соответствие 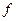, которое каждому элементу 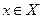сопоставляет один и только один элемент 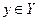называется функцией и записывается 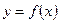или 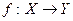(говорят еще, что функция 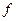отображает множество 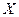на множество ).

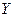Наиболее часто встречаются следующие способы задания функции: аналитический, графический, табличный.

Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.

Аналитический способ является наиболее совершенным, т.к. к нему приложены методы математического анализа, позволяющие полностью исследовать функцию.

Графический способ: задается график функции.

Графиком функции 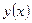называется множество всех точек 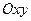, абсциссами которых являются аргументы ( 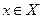), а ординатами – соответствующие им значения функции.

Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известны таблицы значений тригонометрических функций, логарифмические таблицы. На практике часто приходится пользоваться таблицами значений функции, полученных опытным путем или в результате наблюдений.

1) Функция 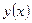называется четной, если для любого 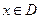выполняется условие 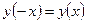( 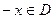). График четной функции симметричен относительно оси .

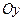Функция 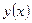называется нечетной, если для любого 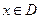выполняется условие 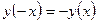. График нечетной функции симметричен относительно начала координат.

2) Функция 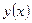называется возрастающей, если для любых 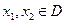таких, что 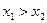выполняется неравенство 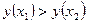. Функция 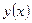называется убывающей, если для любых 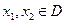таких, что 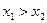выполняется неравенство 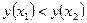. Эти функции называются монотонными. Интервалы, в которых функция монотонная называются интервалами монотонности.

3) Функция 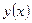называется ограниченной, если существует такое число 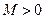, что для всех 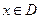выполняется неравенство 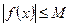. Следовательно, график функции лежит между прямым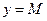и и .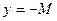

4) Функция 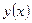называется периодической, если существует такое число 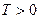, что для всех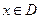 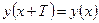(если 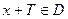). При этом число 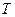называется периодом функции.