Порядок выполнения работы на компьютере и обработка результатов измерений
1. Выбрать из списка на экране название работы ЭМК-7, подвести к нему с помощью мыши курсор и дважды щелкнуть левой кнопкой мыши. После раскрытия пакета установить курсор на Lab и дважды щелкнуть мышью. Появляется титульный лист с названием, целью и поставленной задачей данной лабораторной работы и ниже - содержание данной работы, включающее Теорию, Работу, Тесты и Выход. Выход используется после завершения работы, но позволяет закрыть программу в любой нужный момент.
2. Щелкнув мышью по Теории, ознакомьтесь с теоретическим введением и методикой эксперимента, рабочими формулами и описанием экспериментальной установки, а также порядком проведения работы. Вернитесь к Основному меню, нажав на соответствующую надпись.
3. Тесты (24 для данной работы) применяются по указанию преподавателя либо для допуска к работе, либо для ее защиты.
4. Дважды щелкнув по Работе, вы перейдете к следующему кадру с выбором заданий. В задании № 1 (Упражнение 1) необходимо собрать измерительную схему. Для этого можно воспользоваться справкой, нажав мышью на Помощь.
5. Собрав схему, установите курсор на Далее и нажмите левой кнопкой мыши, появится экспериментальная цепь. Здесь подразумевается, что движок 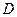 потенциометра установлен в верхнее крайнее положение и источник
потенциометра установлен в верхнее крайнее положение и источник 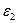 не подключен. В магазине сопротивлений установите с помощью левой кнопки мыши значение
не подключен. В магазине сопротивлений установите с помощью левой кнопки мыши значение 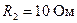 и запишите показания амперметра
и запишите показания амперметра 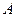 и вольтметра
и вольтметра 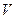 . Далее снимите полную зависимость
. Далее снимите полную зависимость 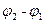 от
от 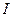 , изменяя значения внешнего сопротивления
, изменяя значения внешнего сопротивления 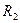 до 80 Ом через 10 Ом с помощью мыши или, что удобнее, с помощью стрелки «вправо» на клавиатуре.
до 80 Ом через 10 Ом с помощью мыши или, что удобнее, с помощью стрелки «вправо» на клавиатуре.
6. Все полученные данные заносятся в таблицу 1.
Т а б л и ц а 1
| № | Показания амперметра 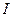 , А , А | Показания вольтметра 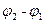 , В , В | |
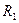 |
7. Построить график зависимости функции 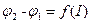 (рисунок 3.2). При помощи графика определить значение
(рисунок 3.2). При помощи графика определить значение 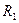 (формула 3.10).
(формула 3.10).
8. В упражнении 2 задания 1 замените 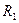 на
на 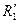 , большее, чем
, большее, чем 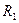 , щелкнув левой кнопки мыши по соответствующей надписи в левом нижнем углу кадра. Тогда появится рабочая цепь с подключенным с помощью ключа
, щелкнув левой кнопки мыши по соответствующей надписи в левом нижнем углу кадра. Тогда появится рабочая цепь с подключенным с помощью ключа 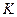 источником
источником 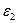 и движком
и движком 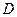 в произвольном положении на потенциометре. Снимите зависимость
в произвольном положении на потенциометре. Снимите зависимость 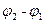 от
от 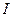 аналогичным образом, изменяя сопротивление магазина
аналогичным образом, изменяя сопротивление магазина 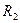 от 180 до 20 Ом с помощью стрелки «вправо» на клавиатуре. (Обратите внимание на то, что последние показания вольтметра
от 180 до 20 Ом с помощью стрелки «вправо» на клавиатуре. (Обратите внимание на то, что последние показания вольтметра 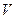 могут иметь отрицательные значения).
могут иметь отрицательные значения).
9. Все полученные данные заносятся в таблицу 2. Повторить пункт 7, используя данные таблицы 2.
Т а б л и ц а 2
| № | Показания амперметра 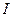 , А , А | Показания вольтметра 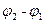 , В , В | |
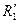 |
10. В Выборе задания перейдите к заданию 2.
Задание 2.
1. Сначала производится сборка схемы электрической цепи. После нажатия на Далее с помощью мыши появляется рабочая цепь для измерений.
2. В упражнении 1 измеряются значения силы тока и напряжения при ЭДС ( 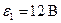 ) на генераторе напряжения ГН-2 с помощью магазина сопротивлений (
) на генераторе напряжения ГН-2 с помощью магазина сопротивлений ( 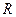 изменяется от 100 до 900 Ом через каждые 100 Ом). Данные заносятся в таблицу 3.
изменяется от 100 до 900 Ом через каждые 100 Ом). Данные заносятся в таблицу 3.
Т а б л и ц а 3
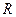 | 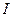 , A , A | 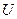 , B , B | 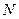 , Вт , Вт |
3. Значения мощности вычисляются по формуле 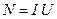 и строятся графики зависимости полезной мощности от сопротивления нагрузки.
и строятся графики зависимости полезной мощности от сопротивления нагрузки.
4. В упражнении 2 измеряются значения силы тока и напряжения при изменении ЭДС ( 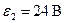 ) на генераторе напряжения ГН-2 с помощью магазина сопротивлений (R' изменяется от 100 до 900 Ом через каждые 100 Ом). Данные заносятся в таблицу 4.
) на генераторе напряжения ГН-2 с помощью магазина сопротивлений (R' изменяется от 100 до 900 Ом через каждые 100 Ом). Данные заносятся в таблицу 4.
Т а б л и ц а 4
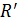 | 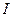 , A , A | 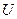 , B , B | 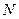 , Вт , Вт |
5. Повторить пункт 3, используя данные таблицы 4.
6. Из графиков определяются значения сопротивлений при максимальной мощности и путем вычитывания известного дополнительного сопротивления 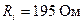 определяется внутреннее сопротивление источника.
определяется внутреннее сопротивление источника.
7. Проанализировать результаты и сформулировать выводы.
Контрольные вопросы
1. Что называется силой тока? плотностью тока? Каковы их единицы? (Дать определения.)
2. Назовите условия возникновения и существования электрического тока.
3. Что такое сторонние силы? Какова их природа?
4. В чем заключается физический смысл электродвижущей силы, действующей в цепи? напряжения? разности потенциалов?
5. Почему напряжение является обобщенным понятием разности потенциалов?
6. Выведите законы Ома в дифференциальной форме.
