Понятие о двойственных задачах линейного программирования
Задача №4.2.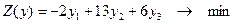 
; 
, 
.
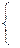
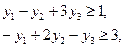
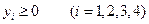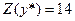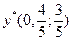Задача №4.3.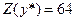 
; 
.
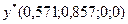Задача №4.4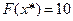 
, 
.
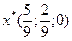Транспортная задача
Задача № 5.3.Транспортные расходы по доставке груза всем трем пуктам потребления приоптимальном планировании
,
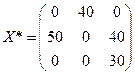будут равны 320 д.е. При этом от второго поставщика груз будет вывезен не полностью, там останется 20 ед. груза.
Задача № 5.4.Оптимальное решение:
,
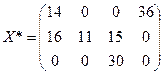при котором транспортные расходы по обеспечению продуктом всех четырех пуктов потребления будут наименьшими. При этом из второго пункта производства товар будет вывезен не полностью, там останется остаток продукта 28 единиц.
Элементы теории игр
Задача № 6.9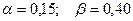 
.
Задача № 6.10 Игра имеет решение в чистых стратегиях. Оптимальные стратегии: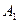 
- для игрока 
; 
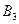- для игрока 
. Чистая цена игры 
.
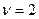Задача № 6.11 Игра имеет решение в чистых стратегиях. Оптимальные стратегии: 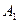- для игрока ; 
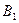- для игрока . Чистая цена игры 
.
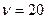Задача № 6.12 Игра не имеет решения в чистых стратегиях: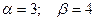 
.
Чистая цена игры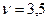 
. Оптимальные стратегии: 
; 
.
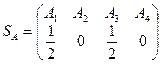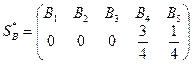Задача № 6.13 Игра не имеет решения в чистых стратегиях: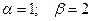 
.
Чистая цена игры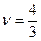 
. Оптимальные стратегии: 
; 
.
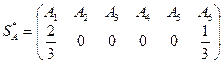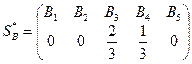Варианты типовых расчетов
ВАРИАНТ №1
№1. Используя графический метод и теоремы двойственности минимизировать целевую функцию Z(Y)=4y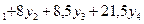 
при условии выполнения ограничений:
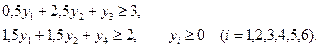
№2. Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 4770 кг, сырьем второго вида в количестве 5610 кг, сырьем третьего вида в количестве 4820 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -9 кг, сырья второго вида - 5 кг, сырья третьего вида - 7 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 5 кг, сырья второго вида - 11 кг, сырья третьего вида - 8 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 16 руб., 23 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет сij рублей. Эти стоимости также указаны в распределительной таблице.
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | Базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |  3300 |
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей.
№4. Игра задана платежной матрицей А:
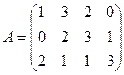
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №2
№1. Решить задачу графически, используя теоремы двойственности:
Z(Y)=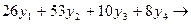 
min
При условии выполнения ограничений:
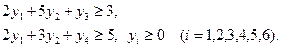
№2. . Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 5700 кг, сырьем второго вида в количестве 5190 кг, сырьем третьего вида в количестве 6450 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -2 кг, сырья второго вида - 3 кг, сырья третьего вида - 5 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 5 кг, сырья второго вида - 4 кг, сырья третьего вида - 3 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 14 руб., 30 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей.
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4.Игра задана платежной матрицей А:
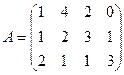
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №3
№1.Решить задачу графически, используя теоремы двойственности:
Z(Y)=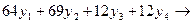 
min
При условии выполнения ограничений:
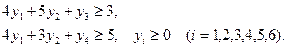
№2. Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 4950 кг, сырьем второго вида в количестве 7260 кг, сырьем третьего вида в количестве 3420 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -5 кг, сырья второго вида - 6 кг, сырья третьего вида - 1 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 4 кг, сырья второго вида - 7 кг, сырья третьего вида - 4 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 10 руб., 19 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
 Потребн. предпр. |
№4. Игра задана платежной матрицей А:
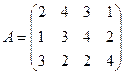
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
Вариант №4
№1.Решите задачу графически, используя теоремы двойственности:
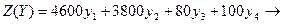min
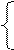при условии, выполнения ограничений:
№2. . Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 5580 кг, сырьем второго вида в количестве 6000 кг, сырьем третьего вида в количестве 5400 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -4 кг, сырья второго вида - 3 кг, сырья третьего вида - 6 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 7 кг, сырья второго вида – 8 кг, сырья третьего вида - 4 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 18 руб., 23 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | Базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4.Игра задана платежной матрицей А:
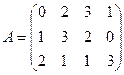
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №5
№1.Решить задачу графически, используя теоремы двойственности:
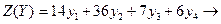min
при условии, выполнения ограничений:
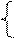
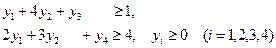
№2.. Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 5040 кг, сырьем второго вида в количестве 4410 кг, сырьем третьего вида в количестве 3540 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -7 кг, сырья второго вида - 3 кг, сырья третьего вида - 4 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 6 кг, сырья второго вида - 7 кг, сырья третьего вида - 5 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 13 руб., 22 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4. Игра задана платежной матрицей А:
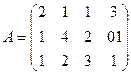
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №6
№1.Решите задачу графически, используя теоремы двойственности:
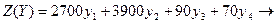min
при условии, выполнения ограничений:
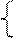
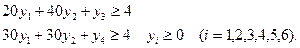
№2.Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 3780 кг, сырьем второго вида в количестве 8460 кг, сырьем третьего вида в количестве 4800 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -3 кг, сырья второго вида - 5 кг, сырья третьего вида - 1 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 2 кг, сырья второго вида - 6 кг, сырья третьего вида - 4 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 20 руб., 16 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей.
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4.Игра задана платежной матрицей А:
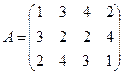
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №7
№1.Решите задачу графически, используя теоремы двойственности:
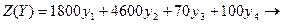min
при условии, выполнения ограничений:
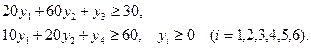
№2. . Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 6960 кг, сырьем второго вида в количестве 8820 кг, сырьем третьего вида в количестве 5760 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -3 кг, сырья второго вида - 2 кг, сырья третьего вида - 4 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 5 кг, сырья второго вида - 7 кг, сырья третьего вида - 3 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 12 руб., 26 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей.
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4.Игра задана платежной матрицей А:
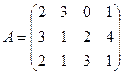
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №8
№1.Решите задачу графически, используя теоремы двойственности:
Z(Y)=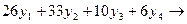 
min
При условии выполнения ограничений:
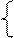
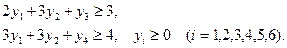
№2. . Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 6600 кг, сырьем второго вида в количестве 7920 кг, сырьем третьего вида в количестве 6720 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -6 кг, сырья второго вида - 2 кг, сырья третьего вида - 8 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 7 кг, сырья второго вида - 11 кг, сырья третьего вида - 5 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 13 руб., 27 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4.Игра задана платежной матрицей А:
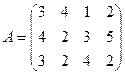
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №9
№1.Решите задачу графически, используя теоремы двойственности:
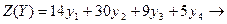min
при условии, выполнения ограничений:
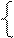
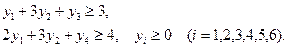
№2. Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 7710 кг, сырьем второго вида в количестве 8910 кг, сырьем третьего вида в количестве 7800 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -5 кг, сырья второго вида - 9 кг, сырья третьего вида - 3 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 9 кг, сырья второго вида - 7 кг, сырья третьего вида – 10 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 10руб., 22 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей.
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4.Игра задана платежной матрицей А:
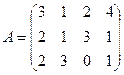
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ВАРИАНТ №10
№1.Решите задачу графически, используя теоремы двойственности:
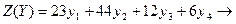min
при условии, выполнения ограничений:
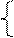
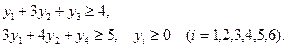
№2. Для производства двух видов изделий используется три вида сырья. Запасы сырья ограничены, предприятие обеспечено сырьем первого вида в количестве 6390 кг, сырьем второго вида в количестве 6750 кг, сырьем третьего вида в количестве 4440 кг.
На производство одного изделия первого вида необходимо затратить сырья первого вида -5 кг, сырья второго вида - 4 кг, сырья третьего вида - 4 кг. На производство одного изделия второго вида необходимо затратить сырья первого вида - 8 кг, сырья второго вида - 9 кг, сырья третьего вида - 5 кг.
Прибыль от реализации одного изделий первого и второго видов составляет 17 руб., 26 руб. соответственно.
Составить план производства изделий так, чтобы предприятие получило наибольшую прибыль от их реализации. Задачу решить симплексным методом.
№3.На трех базах Б1, Б2, Б3 находится однородный груз. Этот груз необходимо перевезти на пять предприятий П1, П2, П3, П4, П5. Запасы груза на базах, потребности предприятий в этом грузе указаны в распределительной таблице. Стоимость перевозки одной тонны груза с базы Бi на предприятие Пj составляет Сij рублей. Эти стоимости также указаны в распределительной таблице.
Необходимо спланировать перевозки так, чтобы их общая стоимость была наименьшей.
| Предприятия | Запасы на | |||||
| Базы | П1 | П2 | П3 | П4 | П5 | базах |
| Б1 | ||||||
| Б2 | ||||||
| Б3 | ||||||
| Потребн. предпр. |
№4.Игра задана платежной матрицей А:
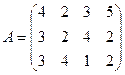
Определить нижнюю и верхнюю цены игры. Свести матричную игру к задаче ЛП. Найти решение игры, используя Excel («Поиск решений»).
ЛИТЕРАТУРА
1. Высшая математика для экономистов. Учебное пособие для вузов / Под ред. проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
2. Данко П.Е., Попова А.Г. «Высшая математика в упражнениях и задачах». Ч. 1, 2. М.: «Высшая школа», 1986.
3. Малыхин В.М. «Математика в экономике». М.: «ИНФРА-М». 2001 г.
4. Красс М.С. «Математика для экономических специальностей». М.: «ИНФРА-М». 1999г.
5. Красс М.С., Чупрынов Б.П. «Основы математики и ее приложения в экономическом образовании. М.: «Дело». 2000г.
6. Исследование операций в экономике. Под ред. проф. Н.Ш. Кремера. М.: «Банки и биржи», 1997.
7. Колемаев В.А. Математическая экономика. М.: ЮНИТИ, 1998.
8. Шишкин Е.В., Чхартишвили А.Г. «Математические методы и модели в управлении». М.:Дело.2002
9. Бережная Е.В., Бережной В.И. «Математические методы моделирования экономических систем». М.: Финансы и статистика. 2002.
10. Чупрынов Б.П. «Методы оптимизации в экономике». Самара: СГЭА.2000.
11. Экономико-математические методы и прикладные модели. Под ред. В.В. Федосеева. М.: ЮНИТИ. 2002.
12. Просветов Г.И. Математические модели в экономике. Учебно-методическое пособие. М.:РДЛ. 2005.
13. Просветов Г.И. Математические методы в экономике. Учебно-методическое пособие. М.:РДЛ. 2005.
14. Экономико-математические методы и прикладные модели. Под ред. В.В. Федосеева. М.: ЮНИТИ. 2002.
15. Математические методы в экономике. О.О. Замков,Ю.А., Черемных, А.В. Толстопятенко. М.: «Дело и сервис». 1999.
16. Справочник по математике для экономистов. Учебное пособие под ред. проф. В.И.Ермакова. М.:ИНФРА-М. 2007.
17. Шапкин А.С., Мазаева Н.П. Математические методы и модели исследования операций. Учебник. М.:Издательско-торговая корпорация «Дашков и К». 2006.