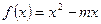По закону Джоуля-Ленца

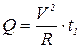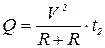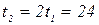, , (мин.)

6. Два тела массами 1 и 3 кг соединены нитью, перекинутой через блок. Определить реакцию блока при движении тел. Трением в блоке и его массой пренебречь.

Дано: m1 = 1 кг m2 = 3 кг_ Найти R

Решение: 2 закон Ньютона

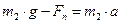
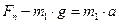
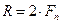
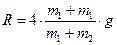
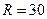
Ответ: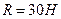

7. Груз массой 50 кг поднят при помощи каната вертикально вверх в течении двух секунд на высоту 10 м. Определить силу натяжения каната, если движение было равноускоренным. Начальная скорость груза равна нулю.

Дано: m = 50 кг t = 2 с H = 10 м__ Найти Fн

Решение: 2 закон Ньютона

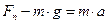
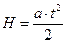
Решая систему уравнений, получим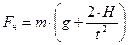

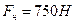
Ответ: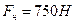

Дано m1 = 2 кг m2 = 6 кг__ Найти Fн

8. Через блок, массой которого можно пренебречь, перекинута нить, к концам которой подвешены две гири массами 2 и 6 кг. Найти натяжение нити при движении гирь.

Решение:

2 закон Ньютона

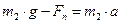
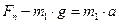
Решая систему уравнений, получим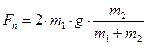

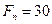
Ответ: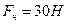

9. Один конец пружинки жесткостью 100 Н/м привязан к потолку лифта, а к другому концу привязана гирька массой 100 г. Определить ускорение лифта, если пружинка растянулась на 1,2 см.

Дано k = 100Н/м m = 100 г х = 1,2 см__ Найти а

Решение:

2 закон Ньютона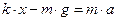

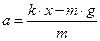
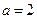
Ответ: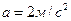

6. Варианты первого тура вступительных испытаний:

Класс

I вариант

(8 класс 1997 г.)

1. Может ли существовать прямоугольный параллелепипед, длины рёбер которого натуральные числа, а площадь поверхности простое число?

2. На сколько процентов уменьшится площадь квадрата, если сторону уменьшить на 10%?

3. Скорость катера в стоячей воде 20 км/ч, скорость течения реки 2 км/ч. Катер проплыл 10 км по течению и 10 км против течения. Определить среднюю скорость катера.

4. На доске нарисован треугольник. Как построить центр описанной окружности?

5. Найти двузначное число, которое равно сумме числа его десятков и квадрата числа единиц.

I вариант

(8 класс 1998 г.)

1. Решить неравенство: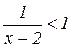

2. Увеличится или уменьшится правильная положительная дробь 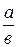, если к числителю прибавить одно и тоже положительное число d?

3. Можно ли любой остроугольный треугольник, не имеющий равных сторон, рассечь прямой, проходящей через вершину, на 2 подобных треугольника?

4. Дан треугольник АВС, Н – точка пересечения его высот. ВН=АС. Найти угол АВС.

II вариант

(8 класс 1998 г.)

1. Решить неравенство: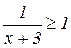

2. Построить график функции: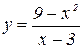

3. Катеты прямоугольного треугольника равны 16 и 12 м. Найти медиану, проведённую к гипотенузе.

4. Можно ли любой остроугольный треугольник, не имеющий равных сторон, рассечь прямой, проходящей через вершину на 2 подобных треугольника?

I вариант

(8 класс 1999 г.)

1. Дана функция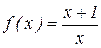

1.1 . Решить неравенство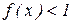

1.2 . Решить уравнение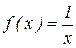

1.3 . Построить график функции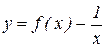

2. Моторная лодка прошла от города М до города К по течению реки за 8 часов, а от К до М за 12 часов. За сколько часов проплывает плот от города М до города К?

3. Катеты прямоугольного треугольника равны а и 2а. Найти длины отрезков, на которые основание высоты, проведённой из вершины прямого угла, делит гипотенузу.

4. Докажите, что если биссектрисы углов АВС и СBD перпендикулярны, то точки А, В и D лежат на одной прямой.

II вариант

(8 класс 1999 г.)

1. Дана функция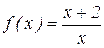

1.1 . Решить неравенство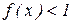

1.2 . Решить уравнение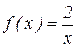

1.3 . Построить график функции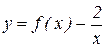

2. Два каменщика сложили вместе стену за 20 дней. За сколько дней выполнил бы работу каждый из них отдельно, если известно, что первый должен работать на 9 дней больше второго?

3. Катеты прямоугольного треугольника равны а и 2а. Найти длину высоты, опущенной из вершины прямого угла на гипотенузу.

4. Докажите, что биссектрисы вертикальных углов лежат на одной прямой.

I вариант

(8 класс, 2000 г.)

1. Упростить: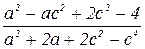

2. При каких значениях с уравнение 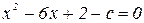имеет 2 корня разных знаков?

3. У мальчика столько сестер, сколько и братьев, а у его сестры вдвое меньше сестер, чем братьев. Сколько братьев и сколько сестер в семье?

4. В остроугольном треугольнике АВС проведены высоты ВВ₁ и СС₁. Докажите, что .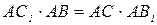

5. Построить график функции: .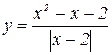

II вариант

(8 класс, 2000 г.)

1. Упростить: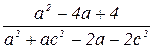

2. При каких значениях а уравнение 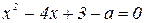имеет 2 корня разных знаков?

3. Отец старше дочери в 4 раза. Пять лет назад он был старше её в 9 раз. Сколько лет сейчас отцу и дочери?

4. В остроугольном треугольнике АВС проведены высоты АА₁ и ВВ₁. Докажите, что .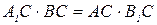

5. Построить график функции: .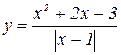

I вариант

(8 класс, 2001г.)

1. Сократить дробь: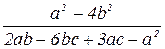

2. Дано квадратное уравнение х²-4х+1=0. Составьте такое квадратное уравнение, чтобы его корни отличались от корней данного уравнения только знаками.

3. Для каких положительных m верно неравенство ?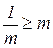

4. В равнобедренной трапеции АВСD основания AD = 9 см, ВС = 7 см, а диагональ АС = 10 см. Определить периметр данной трапеции.

5. Катет равнобедренного прямоугольного треугольника равен 6. Найти медиану, проведённую из вершины острого угла.

6. Шофёр грузовой машины рассчитал, что, двигаясь со скоростью 40 км/ч, он прибудет в город М в назначенный срок. Однако, пройдя 2/5 всего пути, он сделал вынужденную остановку на 20 мин. Чтобы прибыть в город М в срок, остальной путь он ехал со скоростью 45 км/ч. Найдите расстояние до города М.

7. Ромашка при сушке теряет 84% своей массы. Сколько ромашки надо собрать, чтобы сдать в аптеку 16 кг высушенных цветов?

II вариант

(8 класс, 2001 г.)

1. Сократить дробь: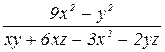

2. Дано квадратное уравнение х²-3х+2=0. Составьте такое квадратное уравнение, чтобы его корни отличались от корней данного уравнения только знаками.

3. Для каких отрицательных nверно неравенство ?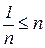

4. В равнобедренной трапеции основания равны 2 и 6. Диагональ равна 5. Найти периметр.

5. Определить острые углы прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 1:2.

6. Турист, идущий из деревни на станцию, пройдя за первый час 3 км, рассчитал, что он опоздает к поезду на 40 мин, если будет двигаться с той же скоростью. Поэтому остальной путь он проходит со скоростью 4 км/ч и прибывает на станцию за 45 мин до отхода поезда. Каково расстояние от деревни до станции?

7.На участке прямоугольной формы, длина которого на 10 м больше его ширины, имеется газон площадью 1600 м². Найти длину и ширину участка, если площадь газона составляет 80% площади участка.

II вариант

(8 класс, 2002 г.)

1. Расстояние между двумя городами 80 км. Теплоход тратит на этот путь в оба конца 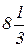часа. Найти скорость теплохода в стоячей воде, если скорость течения 4 км/час.

2. Определить острые углы прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 2:3.

3. В равнобедренном треугольнике длина боковой стороны равна 5, а длина высоты, опущенной на основание, равна 4. Найти длину основания.

4. В прямоугольнике со сторонами 1м×2м от каждой стороны отрезаются полоски шириной 20 см. Сколько процентов составляет площадь полученного прямоугольника от первоначальной?

5. Один из корней уравнения 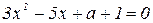равен 1. Найдите другой корень.

I вариант

(8 класс, 2003г.)

1. При каком а решением неравенства 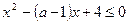является единственное значение x.

2. Построить график функции: .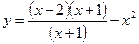

3. На покупку велосипедов школа выделила 6000 руб. Так как цена велосипеда снизилась на 250 руб., то на эту сумму куплено на 4 велосипеда больше, чем предполагалось. Сколько велосипедов было куплено?

4. На сколько надо увеличить число 252, чтобы 39 % от него были бы равны 234.

5. Катет прямоугольного треугольника больше другого катета на 10 и меньше гипотенузы на 10. Найдите периметр треугольника.

6. Найдите боковую сторону равнобедренного треугольника, если его основание равно 4см, а медиана боковой стороны 5 см.

II вариант

(8 класс, 2003г.)

1. При каком а решением неравенства 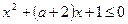является единственное значение x.

2. Построить график функции: .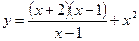

3. Отец старше дочери в 4 раза. 5 лет назад он был старше её в 9 раз. Сколько сейчас лет отцу и сколько дочери?

4. Цену изделия снизили на 10 %. Затем новую цену снизили на 20 %. После этого стоимость изделия оказалась равной 72 %. Найти первоначальную стоимость изделия.

5. Высота прямоугольного треугольника, проведённая из вершины прямого угла к гипотенузе, равна 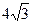. Один из катетов равен. 8. Найти периметр и площадь треугольника.

6. Найдите основание равнобедренного треугольника, если его боковая сторона равна 6см, а медиана боковой стороны 5 см.

I вариант

(8 класс, 2005г.)

1. Решите уравнение: .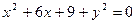

2. При каких целых а выражения 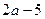и 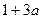имеют разные знаки.

3. Упростить выражение и построить график функции . .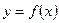

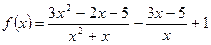4. На сколько процентов увеличится площадь квадрата, если периметр его увеличить на 10%?

5. Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

6. Катет прямоугольного треугольника больше другого катета на 10 и меньше гипотенузы на 10. Найдите периметр треугольника.

II вариант

(8 класс, 2005г.)

1. Решите уравнение: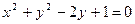

2. При каких целых а выражения 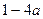и 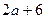имеют разные знаки.

3. Упростить выражение и построить график функции . .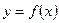

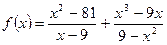4. На сколько процентов увеличится площадь прямоугольника, если длину прямоугольника увеличить на 20%, а ширину – на 10%?

5. Стороны параллелограмма равны 12 см и 4 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

6. Высота прямоугольного треугольника, проведённая из вершины прямого угла к гипотенузе, равна 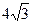. Один из катетов равен. 8. Найти периметр треугольника.

2006г. (I тур), I вариант

1. Молоко даёт 25% сливок, сливки дают 20% масла. Сколько масла получается из 240 кг молока?

2. Найдите сумму корней уравнения .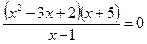

3. При каких целых а выражение а+1 и 3-а имеют одинаковые знаки?

4. Построить график функции .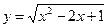

5. Доказать, что значение выражения 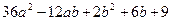неотрицательно при любых значениях а и b. Найти а и b, при которых это выражение принимает наименьшее значение.

6. Меньшее основание равнобедренной трапеции равно 10, боковая сторона 18, а диагональ 22. Найдите большее основание трапеции.

2006г. (I тур), II вариант

1. Лоси составляют 30% от общего числа косуль и лосей, живущих в заповеднике. Сколько косуль живёт в заповеднике, если число лосей на 144 меньше числа косуль?

2. Найдите сумму корней уравнения .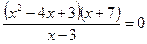

3. При каких целых а выражение а-3 и 4+а имеют разные знаки?

4. Построить график функции .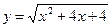

5. Доказать, что значение выражения 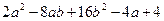неотрицательно при любых значениях а и b. Найти а и b, при которых это выражение принимает наименьшее значение.

6. Основания равнобедренной трапеции равны 3 и 8, а угол при основании 60°. Найдите диагональ.

2007г. (I тур), I вариант

1. В коробке лежат несколько одинаковых пачек печенья. Если из коробки вынуть 7 пачек, то в ней останется ¼ всего количества пачек, которое в ней может поместиться. Если же добавить ¾ от имеющегося количества пачек, то одна пачка не поместится. Сколько пачек печенья лежит в коробке?

2. При каких значениях m значение выражения 10m+1 не меньше значений выражения 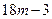, если ?

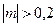3. Известно, что 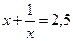. Найдите .

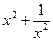4. Докажите неравенство 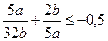, если а и b – числа разных знаков.

5. Основания равнобедренной трапеции равны 3 и 8, а угол при основании 60º. Найдите диагональ.

6. Найти площадь треугольника, ограниченного графиками функций 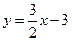, 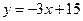и осью Ох.

2007г. (I тур), II вариант

1. В ведре было несколько литров воды. Если отлить половину всей воды, то там останется на 7 л воды меньше, чем помещается в ведро. Если же добавить 2л, то количество воды составит 2/3 вместимости ведра. Сколько литров воды было в ведре?

2. При каких значениях y значение выражения 3-2y не меньше значения выражения 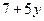, если ?

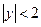3. Известно, что 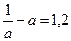. Найдите .

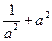4. Докажите неравенство 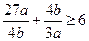, если а и b – числа одного знака.

5. Боковая сторона равнобедренной трапеции равна 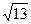, основания равны 3 и 4. Найдите диагональ трапеции.

6. Найти площадь треугольника, ограниченного графиками функций 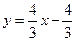, 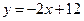и осью Ох.

2008г. (I тур), I вариант

1. Упростить выражение: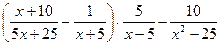

2. Постройте график функции: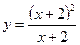

3. При каком х выражение 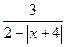не имеет смысла.

4. Найти множество целых значений а при которых произведение 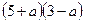- положительно.

5. Из 220 школьников 163 играют в баскетбол, 175 – в футбол, 24 не играют в эти игры. Сколько человек одновременно играют в баскетбол и футбол?

6. В январе завод выполнил 105 % месячного плана выпуска продукции, а в феврале дал продукции на 4% больше, чем в январе. На сколько процентов завод перевыполнил двухмесячный план выпуска продукции?

7. Чему равен острый угол между биссектрисами острых углов прямоугольного треугольника?

2008г. (I тур), II вариант

1. Упростить выражение: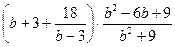

2. Постройте график функции: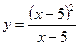

3. При каком х выражение 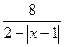не имеет смысла.

4. Найти множество целых значений а при которых произведение 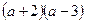- отрицательно.

5. Среди 35 туристов одним английским языком владеют 11 человек, одним французским – 10 человек. 9 человек не владеют ни английским, ни французским. Сколько человек владеют и английским, и французским языками.

6. На сколько процентов увеличится площадь квадрата, если сторону его увеличить на 20%.

7. Боковая сторона равнобедренной трапеции равна 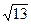, основания равны 3 и 4. Найдите диагональ трапеции.

2009г. (I тур), I вариант

1. При каких значениях х верно двойное неравенство: .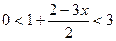

2. Графики линейных функци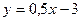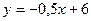й , и 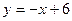, попарно пересекаясь, образуют треугольник. Вычислите координаты его вершин.

3. Машина выехала со скоростью 50км/ч. Через полчаса вслед за ней выехала другая машина, которая догнала её через 2,5 часа. Сколько процентов скорость второй машины составляет от скорости первой?

4. Сократить дробь: .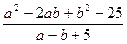

5. При каких m верно равенство: .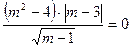

6. АВСD – прямоугольник, в котором АВ=1, ВС=2. На сторонах ВС и DA взяты точки М и N так, что ВМDN – ромб. Найдите сторону ромба.

2009г. (I тур), II вариант

1. При каких значениях х верно двойное неравенство: .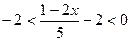

2. Графики линейных функци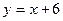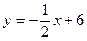й , и 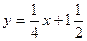, попарно пересекаясь, образуют треугольник. Вычислите координаты его вершин.

3. Турист на лодке проплыл против течения 10 км и по течению 18 км, затратив на весь путь 4 часа. Скорость течения реки равна 2 км/ч. Сколько процентов от скорости течения реки составляет скорость лодки в стоячей воде?

4. Сократить дробь: .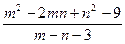

5. При каких m верно равенство: .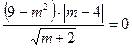

6. В треугольнике АВС проведена биссектриса ВВ₁. Найти углы этого треугольника, если известно, что АВ= ВВ₁= В₁С.

2009г. (I тур), III вариант

1. Найдите решения неравенства 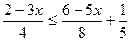принадлежащие промежутку .

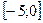2. Графики линейных функци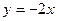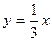й , и 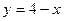, попарно пересекаясь, образуют треугольник. Вычислите координаты его вершин.

3. Пароход прошёл по течению реки 96 км и столько же против течения, затратив на весь путь 10 часов. Скорость течения реки равна 4 км/ч. Сколько процентов скорость течения реки составляет от скорости парохода в стоячей воде?

4. Сократить дробь: .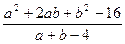

5. При каких а верно равенство: .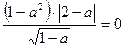

6. В треугольнике АВС известны стороны АС=2, АВ=3, ВС=4. Пусть BD – высота этого треугольника (D – на прямой АС). Найти длину отрезка СD.

2009г. (I тур), IV вариант

1. Найдите решения неравенства 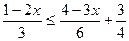принадлежащие промежутку .

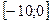2. Графики линейных функци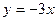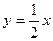й , и 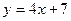, попарно пересекаясь, образуют треугольник. Вычислите координаты его вершин.

3. Из пункта А вышел турист. Через 2 часа вслед за ним выехал велосипедист, скорость которого была на 6 км/ч больше скорости туриста. За 2 часа велосипедист обогнал туриста на 4 км. Сколько процентов скорость туриста составляет от скорости велосипедиста?

4. Сократить дробь: .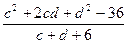

5. При каких а верно равенство: .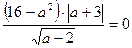

6. Одна сторона треугольника равна 2, прилежащие углы равны 30º и 45º. Найти две оставшиеся стороны этого треугольника.

2010г. (I тур), I вариант

1. На трёх полках лежит всего 66 книг, причём на нижней втрое больше, а на средней вдвое больше, чем на верхней. Сколько книг на каждой полке?

2. Решите уравнение .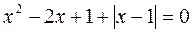

3. При каких m выражения m-3 и m+4 имеют разные знаки?

4. Сократите дробь: .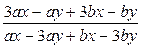

5. В треугольнике АВС известны стороны АС=2, АВ=3, ВС=4. Пусть ВD – высота этого треугольника (D – на прямой АС). Найти длину отрезка СD.

6. Построить график функции .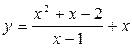

2010г. (I тур), II вариант

1. Часы, цепочка и брелок стоят вместе 7200 руб. Брелок дороже цепочки в два раза, а часы дороже брелка в три раза. Сколько стоят часы, цепочка и брелок в отдельности.

2. Решите уравнение .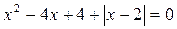

3. При каких m выражения m+1 и m-4 имеют разные знаки?

4. Сократите дробь: .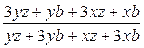

5. Один катет прямоугольного треугольника равен 6, медиана, опущенная на этот катет, равна 5. Найти гипотенузу этого треугольника.

6. Построить график функции .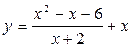

2011г. (I тур), I вариант

1. Решите систему: .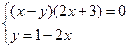

2. Решите неравенство: .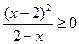

3. При каком а графики функци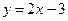й и 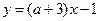не пересекаются?

4. На покупку велосипедов школа выделила 6000 руб. Так как цена велосипеда снизилась на 250 руб., то на эту сумму куплено на 4 велосипеда больше, чем предполагалось. Сколько велосипедов было куплено?

5. На сколько надо увеличить число 252, чтобы 39% от нового числа были бы равны 234.

6. Найти длину стороны ВС в треугольнике АВС, если высота АН, равная 1, образует со сторонами АВ и АС углы в 30º и 45º соответственно.

2011г. (I тур), II вариант

1. Решите систему: .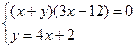

2. Решите неравенство: .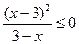

3. При каком а графики функци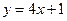й и 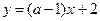не пересекаются?

4. Отец старше дочери в 4 раза. 5 лет назад он был старше её в 9 раз. Сколько сейчас лет отцу и сколько дочери?

5. Цену изделия снизили на 10%. Затем новую цену снизили на 20%. После этого стоимость изделия оказалась равной 72 руб. Найти первоначальную стоимость изделия.

6. Найти длину стороны ВС в треугольнике АВС, если высота АН, равная 1, образует со сторонами АВ и АС углы в 60º и 45º соответственно.

2012г. (I тур), I вариант

1. Решите систему: .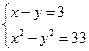

2. Постройте график функции .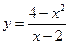

3. Решите неравенство: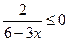

4. Дорогу между двумя городами спрямили, после чего она стала короче на 6%, и теперь её длина 188 км. Определите длину старой дороги.

5. Основания трапеции относятся как 2:3, а средняя линия равна 5м. Найдите основания.

6. Докажите, что число 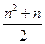является целым, где n – целое число.

2012г. (I тур), II вариант

1. Решите систему: .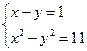

2. Постройте график функции .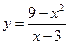

3. Решите неравенство: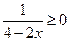

4. Из-за мороза время занятий кружка сократилось на 10% и составило 45 мин. Определите обычное время работы кружка.

5. Средняя линия равнобедренного треугольника, параллельная основанию, равна 3см. Найдите стороны треугольника, если его периметр равен 16 см.

6. Докажите, что число 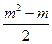является целым, где m – целое число.

Класс

I вариант

(9 класс 1998 г.)

1. Построить график функции: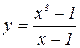

2. Найти наименьшее значение функции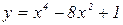

3. В питомнике было 82000 саженцев клёна, что составляло 4% всех саженцев питомника. 85% всех саженцев составляла сосна. Сколько саженцев сосны было в питомнике?

4. Стороны АВ и СD, а также углы A и D четырёхугольника ABCD равны. Докажите равенство углов В и С.

5. Автомобиль проходит первую треть пути со скоростью V 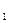, а остальную часть пути – со скоростью V 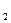=50 км/ч. Определить скорость V 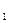, если средняя скорость движения на всем пути V 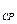=37,5 км/ч.

6. Тело движется по горизонтальной плоскости под действием силы F, направляемой под углом 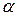к горизонту. При какой величине силы F движение будет равномерно? Коэффициент трения .

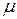II вариант

(9 класс 1998 г.)

1. Решить неравенство: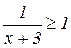

2. Построить график функции: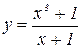

3. Найти наименьшее значение функции: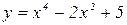

4. Из всех студентов I курса 75 студентов учатся на хорошо и отлично, что составляет 205 всех первокурсников. 4% всех первокурсников – неуспевающие. Сколько неуспевающих студентов на I курсе?

5. Точка начинает движение из состояния покоя и движется по прямой с ускорением а = 0,2 м/с 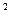. Определить среднюю скорость точки за промежуток времени от t 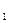= 4 c до t 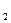= 10 c.

6. Материальная точка массой m = 1,4 кг движется прямолинейно по закону 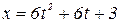. Определить модуль силы, приложенной к точке.

I вариант

(9 класс 1999 г.)

1. Дана функция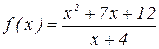

1.1. Решить неравенство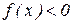

1.2. Решить уравнение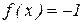

1.3. Построить график функции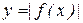

2. Сумма произведения двух чисел и разность их квадратов равны между собой. Найдите эти числа.

3. Катеты прямоугольного треугольника равны а и b. Найти радиусы вписанной и описанной окружностей.

4. Стороны параллелограмма равны а и b. Можно ли около него описать окружность?

5. Сколько секунд должен работать двигатель, который сообщает ракете ускорение 3g, чтобы скорость ракеты в прямолинейном движении возросла с 3 до 5 км/с?

6. На движущемся пароходе мяч бросили вертикально вверх. Куда упадёт мяч, если пароход движется ускоренно?

II вариант

(9 класс 1999 г.)

1. Дана функция .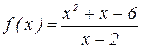

1.1 . Решить неравенство ,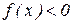

1.2 . Решить уравнение ,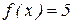

1.3 . Построить график функции .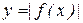

2. Отец старше дочери в 4 раза. Пять лет назад он был старше её в 9 раз. Сколько лет сейчас отцу и дочери?

3. Катет равнобедренного прямоугольного треугольника равен а. Найти радиусы вписанной и описанной окружностей.

4. Стороны параллелограмма равны а и b. Можно ли в него вписать окружность?

5. Самолёт при посадке касается посадочной полосы с горизонтальной скоростью 180 км/ч. После пробега 1000 м самолёт останавливается. Определить модуль среднего замедления самолёта.

6. Куда упадёт мяч, брошенный вертикально вверх на замедленно движущемся пароходе?

II вариант

(9 класс, 2000 г.)

1. Дана функция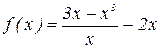

1.1. Сколько целых решений имеет неравенство ?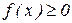

1.2. Построить график функции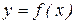

1.3. При каком значении m уравнение 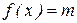имеет ровно два решения?

2. В настоящее время зарплата учителя составляет в среднем 800 руб. На сколько процентов её надо увеличить, чтобы эта зарплата стала 2000 руб.?

3. Внутри квадрата АВСD взята точка Р так, что треугольник АВР - равносторонний. Найдите угол РСD.

4. С каким промежутком оторвались от водосточной трубы две капли, если спустя две секунды после начала падения второй капли расстояние между каплями равно 25 м? Принять g=10 м/с².

5. Тело, массой 10 кг, тянут по горизонтальной поверхности, прикладывая силу 50 Н, направленную под углом 30° к горизонту. Ускорение тела равно 3,5 м/с². Найти коэффициент трения между телом и поверхностью.

I вариант

(9 класс, 2001 г.)

1. Найдите сумму целых решений неравенства: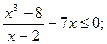

2. Решить систему: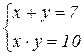

3. Диагонали равнобедренной трапеции перпендикулярны. Найти высоту трапеции, если её средняя линия равна 5.

4. В равнобедренном треугольнике основание и опущенная на него высота равны 4. Найти радиус описанной окружности.

5. Найдите двузначное число, равное сумме чисел его десятков и квадрата числа единиц.

6. При каком а наибольшее значение функции 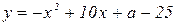равно 3?

II вариант

(9 класс, 2001 г.)

1. Найдите сумму целых решений неравенства: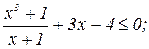

2. Решить систему: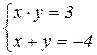

3. В равнобедренной трапеции острый угол равен 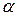, а меньшее основание равно боковой стороне и равно а. Найти высоту трапеции.

4. В равнобедренном треугольнике основание 6 см, а боковая сторона 5 см. Найти радиус окружности, вписанной в треугольник.

5. Трёхзначное число оканчивается цифрой 3. Если эту цифру перенести влево (т.е. поместить вначале), то новое число будет на единицу больше утроенного первоначального числа. Найти это число.

6. При каком а наименьшее значение функции 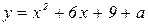равно 2?

II вариант

(9 класс, 2002 г.)

1. Найдите наибольшее целое решение неравенства: .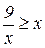

2. При каких а парабола 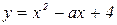касается оси Ох в точке, расположенной правее точки О.

3. Мотоциклист отправился из пункта А в пункт В, отстоящий от А на 120 км. Обратно он выехал с той же скоростью, но через 1 час после выезда должен был остановиться на 10 мин. После этой остановки он продолжал путь до А, увеличив скорость на 6 км/час. Какова была первоначальная скорость мотоциклиста, если известно, что на обратный путь он затратил столько же времени, сколько на путь от А до В?

4. В равнобедренной трапеции основания равны 2 и 6. Диагональ равна 5. Найти периметр и площадь трапеции.

5. В ромб, который делится своей диагональю на 2 равносторонних треугольника, вписан круг. Определите площадь круга, если стороны ромба равны 4 см.

I вариант

(9 класс, 2003г.)

1. Дана функция 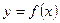, где