Задача Дирихле для уравнения Лапласа – интеграл Пуассона
Уравнению Лапласа удовлетворяет не только потенциал гравитационного поля вне области содержащий источники, но и все его производные вместе с их линейными комбинациями. Этому уравнению в свободном пространстве, т.е. в области, где отсутствуют источники, удовлетворяют и многие другие геофизические поля – компоненты напряженности магнитного поля, естественного электрического, теплового для установившегося температурного режима поля при постоянных электропроводности и теплопроводности среды. Уравнение Лапласа это фундаментальное внеметодное уравнение в геофизике, а функции ему удовлетворяющие называются гармоническими.
Задачей Дирихледля уравнения Лапласа называется задача нахождения значений гармонической функции внутри области по ее граничным – краевым значениям на границе области. Ее также называют задачей аналитического продолжения потенциального поля. Это устоявшееся, но не совсем удачное название. Формально краевая задача Дирихле записывается следующим образом:
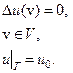
Г – граница области V.
На самом деле для однозначности ее решения необходимо добавление еще дополнительных условий. Однако в некоторых частных случаях достаточно простейших из них.
Частным случаем этой задачи является задача Дирихле для полупространства. Формулируется она следующим образом. Пусть плоскость 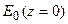 , разбивает все пространство на нижнее
, разбивает все пространство на нижнее 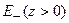 , в котором сконцентрированы все источники поля, и верхнее
, в котором сконцентрированы все источники поля, и верхнее 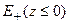 , в котором источники заведомо отсутствуют. Гармоническая в области
, в котором источники заведомо отсутствуют. Гармоническая в области 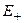 функция
функция 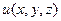 задана своими краевыми значениями на
задана своими краевыми значениями на 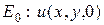 . Считаем, что
. Считаем, что 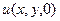 непрерывна на
непрерывна на 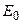 и стремится к нулю на бесконечности. Тогда значения
и стремится к нулю на бесконечности. Тогда значения 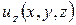 в любой точке области
в любой точке области 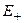 находится по
находится по 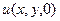 с помощью известного интеграла Пуассона, дающего решение задачи Дирихле для полупространства:
с помощью известного интеграла Пуассона, дающего решение задачи Дирихле для полупространства:
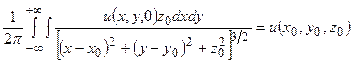 | (2.6) |
.
В двухмерном случае интеграл Пуассона имеет вид:
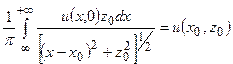 | (2.6а) |
Каждое из приведенных соотношений может быть также как и ранее, записано в операторной форме:
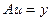 . . | (2.7) |
Расчет интеграла Пуассона, как для двухмерного, так и для трехмерного случаев является типичной задачей из области решения уравнений математической физики. Она не содержит «подводных камней». Она имеет решение, это решение единственно и устойчиво зависит от начальных данных во всех имеющих смысл нормах. Степень гладкости продолженного поля, т.е. 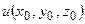 для (6) всегда выше, чем степень гладкости краевых значений
для (6) всегда выше, чем степень гладкости краевых значений 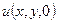 . Мы пока обращаемся к интуитивному пониманию смысла гладкости. Однако, эта задача может рассматриваться и как обратная задача – нахождения по известному
. Мы пока обращаемся к интуитивному пониманию смысла гладкости. Однако, эта задача может рассматриваться и как обратная задача – нахождения по известному 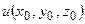 или
или 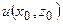 на некотором множестве в
на некотором множестве в 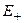 значения этих функций на
значения этих функций на 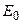 . В операторной постановке (7) это соответствует расчету величины u под знаком оператора A по заданной правой части y. При попытке решения этой обратной задачи возникает целый «букет» неприятностей, которые почти очевидны. Они начинаются с того, что совсем не факт, что решение будет существовать для конкретных данных. И уже совершенно очевиден факт, что гладкость результата будет ниже, и даже катастрофически ниже гладкости исходных данных. Решение будет неустойчиво, разваливаться от малейших вариаций исходных данных. Это проявление тех же эффектов, предупреждение о которых было сделано выше
. В операторной постановке (7) это соответствует расчету величины u под знаком оператора A по заданной правой части y. При попытке решения этой обратной задачи возникает целый «букет» неприятностей, которые почти очевидны. Они начинаются с того, что совсем не факт, что решение будет существовать для конкретных данных. И уже совершенно очевиден факт, что гладкость результата будет ниже, и даже катастрофически ниже гладкости исходных данных. Решение будет неустойчиво, разваливаться от малейших вариаций исходных данных. Это проявление тех же эффектов, предупреждение о которых было сделано выше
