Дифференциалы высших порядков
Будем рассматривать dx в выражении для dy как постоянный множитель.Тогда функция dy представляет собой функцию только аргумента x и ее дифференциал в точке x имеет вид (при рассмотрении дифференциала от dy будем использовать новые обозначения для дифференциалов):
δ (d y) = δ [f ' (x) d x] = [f ' (x) d x] ' δx = f '' (x) d(x) δx .
Дифференциал δ (d y) от дифференциала dy в точке x, взятый при δx = dx, называется дифференциалом второго порядка функции f (x) в точке x и обозначается d2y, т.е.
d2y = f ''(x)·(dx)2.
В свою очередь, дифференциал δ(d2y) от дифференциала d2y, взятый при δx = dx, называется дифференциалом третьего порядка функции f(x) и обозначается d3y и т.д. Дифференциал δ(dn-1y) от дифференциала dn-1f, взятый при δx = dx, называется дифференциалом n - го порядка (или n - м дифференциалом) функции f(x) и обозначается dny.
Докажем, что для n - го дифференциала функции справедлива формула
dny = y(n)·(dx)n, n = 1, 2, … (3.1)
При доказательстве воспользуемся методом математической индукции. Для n = 1 и n = 2 формула (3.1) доказана. Пусть она верна для дифференциалов порядка n - 1
dn−1y = y(n−1)·(dx)n−1,
и функция y(n-1)(x) дифференцируема в некоторой точке x. Тогда
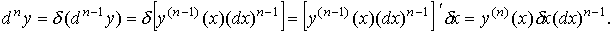
Полагая δx = dx, получаем
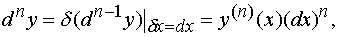
что и требовалось доказать.
Для любого n справедливо равенство
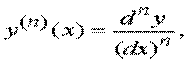 или
или 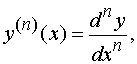
т.е. n - я производная функции y = f ( x ) в точке x равна отношению n - го дифференциала этой функции в точке x к n - й степени дифференциала аргумента.
36) Ферма:
Для любого натурального числа 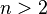 уравнение
уравнение
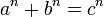
не имеет натуральных решений  ,
,  и
и  .
.
Ролль: Если вещественная функция, непрерывная на отрезке 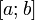 и дифференцируемая на интервале
и дифференцируемая на интервале 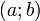 , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
, принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Док-во
Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала.
Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма, в этой точке производная равна 0.
37) Теорема Коши́ о среднем значении.
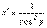 . Следовательно, y ' = cos2 y . Но
. Следовательно, y ' = cos2 y . Но 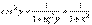 .Поэтому
.Поэтому 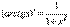 6.
6. 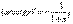 7. Используя эти формулы, найти производные следующих функций:
7. Используя эти формулы, найти производные следующих функций: 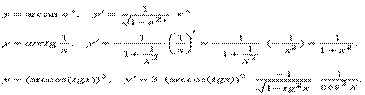 31) 1.8. Производная показательно степенной функции Рассмотрим показательно степенную функцию y = u(x)v(x) Теорема 11. Пусть функции u = u(x), v = v(x) дифференцируемы, тогда функция y = u(x)v(x) дифференцируема и
31) 1.8. Производная показательно степенной функции Рассмотрим показательно степенную функцию y = u(x)v(x) Теорема 11. Пусть функции u = u(x), v = v(x) дифференцируемы, тогда функция y = u(x)v(x) дифференцируема и 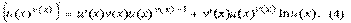 Доказательство Так как ln y = v(x) ln u(x), то, продифференцировав это равенство, получаем
Доказательство Так как ln y = v(x) ln u(x), то, продифференцировав это равенство, получаем 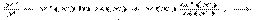
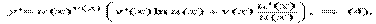 Теорема доказана. 32) Дифференциалом функции
Теорема доказана. 32) Дифференциалом функции 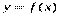 в точке
в точке 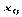 называется главная часть ее приращения, равная произведению производной функции на приращение аргумента. .
называется главная часть ее приращения, равная произведению производной функции на приращение аргумента. . 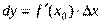 Геометрический и механический смысл дифференциала 1. Проведем к графику функции
Геометрический и механический смысл дифференциала 1. Проведем к графику функции 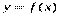 касательную
касательную 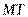 в точке
в точке 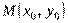 и рассмотрим ординату касательной для точки
и рассмотрим ординату касательной для точки 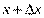 (Рис. 32).
(Рис. 32). 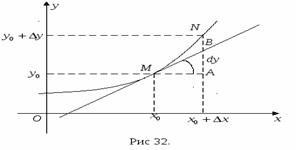 Из рисунка
Из рисунка 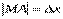 ,
, 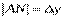 , из прямоугольного треугольника
, из прямоугольного треугольника 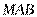 имеем:
имеем: 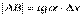 . Но согласно геометрическому смыслу производной получаем
. Но согласно геометрическому смыслу производной получаем 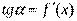 ,
, 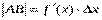 . Таким образом, дифференциал функции в точке равен приращению ординаты касательной к графику функции в этой точке, когда точка получает приращение. Механический смысл дифференциала заключается в том, что дифференциал пути равен приращению пути, полученному в предположении, что, начиная с данного момента времени
. Таким образом, дифференциал функции в точке равен приращению ординаты касательной к графику функции в этой точке, когда точка получает приращение. Механический смысл дифференциала заключается в том, что дифференциал пути равен приращению пути, полученному в предположении, что, начиная с данного момента времени 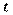 , точка движется равномерно, сохраняя приобретенную скорость. Свойства Дифференциалов 1. Дифференциал постоянной равен нулю: dc = 0, с = const. 2. Дифференциал суммы дифференцируемых функцийравен сумме дифференциалов слагаемых: d(u+v)=du + dv Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const). 3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой: d(uv) = udv + vdu. Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const). 4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
, точка движется равномерно, сохраняя приобретенную скорость. Свойства Дифференциалов 1. Дифференциал постоянной равен нулю: dc = 0, с = const. 2. Дифференциал суммы дифференцируемых функцийравен сумме дифференциалов слагаемых: d(u+v)=du + dv Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны d(u+c) = du (c= const). 3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой: d(uv) = udv + vdu. Следствие. Постоянный множитель можно выносить за знак дифференциала d(cu) = cdu (с = const). 4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой 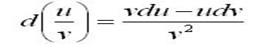 5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной. Приближенные вычисления с помощью дифференциала функции одной переменной В первом параграфе рулит функция одной переменной. Как все знают, она обозначается через
5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной. Приближенные вычисления с помощью дифференциала функции одной переменной В первом параграфе рулит функция одной переменной. Как все знают, она обозначается через 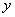 или через
или через 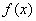 . Для данной задачи намного удобнее использовать второе обозначение. Сразу перейдем к популярному примеру, который часто встречается на практике: Вычислить приближенно
. Для данной задачи намного удобнее использовать второе обозначение. Сразу перейдем к популярному примеру, который часто встречается на практике: Вычислить приближенно 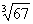 , заменяя приращения функции ее дифференциалом. Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
, заменяя приращения функции ее дифференциалом. Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала: 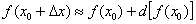 Начинаем разбираться, здесь всё просто! На первом этапе необходимо составить функцию
Начинаем разбираться, здесь всё просто! На первом этапе необходимо составить функцию 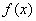 . По условию предложено вычислить кубический корень из числа:
. По условию предложено вычислить кубический корень из числа: 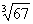 , поэтому соответствующая функция имеет вид:
, поэтому соответствующая функция имеет вид: 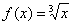 . Нам нужно с помощью формулы найти приближенное значение
. Нам нужно с помощью формулы найти приближенное значение 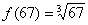 . Смотрим на левую часть формулы
. Смотрим на левую часть формулы 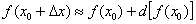 , и в голову приходит мысль, что число 67 необходимо представить в виде
, и в голову приходит мысль, что число 67 необходимо представить в виде 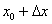 . Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе: 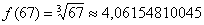 – получилось 4 с хвостиком, это важный ориентир для решения. В качестве
– получилось 4 с хвостиком, это важный ориентир для решения. В качестве 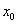 подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение
подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение 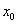 должно быть как можно ближе к 67. В данном случае:
должно быть как можно ближе к 67. В данном случае: 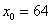 . Действительно:
. Действительно: 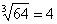 . Примечание: Когда с подбором
. Примечание: Когда с подбором  всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае
всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае 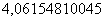 ), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае
), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае 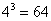 ). В результате и будет выполнен нужный подбор:
). В результате и будет выполнен нужный подбор: 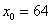 . Пусть даны две функции
. Пусть даны две функции 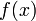 и
и 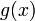 такие, что: 1.
такие, что: 1. 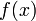 и
и 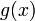 определены и непрерывны на отрезке
определены и непрерывны на отрезке 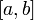 ; 2. производные
; 2. производные 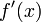 и
и 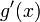 конечны на интервале
конечны на интервале 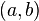 ; 3. производные
; 3. производные 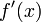 и
и 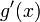 не обращаются в нуль одновременно на интервале
не обращаются в нуль одновременно на интервале 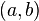 4.
4. 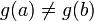 ; тогда существует
; тогда существует 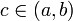 , для которой верно:
, для которой верно: 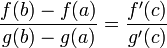 . (Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале
. (Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале 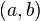 .) Геометрически это можно переформулировать так: если
.) Геометрически это можно переформулировать так: если 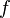 и
и 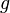 задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр
задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр 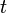 ), то на любом отрезке такой кривой, заданном параметрами
), то на любом отрезке такой кривой, заданном параметрами 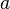 и
и 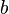 , найдётся касательный вектор, коллинеарный вектору перемещения от
, найдётся касательный вектор, коллинеарный вектору перемещения от 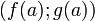 до
до 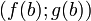 . Доказательство Для доказательства введём функцию
. Доказательство Для доказательства введём функцию 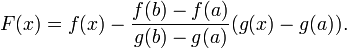 |
Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны 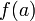 . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции 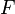 равна нулю, а
равна нулю, а 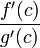 равна как раз необходимому числу.
равна как раз необходимому числу.
Лагра́нжа
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция 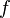 непрерывна на отрезке
непрерывна на отрезке 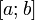 и дифференцируема в интервале
и дифференцируема в интервале 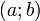 , то найдётся такая точка
, то найдётся такая точка 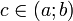 , что
, что
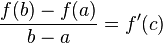 .
.
Геометрически это можно переформулировать так: на отрезке 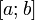 найдётся точка, в которой касательнаяпараллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
найдётся точка, в которой касательнаяпараллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое истолкование: Пусть 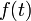 — расстояние точки в момент
— расстояние точки в момент 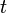 от начального положения. Тогда
от начального положения. Тогда 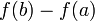 есть путь, пройденный с момента
есть путь, пройденный с момента 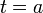 до момента
до момента 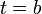 , отношение
, отношение 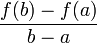 — средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени
— средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени 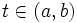 , то в некоторый момент она будет равна своему среднему значению на этом участке.
, то в некоторый момент она будет равна своему среднему значению на этом участке.
Доказательство
Для функции одной переменной:
Введем функцию 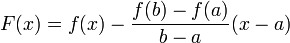 . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны
. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны 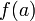 . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции 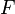 равна нулю:
равна нулю:
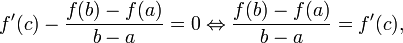
что и требовалось доказать.
38)Правило Бернулли-Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 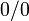 и
и 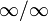 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия:
1. 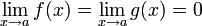 или
или 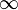 ;
;
2. 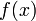 и
и 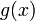 дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности 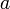 ;
;
3. 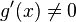 в проколотой окрестности
в проколотой окрестности 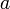 ;
;
4. существует 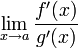 ,
,
тогда существует 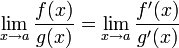 .
.
Пределы также могут быть односторонними.
Наши рекомендации
