ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ. Перед выполнением контрольной работы рекомендуется изучить теорию, необходимую для выполнения работы

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Перед выполнением контрольной работы рекомендуется изучить теорию, необходимую для выполнения работы, и ответить на вопросы для самопроверки.

Вопросы для самопроверки

Дайте определения:

1. вектора и модуля вектора;

2. коллинеарности, компланарности, равенства векторов;

3. линейных операций над векторами; *)

4. базиса на прямой, на плоскости и в пространстве;

5. линейной зависимости и независимости векторов;

6. скалярного произведения векторов; *)

7. ортонормированного базиса;

8. векторного произведения векторов; *)

9. смешанного произведения трех векторов; *)

10. определителей 2-го и 3-го порядков; *)

11. полярной, цилиндрической и сферической систем координат.

12. Как выражаются введенные операции над векторами через их координаты в ортонормированном базисе?

13. Как преобразуются координаты вектора при замене базиса пространства (плоскости)?

14. Какому условию должны удовлетворять координаты трех векторов, чтобы их можно было принять за базис пространства?

15. Как можно найти точку пересечения а) двух линий на плоскости? б) трех поверхностей? в) линии и поверхности?

16. Опишите параметрический способ задания линий и поверхностей.

Напишите:

17. векторное уравнение плоскости, имеющей заданную нормаль и проходящей через заданную точку;

18. векторное уравнение прямой, имеющей заданный направляющий вектор и проходящей через заданную точку;

19. уравнения прямой, проходящей через две точки, в пространстве и на плоскости;

20. уравнение плоскости, проходящей через три заданные точки;

21. формулы вычисления углов а) между двумя прямыми (на плоскости и в пространстве), б) между двумя плоскостями, в) между прямой и плоскостью;

22. условия параллельности и перпендикулярности двух прямых ( на плоскости и в пространстве), двух плоскостей, прямой и плоскости;

23. канонические уравнения эллипса, гиперболы, параболы; уравнения асимптот гиперболы;

24. канонические уравнения поверхностей 2-го порядка;

25. примеры уравнений линий в полярных координатах;

Дайте определения:

26. матрицы; линейных операций с матрицами; *)

27. определителя; *) минора, алгебраического дополнения;

28. решения системы линейных уравнений, совместности и несовместности системы.

29. Сформулируйте теорему Кронекера – Капелли.

30. Напишите формулы Крамера и дайте условие их применимости.

31. При каком условии однородная система линейных уранений с квадратной матрицей имеет ненулевое решение?

32. Опишите метод Гаусса решения систем линейных уравнений и отыскания ранга матрицы.

Дайте определения:

33. ранга матрицы;

34. свободных и базисных неизвестных в системе линейных уравнений;

35. общего решения однородной и неоднородной линейной системы;

36. произведения двух матриц; *)

37. обратной матрицы;

38. линейного (векторного ) пространства Lⁿ;

39. линейной зависимости и независимости векторов в Lⁿ;

40. базиса и размерности линейного пространства Lⁿ;

41. векторной формы записи системы линейных уравнений;

42. евклидова пространства ;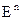

43. модуля вектора и угла между векторами в евклидовом пространстве ;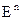

44. линейного преобразования пространства и его матрицы;

45. композиции линейных преобразований и ее матрицы;

46. собственных значений и собственных векторов линейного преобразования;

47. квадратичной формы и ее матрицы.

48. Как применяется теория квадратичных форм для приведения уравнений линий и поверхностей 2-го порядка к каноническому виду?

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

1.Найти координаты вектора xв базисе {a,b,c}:

Указание: при решении системы применить правило Крамера.

1.1. x={ -2, 4, 7 },a={ 0, 1, 2 },b={ 1, 0, 1 }, c={ -1, 2, 4 }.

1.2. x={ 6, 12, -1 },a={ 1, 3, 0 },b={ 2, -1, 1 }, c={ 0, -1, 2 }.

1.3. x={ 1, -4, 4 },a={ 2, 1, -1 },b={ 0, 3, 2 }, c={ 1, -1, 1 }.

1.4. x={ -9, 5, 5 },a={ 4, 1, 1 },b={ 2, 0, -3 }, c={ -1, 2, 1 }.

1.5. x={ -5, -5, 5 },a={ -2, 0, 1 },b={ 1, 3, -1 }, c={ 0, 4, 1 }.

1.6. x={ 13, 2, 7 }, a={ 5, 1, 0 },b={ 2, -1, 3 }, c={ 1, 0, -1 }.

1.7. x={-19, -1, 7 }, a={ 0, 1, 1 },b={ -2, 0, 1 }, c={ 3, 1, 0 }.

1.8. x={ 3, -3, 4 },a={ 1, 0, 2 },b={ 0, 1, 1 }, c={ 2, -1, 4 }.

1.9. x={ 3, 3, -1 },a={ 3, 1, 0 },b={ -1, 2, 1 }, c={ -1, 0, 2 }.

1.10. x={ -1, 7, -4 },a={ -1, 2, 1 },b={ 2, 0, 3 }, c={ 1, 1, -1 }.

1.11. x={ 6, 5, -14 },a={ 1, 1, 4 },b={ 0, -3, 2 }, c={ 2, 1, -1 }.

1.12. x={ 6, -1, 7 },a={ 1, -2, 0 },b={ -1, 1, 3 }, c={ 1, 0, 4 }.

1.13. x={ 5, 15, 0 },a={ 1, 0, 5 },b={ -1, 3, 2 }, c={ 0, -1, 1 }.

1.14. x={ 2, -1, 11 },a={ 1, 1, 0 },b={ 0, 1, -2 }, c={ 1, 0, 3 }.

1.15. x={ 11, 5, -3 },a={ 1, 0, 2 },b={ -1, 0, 1 }, c={ 2, 5, -3 }.

1.16. x={ 8, 0, 5 },a={ 2, 0, 1 },b={ 1, 1, 0 }, c={ 4, 1, 2 }.

1.17. x={ 3, 1, 8 },a={ 0, 1, 3 },b={ 1, 2, -1 }, c={ 2, 0, -1 }.

1.18. x={ 8, 1, 12 },a={ 1, 2, -1 },b={ 3, 0, 2 }, c={ -1, 1, 1 }.

1.19. x={ -9, -8, -3 },a={ 1, 4, 1 },b={ -3, 2, 0 }, c={ 1, -1, 2 }.

1.20. x={ -5, 9, -13 },a={ 0, 1, -2 },b={ 3, -1, 1 }, c={ 4, 1, 0 }.

1.21. x={ 2, 7, 5 },a={ 1, 0, 1 },b={ 1, -2, 0 }, c={ 0, 3, 1 }.

1.22. x={ 15, -20, -1 },a={ 0, 2, 1 },b={ 0, 1, -1 }, c={ 5, -3, 2 }.

1.23 х={ 10, 1, 11 }, a ={ 3, 1, -1}, b={ 1, -1, 4}, c={ 2, 1, 5}

1.24 x={ 0, 6, -1}, a ={ -1, 2, 1}, b ={ 2, 1, -1}, c={ 1, 2, 2}

2.Даны координаты вершин тетраэдра А₁ А₂ А₃ А₄ . Найти:

1) длину ребра А₁ А₂ ;

2) угол между ребрами А₁ А₂ и А₁ А₄ ;

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃ ;

4) площадь грани А₁ А₂ А₃ ;

5) объем тетраэдра;

6) уравнения прямой А₁А₂ ;

7) уравнение плоскости А₁ А₂ А₃ ;

8) уравнения высоты, опущенной из вершиныА₄ на грань А₁ А₂ А₃ ;

9) расстояние вершины А₄ до грани А₁ А₂ А₃ ;

10) расстояние вершины А₄до ребра А₁ А₂ .

Указание: все результаты представить точно в виде радикалов, а затем привести их приближенные значения.

А₁А₂ А₃А₄

2.1.( 1, 3, 6 ) ( 2, 2, 1 ) ( -1, 0, 1 ) ( -4, 6, -3 )

2.2.( -4, 2, 6 ) ( 2, -3, 0 ) ( -10, 5, 8 ) ( -5, 2, -4 )

2.3.( 7, 2, 4 ) ( 7, -1, -2 ) ( 3, 3, 1 ) ( -4, 2, 1 )

2.4.( 2, 1, 4 ) ( -1, 5, -2 ) ( -7, -3, 2 ) ( -6, -3, 6 )

2.5.( -1, -5, 2 ) (-6, 0, -3 ) ( 3, 6, -3 ) (-10, 6, 7 )

2.6.( 0, -1, -1 ) ( -2, 3, 5 ) ( 1, -5, -9 ) ( -1, -6, 3 )

2.7.( 5, 2, 0 ) ( 2, 5, 0 ) ( 1, 2, 4 ) ( -1, 1, 1 )

2.8.( 2, -1, -2 ) ( 1, 2, 1 ) ( 5, 0, -6 ) ( -10, 9, -7)

2.9.(-2, 0, -4 ) ( -1, 7, 1 ) ( 4, -8, - 4 ) ( 1, - 4, 6 )

2.10.( 14, 4, 5 ) (-5, -3, 2 ) ( -2, -6, -3 ) ( -2, 2, -1 )

2.11.( 1, 2, 0 ) ( 3, 0, -3 ) ( 5, 2, 6 ) ( 8, 4, -9 )

2.12.( 2, -1, 2 ) ( 1, 2, -1 ) ( 3, 2, 1 ) ( -4, 2, 5 )

2.13.( 1, 1, 2 ) ( -1, 1, 3 ) ( 2, -2, 4 ) ( -1, 0, -2 )

2.14.( 2, 3, 1 ) ( 4, 1, -2 ) ( 6, 3, 7 ) ( 7, 5, -3 )

2.15.( 1, 1, -1 ) ( 2, 3, 1 ) ( 3, 2, 1 ) ( 5, 9, -8 )

2.16.( 1, 5, -7 ) (-3, 6, 3 ) ( -2, 7, 3 ) ( -4, 8, -12 )

2.17.( -3, 4, -7 ) ( 1, 5, -4 ) ( -5, -2, 0 ) ( 2, 5, 4 )

2.18.( -1, 2, -3 ) ( 4, -1, 0 ) ( 2, 1, -2 ) ( 3, 4, 5 )

2.19.( 4, -1, 3 ) ( -2, 1, 0 ) ( 0, -5, 1 ) ( 3, 2, -6 )

2.20.( 1, -1, 1 ) ( -2, 0, 3 ) ( 2, 1, -1 ) ( 2, -2, -4 )

2.21.( 2, -4, -3 ) ( 5, -6, 0 ) ( -1, 3, -3 ) ( -10, -8, 7 )

2.22.( 1, -1, 2 ) ( 2, 1, 2 ) ( 1, 1, 4 ) ( 6, -3, 8 )

2.23.( -1, 2, 4) ( -1, -2, -4 ) ( 3, 0, -1 ) ( 7, -3, 1 )

2.24.( 0, -3, 1 ) ( -4, 1, 2 ) ( 2, -1, 5 ) ( 3, 1, -4 )

3.Линия задана уравнением 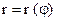в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от =0 до =2 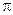с шагом 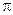/8 ;

2) найти уравнение данной линии в декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;

3) по уравнению в декартовых координатах определить, какая это линия.

3.1. r=2/(1+cos ). 3.2. r=4/(2-3cos ). 3.3. r=1/(2-2cos ).

3.4. r=10/(2+cos ). 3.5. r=1/(2+2cos ). 3.6. r=1/(2+3cos ).

3.7. r=5/(2-cos ). 3.8. r=8/(3-cos ). 3.9. r=2/(3-4cos ).

3.10. r=5/(1-2cos ). 3.11 r=4/(3+cos ). 3.12. r=6/4+3cos ).

3.13. r=2/(2+5cos ). 3.14. r=3/(3+4cos ). 3.15. r=2/(3-2cos ).

3.16. r=3/(5-2cos ). 3.17. r=3/(2+4cos ). 3.18. r=5/(2-3cos ).

3.19. r=1/(4-cos ) 3.20. r=1/(3+cos ). 3.21. r=4/(1-cos ).

3.22. r=2/(5-3cos ). 3.23. r=1/(2-3cos ). 3.24. r=6(1+cos ) .

4.Решить систему уравнений:

1) методом Гаусса;

2) средствами матричного исчисления ( x=A_{_}^-1 B ) ;

Указание: вычисления проводить с обычными дробями, не используя десятичных приближений.

4.1.	х1 – х2 + 7х3 = 6 2х1 + 3х2 - 3х3 = 10 3х1 + 2х2 + 5х3 =17	4.2.	4х1 +9х2 + 2х3 = 1 7х1 + х2 - 4х3 = -13 8х1 + 3х2 - х3 = -13	4.3.	8х1 + 4х2 + 3х3 = 7 2х1 + 6х2 - 2х3 = 4 3х1 +10х2 + х3 = 11
4.4.	10х1 + х2 + 3х3 = 19 3х1 + 4х2 + 9х3 = 30 х1 + 2х2 + 2х3 = 7	4.5.	2х1 + х2 + 5х3 = 24 4х1 + 3х2 + 3х3 = 20 х1 + 6х2 + х3 = 6	4.6.	х1 + 3х2 + 4х3 = 7 7х1 + 4х2 + 8х3 = 32 3х1 + 2х2 + 5х3 = 14
4.7.	х1 + 4х2 + 6х3 = 14 -2х1 +7х2 + 4х3 = 18 3х1 + 2х2 + 2х3 = 6	4.8.	х1 + 6х2 + 3х3 = 21 4х1 + 8х2 + х3 = 18 3х1 + 5х2 + 4х3 = 33	4.9.	2х1 + 3х2 + 2х3 = 16 7х1 + х2 - 7х3 = 14 3х1 + 8х2 + 4х3 = 27
4.10.	7х1 + 4х2 + 3х3 = 2 2х1 + 3х2 + 4х3 = -5 х1 + 5х2 - 2х3 = -13	4.11.	3х1 + 2х2 + х3 = 5 2х1 + 3х2 + х3 = 1 2х1 + х2 + 3х3 = 11	4.12.	х1 - 2х2 + 3х3 = 6 2х1 + 3х2 - 4х3 = 20 3х1 - 2х2 - 5х3 = 6
4.13.	4х1 – 3х2 + 2х3 = 9 2х1 + 5х2 - 3х3 = 4 5х1 + 6х2 - 2х3 = 18	4.14.	х1 + х2 + 2х3 = -1 2х1 - х2 + 2х3 = - 4 4х1 + х2 + 4х3 = - 2	4.15.	2х1 - х2 - х3 = 4 3х1 + 4х2 - 2х3 = 11 3х1 - 2х2 + 4х3 = 11
4.16.	3х1 + 4х2 + 2х3 = 8 2х1 - х2 - 3х3 = - 4 х1 + 5х2 + х3 = 0	4.17.	х1 + х2 - х3 = 1 8х1 + 3х2 - 6х3 = 2 4х1 + х2 - 3х3 = 3	4.18.	х1 - 4х2 - 2х3 = - 3 3х1 + х2 + х3 = 5 3х1 - 5х2 - 6х3 = -9
4.19.	7х1 – 5х2 = 31 4х1 + 11х3 = - 43 2х1 3х2 + 4х3 = -20	4.20.	х1 + 2х2 + 4х3 = 31 5х1 + х2 + 2х3 = 20 3х1 - х2 + х3 = 9	4.21.	5х1 + 3х2 - х3 = 4 х1 + 5х2 + 5х3 = 12 3х1 + 4х2 - 2х3 = - 4
4.22.	3х1 + 4х3 = - 5 х1 + 2х2 = 3 х1 + х2 + х3 = 1	4.23.	2x1 + x2 - x3 = 5 x1 + 2x2 +x3 = 1 3x1 - x2 + x3 = 0	4.24.	x1 + 2x2 +2x2 = 9 2x1 - x2 +2x3 = 4 3x1 + x2 - x3 = 3

5.Найти какой-нибудь базис и определить размерность линейного пространства решений системы:

5.1.3x₁ + x₂ - 8x₃ + 2x₄ + x₅ = 0 5.2.7x₁ + 2x₂ - x₃ - 2x₄ + 2x₅ = 0

2x₁ - 2x₂ - 3x₃ - 7x₄ + 2x₅ = 0 x₁ - 3x₂ + x₃ - x₄ - x₅ = 0

x₁ + 11x₂ - 12x₃ + 34x₄ - 5x₅ = 0 2x₁ + 5x₂ + 2x₃ + x₄ + x₅ = 0

5.3.x₁ + x₂ + 10x₃ + x₄ - x₅ = 0 5.4.6x₁ - 9x₂ + 21x₃ - 3x₄ - 12x₅ = 0

5x₁ - x₂ + 8x₃ - 2x₄ + 2x₅ = 0 -4x₁ + 6x₂ - 14x₃ + 2x₄ + 8x₅ = 0

3x₁ - 3x₂ - 12x₃ - 4x₄ + 4x₅ = 0 2x₁ - 3x₂ + 7x₃ - x₄ - 4x₅ = 0

5.5.2x₁ - x₂ + 2x₃ - x₄ + x₅ = 0 5.6.5x₁ - 2x₂ + 3x₃ - 4x₄ - x₅ = 0

x₁ + 10x₂ - 3x₃ - 2x₄ - x₅ = 0 x₁ + 4x₂ - 3x₃ + 2x₄ - 5x₅ = 0

4x₁ + 19x₂ - 4x₃ - 5x₄ - x₅ = 0 6x₁ + 2x₂ - 2x₄ - 6x₅ = 0

5.7.12x₁ - x₂ + 7x₃ + 11x₄ - x₅ = 0 5.8.x₁ + 2x₂ + x₃ + 4x₄ + x₅ = 0

24x₁- 2 x₂ + 14x₃ + 22x₄ -2x₅ = 0 2x₁ - x₂ + 3x₃ + x₄ - 5x₅ = 0

x₁ + x₂ + x₃ - x₄ + x₅ = 0 x₁ + 3x₂ - x₃ - 6x₄ - x₅ = 0

5.9.2x₁ - x₂ + 3x₃ - x₄ - x₅ = 0 5.10.x₁ + x₂ + x₃ + 2x₄ + x₅ = 0

x₁ + 5x₂ - x₃ + x₄ + 2x₅ = 0 x₁ - 2x₂ - 3x₃ + x₄ - x₅ = 0

x₁ + 16x₂ - 6x₃ + 4x₄ + 7x₅ = 0 2x₁ - x₂ - 2x₃ + 3x₄ = 0

5.11.8x₁ + x₂ + x₃ - x₄ + 2x₅ = 0 5.12.x₁ + 3x₂ - x₃ + 12x₄ - x₅ = 0

3x₁ - 3x₂ - 2x₃ + x₄ - 3x₅ = 0 2x₁ - 2x₂ + x₃ - 10x₄ + x₅ = 0

5x₁ + 4x₂ + 3x₃ - 2x₄ + 5x₅ = 0 3x₁ + x₂ + 2x₄ = 0

5.13.7x₁ - 14x₂ + 3x₃ - x₄ + x₅ = 0 5.14.x₁ + 2x₂ + 3x₃ + x₄ - x₅ = 0

x₁ - 2x₂ + x₃ - 3x₄ + 7x₅ = 0 2x₁ - 2x₂ - 5x₃ - 3x₄ + x₅ = 0

5x₁ - 10x₂ + x₃ + 5x₄ - 13x₅ = 0 3x₁ - 2x₂ + 3x₃ + 2x₄ - x₅ = 0

5.15.x₁ + x₂ + x₃ - x₄ - x₅ = 0 5.16.2x₁ + x₂ - 3x₃ + x₄ - x₅ = 0

2x₁ + x₂ - 2x₃ - x₄ - 2x₅ = 0 3x₁ - x₂ + 2x₃ - x₄ + 2x₅ = 0

x₁ + 2x₂ + 5x₃ - 2x₄ - x₅ = 0 x₁ - 2x₂ + 5x₃ - 2x₄ + 3x₅ = 0

5.17.x₁ + 2x₂ - 3x₃ + 10x₄ -x₅ = 0 5.18.2x₁ + x₂ - x₃ + 7x₄ + 5x₅ = 0

x₁ - 2x₂ + 3x₃ - 10x₄ + x₅ = 0 x₁ - 2x₂ + 3x₃ - 5x₄ - 7x₅ = 0

x₁ + 6x₂ - 9x₃ + 30x₄ - 3x₅ = 0 3x₁ - x₂ + 2x₃ + 2x₄ - 2x₅ = 0

5.19.2x₁ - 2x₂ - 3x₃ - 7x₄ + 2x₅ = 0 5.20.3x₁ + x₂ - 8x₃ + 2x₄ + x₅ = 0

x₁ + 11x₂ - 12x₃+ 34x₄ - 5x₅ = 0 x₁ + 11x₂ -12x₃ - 34x₄ - 5x₅ = 0

x₁ - 5x₂ + 2x₃ - 16x₄ + 3x₅ = 0 x₁ - 5x₂ + 2x₃ - 16x₄ + 3x₅ = 0

5.21.3x₁ + 2x₂ - 2x₃ - x₄ + 4x₅ = 0 5.22x₁ + x₂ +3x₃ - 2x₄ +3x₅ = 0

7x₁ + 5x₂ - 3x₃ - 2x₄ + x₅ = 0 2x₁ + 2x₂ + 4x₃ – x₄ +3x₅ = 0

x₁ + x₂ + x₃ - 7x₅ = 0 x₁ + x₂ + 5x₃ – 5x₄ + 6x₅ = 0

5.23 x₁ + 2x₂ + 3x₃ – 2x₄ +x₅ = 0 5.24x₁ + x₂ + x₃ + 2x₄ +x₅ = 0

x₁ + 2x₂ + 7x₃ – 4x₄ +x₅ = 0 x₁ – 2x₂ – 3x₃ +x₄ – x₅ = 0

x₁ + 2x₂ + 11x₃ – 6x₄ + x₅ = 0 2x₁ – x₂ – 2x₃ + 3x₄ = 0

Пример решения: 5x₁ + 2x₂ - x₃ + 3x₄ + 4x₅ = 0

3x₁ + x₂ - 2x₃ + 3x₄ + 5x₅ = 0

6x₁ + 3x₂ - 2x₃ + 4x₄ + 7x₅ = 0

Выпишем матрицу системы, нумеруя столбцы ( нумеровать строки необязательно):

5 2 -1 3 4

3 1 -2 3 5

6 3 -2 4 7

_{(1) (2) (3) (4) (5)}

и приведем ее к каноническому виду, применяя элементарные преобразования: умножение строки на число, перестановку строк, сложение строк, те же операции со столбцами. При этом следим за переставляемыми столбцами по их номерам.

1) Расположим в левом верхнем углу элемент, равный 1. (Если такого элемента в матрице нет, то следует поделить любой столбец на любой отличный от 0 его элемент). Для этого поменяем местами строки (1) и (2):

3 1 -2 3 5

5 2 -1 3 4

6 3 -2 4 7

_{(1) (2) (3) (4) (5)}

Теперь поменяем столбцы (1) и (2):

1 3 -2 3 5 [-2], [-3]

2 5 -1 3 4

3 6 -2 4 7

_{(2) (1) (3) (4) (5)}

В дальнейшем 1-я строка не подлежит изменению!

2) Сформируем нули во 2-й и 3-й строках первого столбца. Для этого умножим 1-ю строку на 1-й элемент 2-й строки и вычтем из 2-й строки. Так же поступим с 3-й строкой. (Множители указаны в [ ] .)

1 3 -2 3 5

0 -1 3 -3 - 6 [ -1]

0 -3 4 -5 -8

_{(2) (1) (3) (4) (5)}

В дальнейшем 1-й столбец не подлежит изменению!

3) Превратим в «1» 2-й элемент на главной диагонали, то есть стоящий во 2-й строке и 2-ом столбце. В нашем примере достаточно умножить на (-1) вторую строку. (В общем случае следует поделить 2-ю строку на этот элемент. Если же он равен 0, то предварительно переставляют строки не трогая 1-й (!), или столбцы не трогая 1-й (!).)

1 3 -2 3 5

0 1 - 3 3 6 [ 3 ]

0 -3 4 -5 -8

_{(2) (1) (3) (4) (5)}

В дальнейшем 2-я строка не подлежит изменению!

4) Превратим в «0» 3-й элемент 2-го столбца. Для этого умножим 2-ю строку на (+3) и сложим с 3-ей.

[ 1 3 -2 ] 3 5

[ 0 1 - 3 ] 3 6

[ 0 0 - 5 ] 4 10

_{(2) (1) (3) (4) (5)}

Под главной диагональю стоят нули, а на самой главной диагонали их нет. Этот вид и является каноническим. (В других вариантах 3-я строка, или даже 2-я и 3-я вместе, могут состоять из одних нулей.) Минор, содержащий ненулевые элементы главной диагонали, является базисным, (здесь он указан скобками [ ] ), а исходные номера входящих в него столбцов: _{(2) (1) (3)} -- определяют номера базисных неизвестных; остальные неизвестные – свободные, и члены уравнений, содержащие их, переносят в правую часть.

5) Полученный вид матрицы и деление неизвестных на базисные и свободные позволяют переписать систему так:

x₂ + 3x₁ -- 2x₃ = -- 3x₄ -- 5x₅

x₁ -- 3x₃ = -- 3x₄ -- 6x₅

-- 5x₃ = -- 4x₄ -- 10x₅

и выразить базисные неизвестные через свободные:

x₃ = (4/5) x₄ + 2x₅

x₁ = 3x₃ – 3x₄ – 6x₅ = (- 3/5) x₄

x₂ = -- 3x₁ + 2x₃ – 3x₄ – 5x₅ = (2/5) x₄ – x₅

6) Полученное решение представим в виде линейной комбинации столбцов фундаментальной системы решений, образующей базис в линейном пространстве решений. Таких столбцов столько, сколько свободных неизвестных (здесь = 2).Проще всего последовательно придать одной из свободных неизвестных произвольное ненулевое значение, а остальные свободные неизвестные принять нулями.

В нашем примере удобно взять

1. x₄ ⁽¹⁾ = 5, x₅ ⁽¹⁾ = 0. Тогда x₁ ⁽¹⁾ = - 3, x₂ ⁽¹⁾ = 2, x₃ ⁽¹⁾ = 4

2. x₄ ⁽²⁾ = 0, x₅ ⁽²⁾ = 1. Тогда x₁ ⁽²⁾ = 0, x₂ ⁽²⁾ = - 1, x₃ ⁽²⁾ = 2

Теперь общее решение можно записать так: x= C₁ x⁽¹⁾ + C₂ x⁽²⁾. (Здесь С₁, С₂ – произвольные постоянные), или развернуто:

[x₁] = [ - 3 ] [ 0 ]

[x₂] = [ 2 ] [ - 1 ]

[x₃] = C₁ [ 4 ] + C₂ [ 2 ]

[x₄] = [ 5 ] [ 0 ]

[x₅] = [ 0 ] [ 1 ]

Полезно проверить, что столбцы x⁽¹⁾ , x⁽²⁾ являются частными решениями исходной системы, то есть сделать прямую подстановку.

Сформулируем ответ на вопрос задачи: размерность пространства решений равна числу свободных неизвестных, (т.е. 2), а базисом в этом пространстве могут служить два найденных частных решения: x⁽¹⁾ , x⁽²⁾ .

6.Дано уравнение кривой 2-го порядка. Найти собственные значения и собственные векторы матрицы соответствующей квадратичной формы и использовать их для приведения уравнения кривой к каноническому виду. Указать тип кривой.

6.1.–x² – y² +4xy + 2x – 4y + 1 = 0 6.2. 2x² + 2y² -- 2xy -- 2x – 2y + 1 = 0

6.3.2xy + 2x – 2y = 0 6.4.-- 2x² -- 2y² +2xy -- 6x + 6y + 3 = 0

6.5.– 3x² –3y²+4xy-- 6x+ 4y+2= 0 6.6. -- 2xy -- 2x – 2y + 1 = 0

6.7. –x² – y² -- 4xy -- 4x – 2y +2= 0 6.8. --4x² -- 4y² +2xy +10x--10y +1=0

6.9. 2xy + 2x – 2y -- 1 = 0 6.10. x² + y² + 2xy -- 8x – 8y + 1 = 0

6.11. x² + y² + 4xy -- 8x – 4y +1 = 0 6.12. x² + y² -- 2xy -- 2x + 2y -- 7 = 0

6.13. 2xy + 2x + 2y -- 3 = 0 6.14. 4x² + 4y² +2xy+12x + 12y +1 = 0

6.15. 3x²+3y²+4xy +8x +12y + 1 = 0 6.16. x² + y²-- 8xy -- 20x + 20y + 1 = 0

6.17. 3x²+3y²-- 2xy--6x + 2y + 1 = 0 6.18. 4xy + 4x + 4y + 1 = 0

6.19. 3x²+3y²--4xy + 6 –4y -- 7 = 0 6.20. -- 2xy -- 2x + 2y + 3 = 0

6.21. 2x² + 2y² +4xy +8x +8y +1 =0 6.22x² + y² – 4xy +4x – 2y +1 = 0

6.233x² + 3y² – 4xy +4x +4y +1 = 0 6.24-4xy + 8x +8y +1 = 0

Рассмотрим пример 5x² + 5y² -- 2xy + 10x – 2y + 1 = 0

1) Выпишем симметричную матрицу квадратичной формы

5x² + 5y² -- 2xy: A= [ 5 -1]

[-1 5 ]

2) Находим собственные значения:

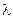Det (A – E) = 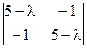= (5 – l )² – 1 = 0

Корни характеристического уравнения 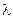² - 10 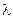+24 = 0, очевидно, таковы: 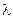₁ = 4,

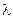₂ = 6.

3) Найдем собственные векторы матрицы А, рассматривая однородную систему:

( 5 – 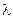)u₁ – u₂ = 0

– u₁ + ( 5 – 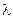)u₂ = 0

При 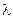₁ = 4 имеем u₁ =u₂ и в качестве первого собственного вектора примем

u⁽¹⁾ = (1 ; 1)^T .

( Знак ^(Т) означает транспонирование .) Нормируем его:

e⁽¹⁾=u⁽¹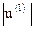⁾ / =(1 ; 1)^T / .

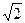(Напомним: если u = (u₁ , u₂ )^T , то | u | = .)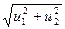

При 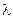₂ = 6 имеем u₁ = -u₂. В качестве второго собственного вектора примем u⁽²⁾ = (1 ; -1)^T и нормируем его:

e⁽²⁾=u⁽²⁾ / | u⁽²⁾ |=(1 ; -1)^T / .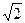

4) Сделаем замену координат 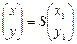, где матрица перехода S имеет столбцами нормированные собственные векторы e⁽¹⁾ ,e⁽²⁾ , то есть .

.

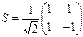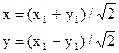В новых координатах квадратичная форма примет вид

5x² + 5y² -- 2xy = l₁x₁² + l₂ y₁² = 4x₁² + 6y₁² .

Это следует из общей теории, но полезно использовать равенство

(Ax,x) = (ASx₁, Sx₁) = ( S ^TASx₁, x₁) = ( A ₁x₁, x₁), откуда

A₁ =S ^TAS = diag(l₁ , l₂) = ,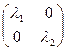

и проверить результат непосредственным матричным умножением.

В новых координатах уравнение кривой примет вид:

4x₁² + 6y₁² + 5 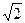(x ₁+ y ₁) -- 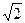(x ₁ -- y ₁) +1 = 0.

7) Параллельным переносом осей координат устраним линейные члены. Соберем члены, содержащие x ₁ и выделим полный квадрат:
4x₁ ² + 4 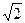x₁ = 4(x₁ + 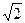/2)² – 2.

Аналогично поcтупим с членами, содержащими y₁:
6 y₁ ² + 6 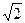y₁ =6(y₁ + 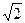/2)² – 3.

Делаем замену переменных:

x₂ = x₁ + 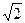/2; y₂ = y₁ + 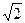/2 ,

в результате которой уравнение кривой принимает вид 4x₂ ² + 6y₂ ² – 4 = 0, и после деления на свободный член получаем

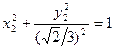-- каноническое уравнение эллипса.

Раздел 2