Алгоритм вычисления обратной матрицы
Лабораторное занятие № 3
Темы: Отыскание обратной матрицы. Матричный метод решения систем линейных уравнений(2 часа)
Учебно-познавательные цели занятия:
ознакомить студентов с алгоритмом отыскания обратной матрицы и с методикой решения систем линейных уравнений матричным методом
Воспитательные цели: Развивать алгоритмическую культуру студентов, повышать интерес к предмету в процессе решения задач
Развивающаяцель – развитие творческих способностей студентов.
На лабораторном занятии формируются понятия:
-решения системы линейных уравнений:
- совместной, несовместной, определенной и неопределенной систем;
- обратной матрицы;
- матричного уравнения.
На занятии формируются знания:
-алгоритма нахождения обратной матрицы;
- матричного метода решения систем;
умения:
- находить обратную матрицу для данной невырожденной;
- решать системы линейных уравнений матричным методом;
- решать матричные уравнения.
навыки:
- аргументированного письменного изложения собственной точки зрения;
- критического восприятия информации
компетенции:
- ОК-1–владение культурой мышления, способностью к восприятию, обобщению и анализу информации, постановке цели и выбору путей ее достижения;
- ОК-2–умением логически верно, аргументированно и ясно строить устную и письменную речь;
- ОК-11–способностью представить современную картину мира на основе естественнонаучных, математических знаний, ориентироваться в ценностях бытия, жизни, культуры;
- ПК-1 - способностью использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования;
- ПК-25 - способностью к обобщению и статистической обработкеМатериально-техническое оборудование:
мультимедийный проектор, ноутбук, «Решение систем линейных уравнений матричным методом».
ПЛАН ЗАНЯТИЯ
1. Инструктаж по ТБ.
2.Проверка знаний студентов — их теоретической готовности к выполнению заданий по каждой из следующих тем:
Алгоритм нахождения обратной матрицы
Решение систем линейных уравнений методом обратной матрицы
3. Общее описание задания.
4. Выполнение заданий.
5. Оформление отчета о лабораторной работе.
6. Анализ
Глоссарий
Выучите определения следующих терминов:
обратная матрица, нахождение обратной матрицы, решения систем линейных уравнений матричным способом
Алгоритм вычисления обратной матрицы
Вычислить определитель данной матрицы  |
| |A|¹0 |
| |A|=0 |
| Обратной матрицы нет |
| Найти транспонированную матрицу A¢ |
Найти алгебраические дополнения 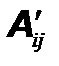 элементов матрицы A¢ и составить из них присоединенную матрицу элементов матрицы A¢ и составить из них присоединенную матрицу 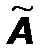 , записывая алгебраические дополнения на соответствующих местах. , записывая алгебраические дополнения на соответствующих местах. |
Найти обратную матрицу по формуле: 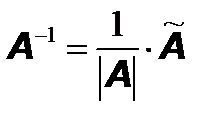 . . |
ХОД ЗАНЯТИЯ
1. Инструктаж по ТБ в компьютерном классе.
2. На лабораторном занятии используется работа в парах (или малых группах).
Студентам необходимо:
- ознакомиться с основными теоретическими сведениями по каждой
из рассматриваемых тем;
- ответить на контрольные вопросы по по каждой
из рассматриваемых тем;
- изучить решение общих исходных практических заданий;
- выполнить представленные индивидуальные задания;
- оформить отчет о лабораторной работе;
- защитить лабораторную работу
Необходимый для повторения теоретический материал по теме:
"Решение систем линейных уравнений матричным методом "
Обратная матрица.Квадратная матрица, определитель Δкоторой не равен нулю, называется невырожденной, или несобственной, матрицей, а матрица с Δ=0 называется вырожденной, или особенной, матрицей.
Матрица А-1 называется обратной для квадратной матрицы А·n-го порядка, если А· А-1= А-1· А=E.
Если определитель Δ матрицы А не равен нулю, то матрица А-1 существует, причем единственная:
А-1 = 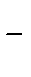
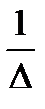
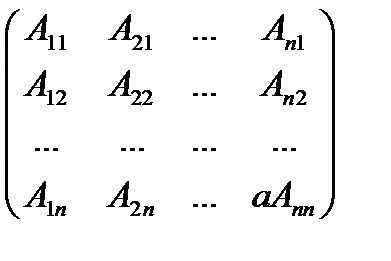 (1), где Аij—алгебраические дополнения элементов матрицы А.
(1), где Аij—алгебраические дополнения элементов матрицы А.
В сокращенной форме (1): А-1 = 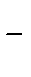
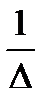 ·Ã, где Δ — определитель матрицы А, × матрица, присоединенная (транспонируемая матрица алгебраических дополнений матрицы А) к матрице А.
·Ã, где Δ — определитель матрицы А, × матрица, присоединенная (транспонируемая матрица алгебраических дополнений матрицы А) к матрице А.
Свойства обратной матрицы:
1) ( А-1)-1= А;
2) (А·В)-1= В-1 · А-1;
3) ( АТ)-1 = ( А-1)Т.
