Вычисление длины дуги плоской кривой

Прямоугольные координаты

Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у' = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).

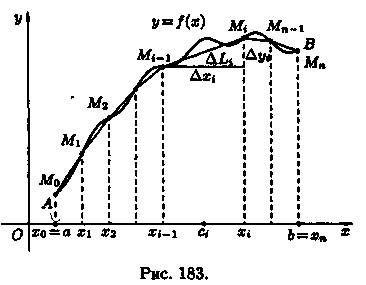
1. Точками х0 = а, х1..., хn = b (х0 < x1 < ...< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,...,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,..., Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,..., ΔLn. Получим ломаную M0M1M2 ... Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+...+ ΔLn =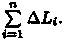

2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:

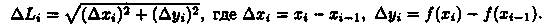
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому

а длина всей ломаной M0M1... Мn равна

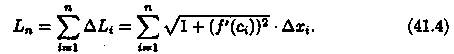
3.Длина l кривой АВ, по определению, равна

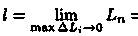
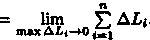
. Заметим, что при ΔLi→0 также и Δxi →0 ΔLi = 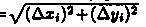и, следовательно, |Δxi|<ΔLi).

Функция 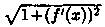непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:

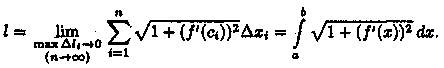
Таким образом, 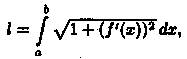или в сокращенной записи l =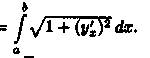

Если уравнение кривой АВ задано в параметрической форме

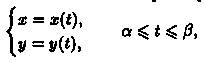
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле

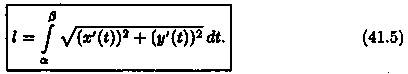
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,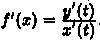

Пример 41.4. Найти длину окружности радиуса R.

Решение: Найдем 1/4 часть ее длины от точки (0;R) до точки (R;0) (см. рис. 184). Так как 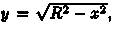то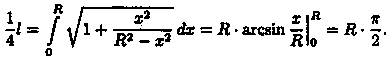

Значит, l = 2πR. Если уравнение окружности записать в параметрическом виде х=Rcost, у = Rsint (0≤t≤2π), то

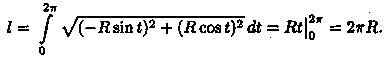
Вычисление длины дуги может быть основано на применении метода дифференциала. Покажем, как можно получить формулу (41.3), применив схему II (метод дифференциала).

1. Возьмем произвольное значение х є [а; b] и рассмотрим переменный отрезок [а;х]. На нем величина l становится функцией от х, т.е. l = l(х) (l(а) = 0 и l(b) = l).

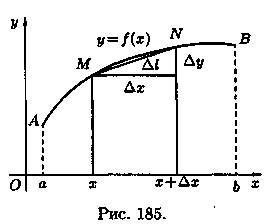
2. Находим дифференциал dl функции l = l(х) при изменении х на малую величину Δх = dx: dl = l'(x)dx. Найдем l'(x), заменяя бесконечно малую дугу MN хордой Δl, стягивающей эту дугу(см. рис. 185):

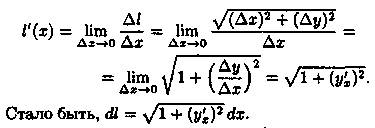
3. Интегрируя dl в пределах от а до b, получаем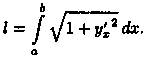

Равенство 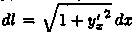называется формулой дифференциала дуги в прямоугольных координатах.

Так как у'х = -dy/dx, то

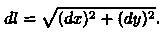
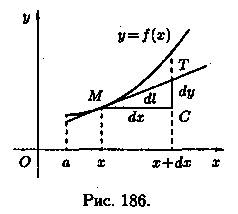
Последняя формула представляет собой теорему Пифагора для бесконечно малого треугольника МСТ (см. рис. 186).

Полярные координаты

Пусть кривая АВ задана уравнением в полярных координатах r = r(φ), а≤φ≤β. Предположим, что r(φ) и r'(φ) непрерывны на отрезке [а;β].

Если в равенствах х = rcosφ, у = rsinφ, связывающих полярные и декартовы координаты, параметром считать угол φ, то кривую АВ можно задать параметрически

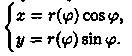
Тогда

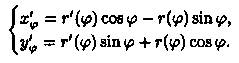
Поэтому

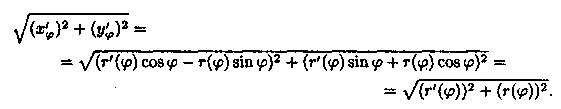
Применяя формулу (41.5), получаем

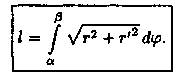
Пример 41.5. Найти длину кардиоиды r = = а(1 + cosφ).

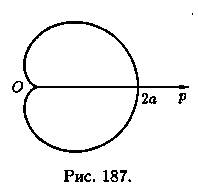Решение: Кардиоида r = а(1 + cosφ) имеет вид, изображенный на рисунке 187. Она симметрична относительно полярной оси. Найдем половину длины кардиоиды:

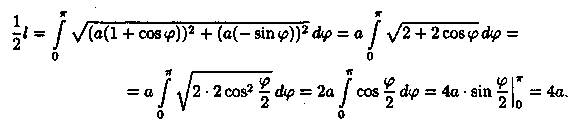
Таким образом, 1/2l= 4а. Значит, l= 8а.