Оценка эффективности многоканальной СМО
Рассмотрим многоканальную СМО,в которой выполняются следующие требования.
· На вход системы поступает простейший поток заявок;
· Каждый канал обслуживает одну заявку;
· Время обслуживания подчиняется показательному закону;
· Если хотя бы один канал свободен, то заявка принимается на обслуживание;
· Заявка теряется, если поступает в тот момент, когда все каналы заняты, т.е. другими словами это система с отказами.
Рассмотрим следующие критерии эффективности работы СМО:
1) вероятность отказа в обслуживании Pотк;
2) относительная пропускная способность π0;
3) абсолютная пропускная способность π.
Обозначим состояния системы соответствующими вероятностями (табл. 6):
Таблица 6
| Состояние СМО | Описание состояния | Вероятность |
| Все каналы свободны | P0(t) | |
| 1 канал занят | P1(t) | |
| . . . . . . . | . . . . . . . . | . . . . |
| N | Все каналы заняты | Pn(t)= Pотк |
Ф о р м у л а Э р л а н г а
Чтобы получить выражение для исходных критериев необходимо составить систему дифференциальных уравнений, связывающую вероятности предыдущих и последующих состояний СМО (уравнений Колмогорова) и, затем, решить эту систему.
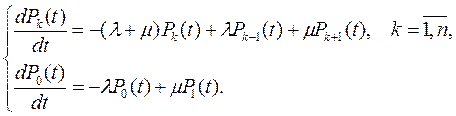
На практике часто представляет интерес установившийся процесс, описываемый стационарным решением указательной системы дифференциальных уравнений при t→∞.
При этом, для всех индексов k, от 1 до n производные равны нулю и система дифференциальных уравнений превращается в систему алгебраических уравнений Колмогорова:
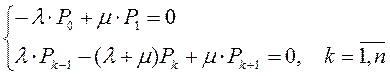
Решением подобной системы уравнений для случая n обслуживающих аппаратов является формула Эрланга, выражающая предельные вероятности состояний Pk:
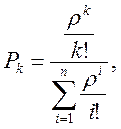
где ρ – нормированная интенсивность входного потока заявок (загрузка обслуживающего прибора).
Формула Эрланга дает вероятность того, что k каналов из n заняты обслуживанием заявок.
К р и т е р и и э ф ф е к т и в н о с т и р а б о т ы м н о г о к а н а л ь н о й СМО
С помощью формулы Эрланга найдем выражения для введенных критериев.
Вероятность отказа в обслуживании– вероятность того, что в момент прихода заявки все обслуживающие приборы будут заняты (в формуле Эрланга k = n):

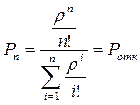
Относительная пропускная способность– вероятность обслуживания:
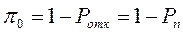

Абсолютная пропускная способность– количество заявок в единицу времени:
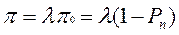

П р и м е р о ц е н к и э ф ф е к т и в н о с т и р а б о т ы
м н о г о к а н а л ь н о й СМО
Рассмотрим работу участка токарных станков.
Участок включает 3 одинаковых станка со среднем временем обработки одной детали 3 минуты.
Детали приходят на участок в среднем через 2 минуты.
Требуется определить вероятность отказа, а также относительную и абсолютную пропускную способность участка.
Решение
Три станка на участке означает, что n=3.
1. Определим среднюю скорость поступления заявок (деталей):
λ=1/2 [мин-1].
2. Определим среднюю скорость обслуживания: μ=1/3 [мин-1].
3. Найдем величину загрузки обслуживающего прибора (станка):
ρ= λ/ μ=3/2=1,5.
Если бы на участке был только один станок с такой загрузкой ρ>1, то, как известно из теории, он не справился бы с таким потоком деталей, и число отказов неограниченно возрастало бы (если учитывать очередь, то она возрастала бы до бесконечности L→∞).
4. Найдем вероятность отказа в обслуживании для трех станков, используя формулу Эрланга:
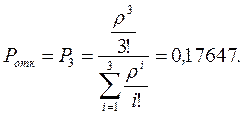

Это означает, что в среднем из 100 поступающих на обработку деталей 17 (точнее: из 1000 – 176) могут быть не приняты (отправлены назад, например, в тару), так как в это время все 3 станка заняты обработкой других деталей.
5. Найдем относительную пропускную способность (вероятность обслуживания):
π0=1 – P3= 1 – 0,17647=0,82353.
Это означает, что в среднем из 100 поступающих на участок деталей примерно 82 будут обработаны.
6. Определим абсолютную пропускную способность:
π=λ·π0=0,5·0,82353·60=24,7059[дет/час].
Заметим, что если бы детали приходили на участок не случайным образом, а регулярно, т.е. строго каждые 2 минуты, то все детали на участке успевали бы обрабатываться, и даже еще оставалось бы время, т.е. никаких отказов бы не было! Это следует из того, что среднее время обработки одной детали участком из трех станков равно:
μ3=(1/3) · 3=1[мин-1] → Т3=1/ μ3=1 [мин].
Возможности оценки характеристик СМО с использованием аналитических моделей теории массового обслуживания ограничены по сравнению с теми требованиями, которые предъявляют практические задачи, возникающие при исследовании и проектировании реальных систем.
Вопросы к разделу 5.1
- Что такое Q-схемы?
- Почему модели систем массового обслуживания относят к аналитическим?
- Почему на практике сложные модели СМО стараются не использовать?
- Что служит альтернативой использования моделей массового обслуживания?
- Для чего используются дисциплины обслуживания?
- Какой поток заявок называется простейшим?
- Какие распределения вероятностей традиционно используются для описания простейшего потока заявок?
- Почему функции многомерного распределения вероятностей Пуассона имеют экстремумы?
- Какие распределения вероятностей чаще всего используются для описания времени обслуживания?
- Какие существуют способы согласования источника заявок с обслуживающими аппаратами?
- Какими показателями характеризуется качество обслуживания?
- Какие выводы можно сделать в зависимости от величины коэффициента загрузки обслуживающего аппарата?
- Какие критерии эффективности СМО позволяет оценить формула Эрланга?
Сети Петри
Это аппарат для моделирования динамических дискретных систем (преимущественно асинхронных параллельных процессов). Сеть Петри определяется как четверка <Р,Т,I,О>, где Р и Т – конечные множества позиций и переходов, I и О – множества входных (Input) и выходных (Output) функций.
Иначе говоря, сеть Петри представляет собой двудольный ориентированный граф, в котором позициям соответствуют вершины, изображаемые кружками, а переходам – вершины, изображаемые утолщенными черточками.
Функциям I соответствуют дуги, направленные от позиций к переходам, а функциям О – от переходов к позициям.
Как и в системах массового обслуживания, в сетях Петри вводятся объекты двух типов: динамические – изображаются метками (маркерами) внутри позиций и статические – им соответствуют вершины сети Петри.
Модели в виде сетей Петри также называют N-схемами (от англ. net – сеть).

Рис. 5.12. Фрагмент сети Петри и основные понятия
Маркировка
Распределение маркеров по позициям называют маркировкой. Маркеры могут перемещаться в сети. Каждое изменение маркировки называют событием, причем каждое событие связано с определенным переходом. Считается, что события происходят мгновенно и разновременно при выполнении некоторых условий.
Каждому условию в сети Петри соответствует определенная позиция. Совершению события соответствует срабатывание (возбуждение или запуск) перехода, при котором маркеры из входных позиций этого перехода перемещаются в выходные позиции. Последовательность событий образует моделируемый процесс.
