Критерий устойчивости Михайлова

Система устойчива, если годограф характеристического вектора (кривая Михайлова), начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении (против часовой

стрелки) n квадрантов, где n - порядок характеристического уравнения системы. На рис.5.8 приведены примеры годографов для устойчивой и неустойчивойсистем.

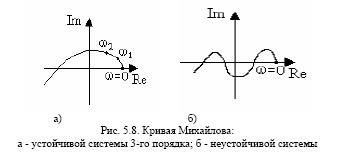
Если годограф проходит через начало координат, то система находится на границе устойчивости. В этом случае

X(ω) = 0 и Y(ω) = 0. (5.12)

А(р)=а₀рⁿ+ а₁р^n-1+….+ а_n=0 – характеристическое уравнение. р→j ω и строится гадограф Михайлова.

ВОПРОС№7

Критерий устойчивости Гурвица.

Линейная система, характеристический полином которой равен

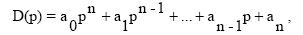
где a0>0, устойчива, если положительны n главных определителей матрицы

Гурвица:

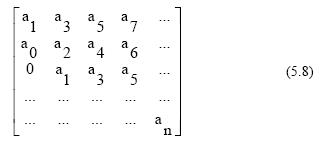
Порядок составления матрицы Гурвица следующий. На главной диагонали записываются все коэффициенты, начиная с первого. Далее заполняются строки: четными коэффициентами по порядку, если на главной диагонали стоит четный коэффициент, и нечетными, если на главной диагонали стоит нечетный коэффициент. Если какой-либо коэффициент отсутствует, то вместо него заносится нуль.

Для оценки устойчивости системы необходимо вычислить определители Гурвица

∆i (i = 1, 2, ... , n), которые получают из матрицы (5.8) путем отчеркивания равного числа строк и столбцов в левом верхнем углу матрицы. Система устойчива, если ∆i > 0 для всех i = 1, 2, ... , n.

Последний определитель Гурвица, как видно из приведенной выше матрицы, равен ∆n = an × ∆n-1. Поэтому его положительность сводится при ∆n-1>0 к условию an>0, Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов ai. Если определитель ∆n=0, то система находится на границе устойчивости. Возможны два случая: апериодическая граница устойчивости, если свободный член

характеристического уравнения равен нулю, что соответствует нейтрально устойчивой системе; колебательная граница устойчивости, если определитель ∆n-1=0. Из условия ∆n-1=0 можно определить параметры, при которых система находится на границе устойчивости.

Пример. Имеем три последовательно соединенных инерционных звена. Передаточная функция разомкнутой системы будет определена произведением трех отдельных передаточных функций:

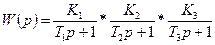
. Исследовать устойчивость системы.

Р е ш е н и е . Характеристическое уравнение замкнутой системы

D(p)=0, где D(p) =1+W(s) s = p .

Откуда следует

(T₁p+1)(T₂ p+1)(T₃ p+1)+ k = 0

.

Раскрыв скобки, получим

T₁T₂ T₃p³ + (T₁T₂+ T₂ T₃+ T₁ T₃)p² + (T₁+T₂ +T₃)p + k+1 = 0.

Тогда имеем: a0 = T₁T₂ T₃; a1 = (T₁T₂+ T₂ T₃+ T₁ T₃); a2 = (T₁+T₂ +T₃); a3 = k+1.

Коэффициенты характеристического уравнения положительны.

Составляем матрицу Гурвица

и найдем определители этой матрицы. Для устойчивости системы все они

должны быть положительными:

∆1 = a1, откуда (T₁T₂+ T₂ T₃+ T₁ T₃) > 0;

∆2 = a1×a2 − a0 ×a3, откуда (T₁T₂+ T₂ T₃+ T₁ T₃)* (T₁+T₂ +T₃)− (k+1) T₁T₂ T₃ > 0;

∆3 = a1×a2×a3 − a0×a3×a3 = a3( a1×a2 − a0×a3 ), откуда a3 >0 , то есть k+1 > 0.

ВОПРОС№8

Построение ЛАЧХ разомкнутой системы регулирования методом асимптот.

ВОПРОС№9

Характеристика показателя колебательности замкнутой системы регулирования.

ВОПРОС№10

Синтез следящей системы с астатизмом 1-го порядка.

ВОПРОС№11

Синтез следящей системы с астатизмом 2-го порядка.

ВОПРОС№12

Синтез статической системы автоматического регулирования.

ВОПРОС№13

Реализация передаточных функций регуляторов УБСР на базе ОУ постоянного тока.

ВОПРОС№14

Типовые нелинейности САУ.

ВОПРОС№15

Понятия фазового пространства и фазовой плоскости для нелинейных систем.

ВОПРОС№16

Общая характеристика метода гармонической линеаризации.

ВОПРОС№17

Комплексные коэффициенты усиления нелинейного звена.