Введение в теорию множеств
Раздел 14. Дискретная математика
1. Введение
2. Введение в теорию множеств
2.1. Основные определения
Сравнение множеств.
2.3.Операции над множествами
3. Основы математической логики
Основные понятия логики высказываний
Составные высказывания
3.3 Основные логические операции. Формулы логики.
3.4 Совершенная дизъюнктивная и конъюнктивная нормальные формы (СДНФ и СКНФ).
4. Основы теории графов
4.1 Понятие графа. Способы задания графа. Методика выделения компонента связности в графе
4.2 Изоморфные графы. Эйлеровы графы.
4.3 Плоские графы. Деревья и их свойства
4.4. Понятие ориентированного графа
4.5. Связный орграф. Эйлеровы орграфы
Введение
Понятие «дискретный» (от лат. discretus – разделенный, прерывный) является противоположным понятию «непрерывный». С содержательной точки зрения дискретный объект представляет собой нечто, состоящее из строго ограниченных, отделенных друг от друга неделимых частей.
Дискретная математика (или дискретный анализ) – совокупность математических дисциплин, изучающих свойства абстрактных дискретных объектов, которые возникают в математике и в ее приложениях. Эти объекты могут носить как конечный характер, так и бесконечный – в случае отделимости составляющих их элементов или скачкообразности происходящих в них процессов.
Деление математики на дискретную и классическую (непрерывную) математику достаточно условно. Так, например, методы теории множеств используются при изучении и дискретных, и непрерывных объектов. Дискретная математика также использует методы, разработанные в классической математике.
Однако характер исследуемых дискретной математикой объектов настолько своеобразен, что методов классической математики не всегда достаточно для их изучения. Важными отличиями дисциплин дискретной математики от классических разделов непрерывной математики являются отсутствие понятия непрерывности и предела последовательности.
В настоящее время методы дискретной математики находят широкое применение в различных областях знаний, наиболее значимой из которых является область компьютерных технологий.
К разделам дискретной математики обычно относятся: теория множеств, комбинаторика, общая алгебра, теория графов, математическая логика, теория алгоритмов, теория кодирования, теория автоматов и многие другие.
Дискретная математика знакомит с современными средствами моделирования – универсальными моделями и методами формализованного описания (представления) систем, процессов, явлений. В процессе моделирования этот класс методов занимает одно из ключевых мест. Отметим два важных обстоятельства, касающихся моделирования как процесса
- Процесс моделирования заключается в уточнении (формализации) исследуемой ситуации, системы, процесса при использовании каких-либо средств фиксации (представления) имеющихся и выявленных знаний в виде модели как результата такой формализации. Модель как описательное уточнение фиксирует то, что известно на данный момент и может быть использовано для решения проблемы. При этом к модели не будем предъявлять жестких требований обязательной представимости ее средствами классической (функциональной, вероятностной) математики. Такое представление не всегда необходимо и возможно, например, в силу сложности исследуемого объекта, различия целей исследования, степени «точности» имеющихся знаний и пр.
- При исследовании сложных систем, происходящих в них процессов, сложных управленческих ситуаций и проблем, как правило, не удается сразу представить их в виде, пригодном для принятия решений. В таких случаях моделирование становится многошаговым процессом уточнения – постепенной формализации представлений об исследуемом объекте. Так на начальных стадиях формализации моделью может являться вербальное (словесное) описание интересующего объекта. Естественный язык позволяет уточнить и описать мысленные представления. Другие методы, включающие искусственные языки (такие, как теоретико-множественные, графические, логические представления) позволяют уточнить словесное описание и т.п. в этом смысле точные методы классической математики находятся на противоположном «полюсе» по отношению к вербальному описанию. Они в наибольшей степени удовлетворяют требованиям однозначности т компактности описания.
Однако модель – это не любое описание. К обязательным относятся требования:
- прагматической значимости – модель должна фиксировать имеющиеся знания, не обязательно все (это во многих случаях просто недостижимо), но существенные для решения проблемы
- конструктивности – модель должна представлять эти знания в виде, удобном для использования в последующем процессе анализа и принятия решений, т.е. требование быть своего рода инструментом принятия решений.
В процессе моделирования используются разнообразные методы постепенной формализации, направленные на построение моделей, облегчающих решение проблемы. К ним относятся:
- методы извлечений знаний о данной предметной (проблемной) области. Такие знания могут быть отражены в различных печатных, визуальных и других источниках (книгах, отчетах, рекламных проспектах, электронных носителях информации и пр.). важными знаниями могут обладать специалисты в данной предметной (проблемной) области. Это могут быть, например, знания о законах, закономерностях, теориях существования, поведения, развития интересующего объекта, интуитивные догадки и т.п.).проблемы извлечения такого рода знаний специалистов, представления их в виде словесных описаний (вербализации знаний) или иных моделей формализованного представления изучаются в таких сравнительно новых дисциплинах, как когнитология (наука о знаниях), когнитивная психология и др.
- методы системного анализа, способствующие переходу от реального объекта к модели и обеспечивающие эффективное использование имеющихся знаний об исследуемой предметной (проблемной) области, их пополнение, уточнение и приобретение новых знаний и пр. это методы конструктивного анализа проблемных ситуаций; методы, направленные на активизацию творчества, интуиции, использование опыта в решении проблем; методы, обеспечивающие конструктивное взаимодействие и взаимопонимание между участниками, заинтересованными в решении проблемы и др. эта группа методов столь обширна и важна, что требует специального обсуждения.
- методы формализованного представления имеющихся и выявляемых знаний об исследуемом объекте в виде модели. Как методы моделирования они включают не только средства (язык) символьного (знакового) описания для построения модели, но и разработанный аппарат корректных преобразований (операций над этими символами). Такие преобразования, допустимые в данном методе, позволяют получить новые знания об объекте исследования или выявить направления, в которых могут быть получены недостающие знания, дают возможность проводить последующий анализ и формализацию.
Разумеется, такое выделение групп методов достаточно условно. Так, например, методы извлечения знаний (методы первой группы) должны включать элементы активизации интуиции и опыта, обеспечивать конструктивное взаимодействие и др. (т.е. содержать элементы методов второй группы); результатом извлечения знаний (методы первой группы) должно быть их изложение на некотором языке представления знаний (т.е. содержать элементы методов третьей группы) и т.д. очевидна также связь методов второй и третьей групп. Однако в целом следует согласиться с тем, что выделенные три группы методов обеспечивают решение разных задач в общем процессе моделирования.
Введение в теорию множеств
Теоретико-множественные представления – описание исследуемой системы, процессов средствами теории множеств, т.е. как множества взаимосвязанных и/или взаимодействующих частей – элементов. Связи между элементами задаются через отношения и/или соответствия. Множества, элементы, отношения, соответствия характеризуются определенными свойствами и набором допустимых операций над ними.
Множества
Основные определения
Наиболее простая структура данных, используемых в математике, имеет место в случае, когда между отдельными данными присутствуют какие- либо взаимосвязи. Совокупность таких данных представляет собой множество.
Понятие множество принадлежит к числу фундаментальных неопределяемых понятий математики.
Множество можно представить себе как совокупность объектов, обладающих общим свойством. Объекты, из которых составлено множество, называются его элементами.
Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись условия:
q должно существовать правило, позволяющее определить, принадлежит ли некоторый элемент множеству;
q должно существовать правило, позволяющее отличать элементы друг от друга (множество не может содержать двух одинаковых элементов).
Множества обычно обозначают большими латинскими буквами (например, A, S, D), а их элементы - строчными (например, a, s, d).
Если элемент х принадлежит множеству А, то это обозначается: х 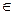 А; в противном случае говорят, что элемент не принадлежит множеству, это обозначается: х
А; в противном случае говорят, что элемент не принадлежит множеству, это обозначается: х 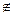 А.
А.
Примеры множеств.
1. Множество N - множество натуральных чисел. 1 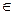 N. -1
N. -1 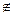 N.
N.
2. Множество L - множество букв русского алфавита. ф 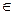 L. v
L. v 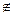 L.
L.
Множество не содержащие элементов называется пустым. Это множество обозначается 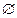 .
.
Множества можно задавать следующими способами.
4 Перечисление элементов: P={точка, прямая, плоскость, тело}, S={0,1,2}.
5 Задание характеристического свойства: L={n|n 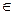 N и n<7}.
N и n<7}.
Сравнение множеств.
Множество А содержится во множестве В (множество В включает множество А, множество А является подмножеством В), если каждый элемент множества А является элементом множества В. Обозначение: А 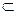 В.
В.
А 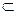 В
В 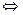 х
х 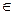 А
А 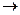 х
х 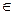 В.
В.
Два множества называются равными, если они являются подмножествами друг друга. Обозначение: А=В.
А=В 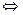 А
А 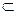 В и В
В и В 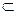 А.
А.
Если непустое множество А является подмножеством В и множества А и В не являются равными, то А является собственным подмножеством В.
Пример: М={4, 6, 8, 10}, К={6, 8}; К 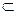 М, М
М, М 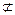 К, М
К, М 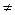 К, К – собственное подмножество М.
К, К – собственное подмножество М.
Для множеств существует понятие мощность. Для конечных множеств мощность совпадает с количеством элементов.
Пример: | 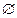 |=0, |{
|=0, |{ 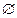 }|=1, |{1, 2, 3, 4}|=4.
}|=1, |{1, 2, 3, 4}|=4.
