Ифференциальное и интегральное исчисление.
КОНТРОЛЬНАЯ РАБОТА №1
инейная алгебра. Аналитическая геометрия. Теория пределов.
| 1 . | Дана система линейных уравнений. Требуется: 1) показать, что система совместна; 2) найти ее решение двумя способами: а) по формулам Крамера; б) методом Гаусса; 3) выполнить проверку решения. | ||||
1. 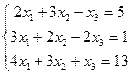 | 2. 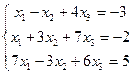 | ||||
3. 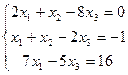 | 4. 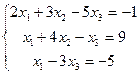 | ||||
5. 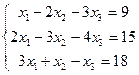 | 6. 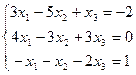 | ||||
7. 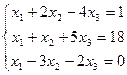 | 8. 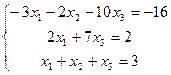 | ||||
9. 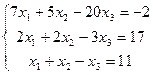 | 10. 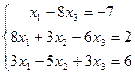 | ||||
11. 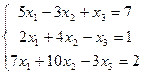 | 12. 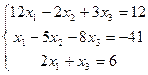 | ||||
13. 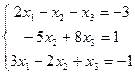 | 14. 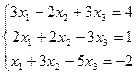 | ||||
15. 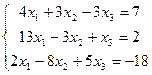 | 16. 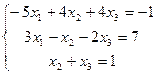 | ||||
17. 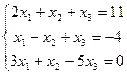 | 18. 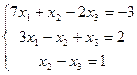 | ||||
19. 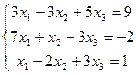 | 20. 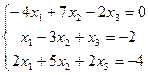 | ||||
| 2. | Методом исключения неизвестных найти общее и базисное решения систем уравнений: | ||||
1. 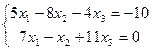 | 2. 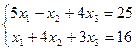 | ||||
3. 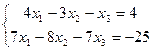 | 4. 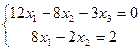 | ||||
5. 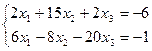 | 6. 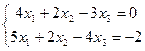 | ||||
7. 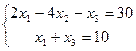 | 8. 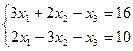 | ||||
9. 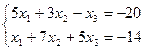 | 10. 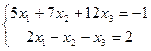 | ||||
11. 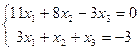 | 12. 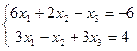 | ||||
13. 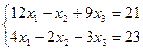 | 14. 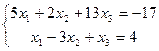 | ||||
15. 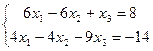 | 16. 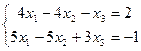 | ||||
17. 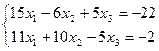 | 18. 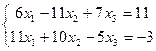 | ||||
19. 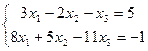 | 20. 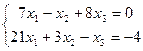 | ||||
| 3. | Даны вершины треугольника 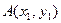 , , 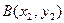 , , 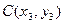 . Найти: а) уравнения всех трех его сторон; б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны; в) внутренний угол . Найти: а) уравнения всех трех его сторон; б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны; в) внутренний угол 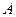 треугольника в градусах и минутах; г) длину высоты, проведенной из вершины треугольника в градусах и минутах; г) длину высоты, проведенной из вершины 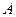 ; д) площадь треугольника. ; д) площадь треугольника. | ||||
1. 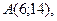
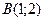 ,
, 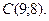
2. 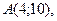
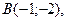 ,
, 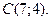
3. 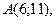
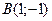 ,
, 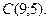
4. 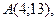
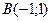 ,
, 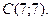
5. 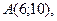
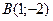 ,
, 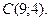
6. 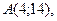
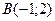 ,
, 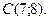
7. 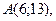
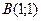 ,
, 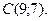
8. 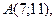
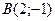 ,
, 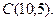
9. 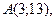
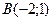 ,
, 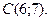
10. 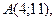
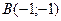 ,
, 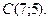
11. 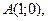
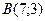 ,
, 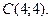
12. 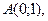
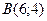 ,
, 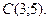
13. 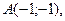
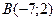 ,
, 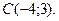
14. 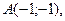
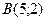 ,
, 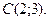
15. 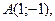
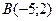 ,
, 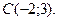
16. 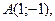
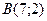 ,
, 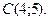
17. 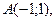
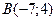 ,
, 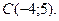
18. 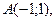
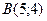 ,
, 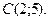
19. 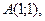
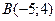 ,
, 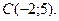
20. 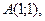
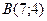 ,
, 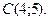
КОНТРОЛЬНАЯ РАБОТА №2
ифференциальное и интегральное исчисление.
1. Найти производные 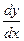 следующих функций: следующих функций: | |||||||
| 1. | а) 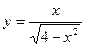 ; ; | б) 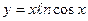 ; ; | в) 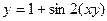 . . | ||||
| 2. | а) 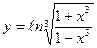 ; ; | б) 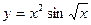 ; ; | в) 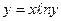 . . | ||||
| 3. | а) 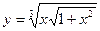 ; ; | б) 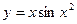 ; ; | в) 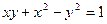 . . | ||||
| 4. | а) 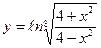 ; ; | б) 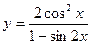 ; ; | в) 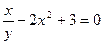 . . | ||||
| 5. | а) 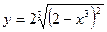 ; ; | б) 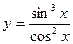 ; ; | в) 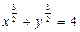 . . | ||||
| 6. | а) 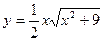 ; ; | б) 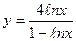 ; ; | в) 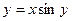 ; ; | в) 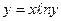 . . | |||
| 7. | а) 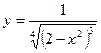 ; ; | б) 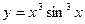 ; ; | в) 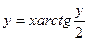 . . | ||||
| 8. | а) 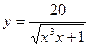 ; ; | б) 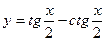 ; ; | в) 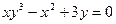 . . | ||||
| 9. | а) 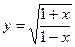 ; ; | б) 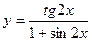 ; ; | в) 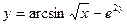 . . | ||||
| 10. | а) 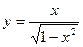 ; ; | б) 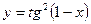 ; ; | в) 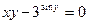 . . | ||||
| 11. | а) 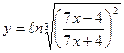 ; ; | б) 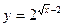 ; ; | в) 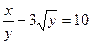 . . | ||||
| 12. | а) 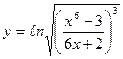 ; ; | б) 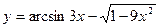 ; ; | в) 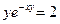 . . | ||||
| 13. | а) 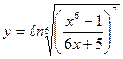 ; ; | б) 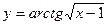 ; ; | в) 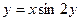 . . | ||||
| 14. | а) 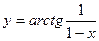 ; ; | б) 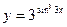 ; ; | в) 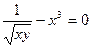 . . | ||||
| 15. | а) 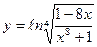 ; ; | б) 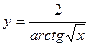 ; ; | в) 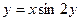 . . | ||||
| 16. | а) 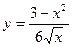 ; ; | б) 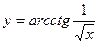 ; ; | в) 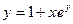 . . | ||||
| 17. | а) 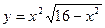 ; ; | б) 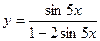 ; ; | в) 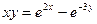 . . | ||||
| 18. | а) 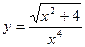 ; ; | б) 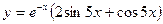 ; ; | в) 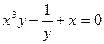 . . | ||||
| 19. | а) 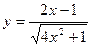 ; ; | б) 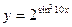 ; ; | в) 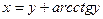 . . | ||||
| 20. | а) 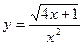 ; ; | б) 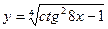 ; ; | в) 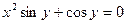 . . | ||||
| 2. | Пользуясь правилом Лопиталя найти пределы функций: | ||||
| 1. | а) 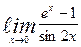 | б) 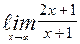 | |||
| 2. | а) 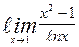 | б) 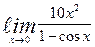 | |||
| 3. | а) 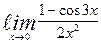 | б) 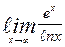 | |||
| 4. | а) 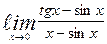 | б) 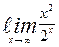 | |||
| 5. | а) 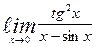 | б) 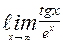 | |||
| 6. | а) 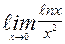 | б) 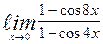 | |||
| 7. | а) 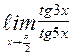 | б) 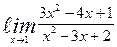 | |||
| 8. | а) 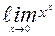 | б) 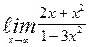 | |||
| 9. | а) 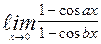 | б) 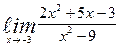 | |||
| 10. | а) 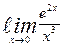 | б) 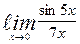 | |||
| 11. | а) 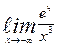 | б) 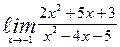 | |||
| 12. | а) 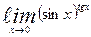 | б) 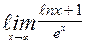 | |||
| 13. | а) 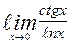 | б) 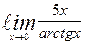 | |||
| 14. | а) 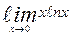 | б) 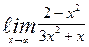 | |||
| 15. | а) 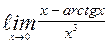 | б) 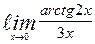 | |||
| 16. | а) 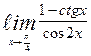 | б) 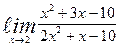 | |||
| 17. | а) 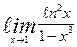 | б) 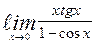 | |||
| 18. | а) 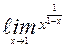 | б) 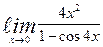 | |||
| 19. | а) 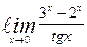 | б) 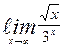 | |||
| 20. | а) 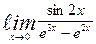 | б) 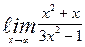 | |||
| 3. | Исследовать функцию и построить ее график | ||||
1. 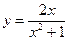 ; ; | 2. 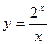 ; ; | 3. 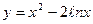 . . | |||
4. 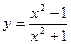 ; ; | 5. 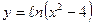 ; ; | 6. 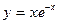 . . | |||
7. 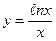 ; ; | 8. 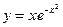 ; ; | 9. 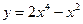 . . | |||
10. 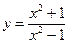 ; ; | 11. 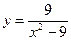 ; ; | 12. 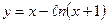 . . | |||
13. 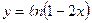 ; ; | 14. 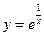 ; ; | 15. 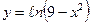 . . | |||
16. 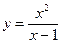 ; ; | 17. 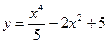 ; ; | 18. 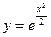 . . | |||
19. 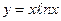 ; ; | 20. 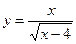 . . | ||||
| 4. | Найти частные производные и полный дифференциал функции 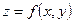 | |
1. 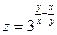 . . | 2. 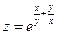 . . | |
3. 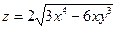 . . | 4. 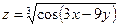 . . | |
5. 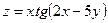 . . | 6. 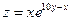 . . | |
7. 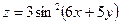 . . | 8. 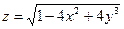 . . | |
9. 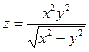 . . | 10. 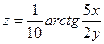 . . | |
11. 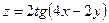 . . | 12. 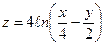 . . | |
13. 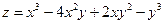 . . | 14. 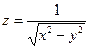 . . | |
15. 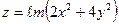 . . | 16. 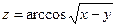 . . | |
17. 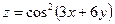 . . | 18. 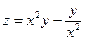 . . | |
19. 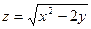 . . | 20. 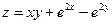 . . | |
| 5. Найти неопределенные интегралы | |||
| 1. | а) 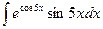 ; ; | б) 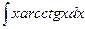 ; ; | в) 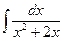 . . |
| 2. | а) 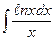 ; ; | б) 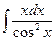 ; ; | в) 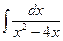 . . |
| 3. | а) 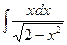 ; ; | б) 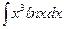 ; ; | в) 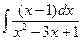 . . |
| 4. | а) 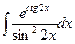 ; ; | б) 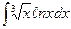 ; ; | в) 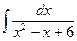 . . |
| 5. | а) 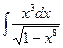 ; ; | б) 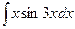 ; ; | в) 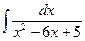 . . |
| 6. | а) 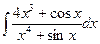 ; ; | б) 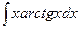 ; ; | в) 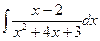 . . |
| 7. | а) 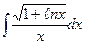 ; ; | б) 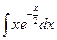 ; ; | в) 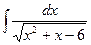 . . |
| 8. | а) 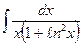 ; ; | б) 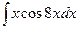 ; ; | в) 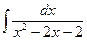 . . |
| 9. | а) 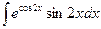 ; ; | б) 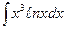 ; ; | в) 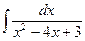 . . |
| 10. | а) 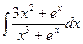 ; ; | б) 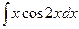 ; ; | в) 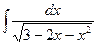 . . |
| 11. | а) 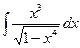 ; ; | б) 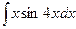 ; ; | в) 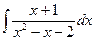 . . |
| 12. | а) 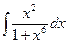 ; ; | б) 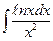 ; ; | в) 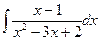 . . |
| 13. | а) 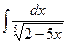 ; ; | б) 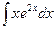 ; ; | в) 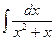 . . |
| 14. | а) 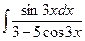 ; ; | б) 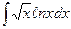 ; ; | в) 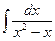 . . |
| 15. | а) 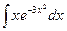 ; ; | б) 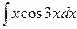 ; ; | в) 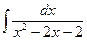 . . |
| 16. | а) 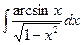 ; ; | б) 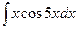 ; ; | в) 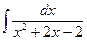 . . |
| 17. | а) 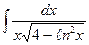 ; ; | б) 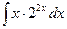 ; ; | в) 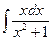 . . |
| 18. | а) 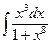 ; ; | б) 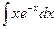 ; ; | в) 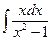 . . |
| 19. | а) 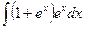 ; ; | б) 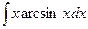 ; ; | в) 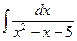 . . |
| 20. | а) 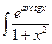 ; ; | б) 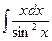 ; ; | в) 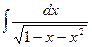 . . |
| 6. | Воспользовавшись соответствующим приложением предельного интеграла к задачам геометрии, найти следующее: | |||
| а) площадь фигуры, ограниченную линиями: | ||||
1. y = x2 , y = 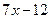 ; ; | 2. y2 = 2x + 1, x – y – 1= 0; | |||
3. y = x2 , y = 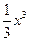 ; ; | 4. y2 = 9x , y = x + 2; | |||
5. 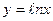 , y = 1, y = 4; , y = 1, y = 4; | 6. y = e 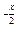 , x = 0 , x = 2 ; , x = 0 , x = 2 ; | |||
7. y = 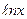 x , x = e-1, x = e; x , x = e-1, x = e; | 8. y = x2, y = 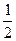 x3 ; x3 ; | |||
| 9. y = 2x , x = 0 , x = 2; | 10. y = 9 - x2, y = 0. | |||
| б) Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. | ||||
11.  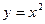 , , 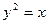 | 12. 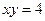 , , 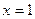 , , 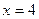 , , 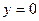 ; ; | |||
13.  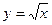 , , 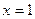 , , 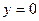 | 14. 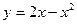 , , 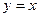 ; ; | |||
15.  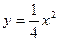 , , 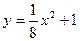 | 16. 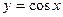 , , 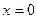 , , 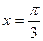 ; ; | |||
17. 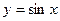 , , 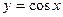 , , 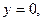 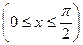 ; ; | 18. 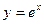 , , 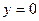 , , 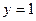 ; ; | |||
19. 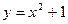 , , 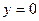 , , 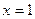 , , 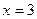 | 20. 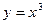 , , 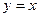 . . | |||
 Ранг матрицы
Ранг матрицы
В этом разделе рассмотрим еще одну важную числовую характиристику матрицы, связанную с тем, насколько ее строки (столбцы) зависят друг от друга.
Определение 14.10 Пусть дана матрица  размеров
размеров  и число
и число 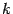 , не превосходящее наименьшего из чисел
, не превосходящее наименьшего из чисел 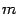 и
и 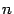 :
: 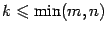 . Выберем произвольно
. Выберем произвольно 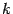 строк матрицы
строк матрицы  и
и 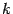 столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных
столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных 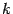 строк и
строк и 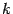 столбцов, называется минором порядка
столбцов, называется минором порядка 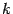 матрицы
матрицы  .
.
Пример 14.9 Пусть 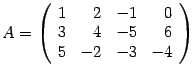 .
.
Минором первого порядка является любой элемент матрицы. Так 2, 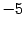 ,
, 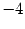 -- миноры первого порядка.
-- миноры первого порядка.
Миноры второго порядка:
1. возьмем строки 1, 2, столбцы 1, 2, получим минор 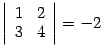 ;
;
2. возьмем строки 1, 3, столбцы 2, 4, получим минор 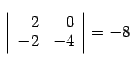 ;
;
3. возьмем строки 2, 3, столбцы 1, 4, получим минор 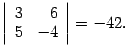
Миноры третьего порядка:
строки здесь можно выбрать только одним способом,
1. возьмем столбцы 1, 3, 4, получим минор 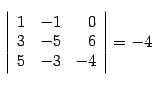 ;
;
2. возьмем столбцы 1, 2, 3, получим минор 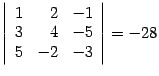 .
.
Предложение 14.23 Если все миноры матрицы  порядка
порядка 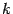 равны нулю, то все миноры порядка
равны нулю, то все миноры порядка 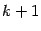 , если такие существуют, тоже равны нулю.
, если такие существуют, тоже равны нулю.
Доказательство. Возьмем произвольный минор порядка 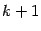 . Это определитель матрицы порядка
. Это определитель матрицы порядка 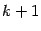 . Разложим его по первой строке. Тогда в каждом слагаемом разложения один из множителей будет являться минором порядка
. Разложим его по первой строке. Тогда в каждом слагаемом разложения один из множителей будет являться минором порядка 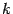 исходной матрицы. По условию миноры порядка
исходной матрицы. По условию миноры порядка 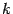 равны нулю. Поэтому и минор порядка
равны нулю. Поэтому и минор порядка 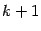 будет равен нулю.
будет равен нулю.
Определение 14.11 Рангом матрицы  называется наибольший из порядков миноров матрицы
называется наибольший из порядков миноров матрицы  , отличных от нуля. Ранг нулевой матрицы считается равным нулю.
, отличных от нуля. Ранг нулевой матрицы считается равным нулю.
Единое, стандартное, обозначение ранга матрицы отсутствует. Следуя учебнику [1], мы будем обозначать его 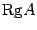 .
.
Пример 14.10 Матрица  примера 14.9 имеет ранг 3, так как есть минор третьего порядка, отличный от нуля, а миноров четвертого порядка нет.
примера 14.9 имеет ранг 3, так как есть минор третьего порядка, отличный от нуля, а миноров четвертого порядка нет.
Ранг матрицы 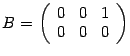 равен 1, так как есть ненулевой минор первого порядка (элемент матрицы
равен 1, так как есть ненулевой минор первого порядка (элемент матрицы 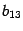 ), а все миноры второго порядка равны нулю.
), а все миноры второго порядка равны нулю.
Ранг невырожденной квадратной матрицы порядка 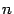 равен
равен 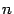 , так как ее определитель является минором порядка
, так как ее определитель является минором порядка 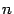 и у невырожденной матрицы отличен от нуля.
и у невырожденной матрицы отличен от нуля.
Предложение 14.24 При транспонировании матрицы ее ранг не меняется, то есть 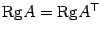 .
.
Доказательство. Транспонированный минор исходной матрицы  будет являться минором транспонированной матрицы
будет являться минором транспонированной матрицы 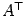 , и наоборот, любой минор
, и наоборот, любой минор 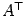 является транспонированным минором исходной матрицы
является транспонированным минором исходной матрицы  . При транспонировании определитель (минор) не меняется ( предложение 14.6). Поэтому если все миноры порядка
. При транспонировании определитель (минор) не меняется ( предложение 14.6). Поэтому если все миноры порядка 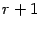 в исходной матрице равны нулю, то все миноры того же порядка в
в исходной матрице равны нулю, то все миноры того же порядка в 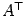 тоже равны нулю. Если же минор порядка
тоже равны нулю. Если же минор порядка  в исходной матрице отличен от нуля, то в
в исходной матрице отличен от нуля, то в 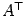 есть минор того же порядка, отличный от нуля. Следовательно,
есть минор того же порядка, отличный от нуля. Следовательно, 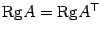 .
.
Определение 14.12 Пусть ранг матрицы равен  . Тогда любой минор порядка
. Тогда любой минор порядка  , отличный от нуля, называется базисным минором.
, отличный от нуля, называется базисным минором.
Пример 14.11 Пусть 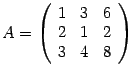 . Определитель матрицы
. Определитель матрицы  равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен
равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен 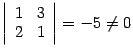 . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
. Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
Базисным минором является также минор, расположенный, скажем, в первой и третьей строках, первом и третьем столбцах: 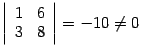 . Базисным будет минор во второй и третьей строках, первом и третьем столбцах:
. Базисным будет минор во второй и третьей строках, первом и третьем столбцах: 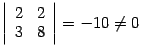 .
.
Минор в первой и второй строках, втором и третьем столбцах 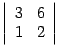 равен нулю и поэтому не будет базисным. Читатель может самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
равен нулю и поэтому не будет базисным. Читатель может самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
Так как столбцы (строки) матрицы можно складывать, умножать на числа, образовывать линейные комбинации, то можно ввести определения линейной зависимости и линейной независимости системы столбцов (строк) матрицы. Эти определения аналогичны таким же определениям 10.14, 10.15 для векторов.
Определение 14.13 Система столбцов (строк) называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что линейная комбинация столбцов (строк) с этими коэффициентами будет равна нулю.
Определение 14.14 Система столбцов (строк) является линейно независимой, если из равенства нулю линейной комбинации этих столбцов (строк) следует, что все коэффициенты этой линейной комбинации равны нулю.
Верно также следующее предложение, аналогичное предложению 10.6.
Предложение 14.25 Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы.
Сформулируем теорему, которая называется теорема о базисном миноре.
Теорема 14.2 Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор.
Доказательство можно найти в учебниках по линейной алгебре, например, в [1], [3].
Предложение 14.26 Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему.
Доказательство. Пусть ранг матрицы  равен
равен  . Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. По предложениям 14.15 и 14.18 этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно
. Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. По предложениям 14.15 и 14.18 этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно  .
.
Предположим, что 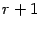 столбцов образуют линейно независимую систему. Составим из них матрицу
столбцов образуют линейно независимую систему. Составим из них матрицу 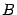 . Все миноры матрицы
. Все миноры матрицы 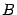 являются минорами матрицы
являются минорами матрицы  . Поэтому базисный минор матрицы
. Поэтому базисный минор матрицы 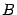 имеет порядок не больше
имеет порядок не больше  . По теореме о базисном миноре, столбец, не проходящий через базисный минор матрицы
. По теореме о базисном миноре, столбец, не проходящий через базисный минор матрицы 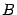 , является линейной комбинацией столбцов, проходящих через базисный минор, то есть столбцы матрицы
, является линейной комбинацией столбцов, проходящих через базисный минор, то есть столбцы матрицы 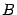 образуют линейно зависимую систему. Это противоречит выбору столбцов, образующих матрицу
образуют линейно зависимую систему. Это противоречит выбору столбцов, образующих матрицу 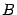 . Следовательно, максимальное число столбцов, образующих линейно независимую систему, не может быть больше
. Следовательно, максимальное число столбцов, образующих линейно независимую систему, не может быть больше  . Значит, оно равно
. Значит, оно равно  , что и утверждалось.
, что и утверждалось.
Предложение 14.27 Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему.
Доказательство. По предложению 14.24 ранг матрицы при транспонировании не меняется. Строки матрицы становятся ее столбцами. Максимальное число новых столбцов транспонированной матрицы, (бывших строк исходной) образующих линейно независимую систему, равно рангу матрицы.
Предложение 14.28 Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Доказательство. Пусть порядок матрицы  равен
равен 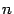 . Определитель является единственным минором квадратной матрицы, имеющим порядок
. Определитель является единственным минором квадратной матрицы, имеющим порядок 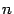 . Так как он равен нулю, то
. Так как он равен нулю, то 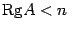 . Следовательно, система из
. Следовательно, система из 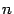 столбцов (строк) является линейно зависимой, то есть один из столбцов (одна из строк) является линейной комбинацией остальных.
столбцов (строк) является линейно зависимой, то есть один из столбцов (одна из строк) является линейной комбинацией остальных.
Результаты предложений 14.15, 14.18 и 14.28 дают следующую теорему.
Теорема 14.3 Определитель матрицы равен нулю тогда и только тогда, когда один из ее столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Определение 14.15 Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
Предложение 14.29 При элементарных преобразованиях ранг матрицы не меняется.
Доказательство. Пусть ранг матрицы  равен
равен  ,
, 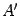 -- матрица, получившаяся в результате выполнения элементарного преобразования.
-- матрица, получившаяся в результате выполнения элементарного преобразования.
Рассмотрим перестановку строк. Пусть 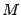 -- минор матрицы
-- минор матрицы  , тогда в матрице
, тогда в матрице 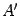 есть минор
есть минор 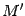 , который или совпадает с
, который или совпадает с 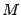 , или отличается от него перестановкой строк. И наоборот, любому минору
, или отличается от него перестановкой строк. И наоборот, любому минору 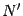 матрицы
матрицы 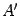 можно сопоставить минор матрицы
можно сопоставить минор матрицы  или совпадающий с
или совпадающий с 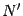 , или отличающийся от него порядком строк. Поэтому из того, что в матрице
, или отличающийся от него порядком строк. Поэтому из того, что в матрице  все миноры порядка
все миноры порядка 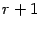 равны нулю, следует, что в матрице
равны нулю, следует, что в матрице 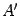 тоже все миноры этого порядка равны нулю. И так как в матрице
тоже все миноры этого порядка равны нулю. И так как в матрице  есть минор порядка
есть минор порядка  , отличный от нуля, то и в матрице
, отличный от нуля, то и в матрице 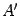 тоже есть минор порядка
тоже есть минор порядка  , отличный от нуля, то есть
, отличный от нуля, то есть 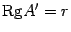 .
.
Рассмотрим умножение строки на число 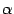 , отличное от нуля. Минору
, отличное от нуля. Минору 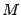 из матрицы
из матрицы  соответствует минор
соответствует минор 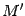 из матрицы
из матрицы 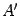 или совпадающий с
или совпадающий с 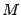 , или отличающийся от него только одной строкой, которая получается из строки минора
, или отличающийся от него только одной строкой, которая получается из строки минора 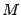 умножением на число, отличное от нуля. В последнем случае
умножением на число, отличное от нуля. В последнем случае 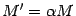 . Во всех случаях или
. Во всех случаях или 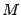 и
и 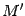 одновременно равны нулю, или одновременно отличны от нуля. Следовательно,
одновременно равны нулю, или одновременно отличны от нуля. Следовательно, 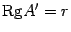 .
.
Пусть к 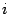 -ой строке матрицы
-ой строке матрицы  прибавлена ее
прибавлена ее 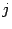 -ая строка, умноженная на число
-ая строка, умноженная на число 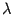 . Рассмотрим миноры порядка
. Рассмотрим миноры порядка 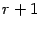 в матрице
в матрице 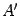 . Если через минор
. Если через минор 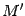 не проходит
не проходит 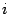 -ая строка, то он совпадает с минором
-ая строка, то он совпадает с минором 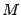 , расположенным в тех же строках и столбцах в матрице
, расположенным в тех же строках и столбцах в матрице  , и следовательно, равен нулю.
, и следовательно, равен нулю.
Если через минор 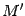 проходят и
проходят и 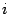 -ая и
-ая и 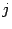 -ая строки, то он получается из минора
-ая строки, то он получается из минора 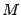 , расположенного в тех же строках и столбцах матрицы
, расположенного в тех же строках и столбцах матрицы  , прибавлением к
, прибавлением к 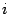 -ой строке минора
-ой строке минора 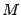
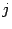 -ой строки, умноженной на
-ой строки, умноженной на 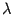 . По свойству определителя
. По свойству определителя 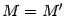 . Следовательно,
. Следовательно, 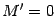 .
.
Пусть через минор 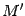 проходит
проходит 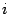 -ая строка и не проходит
-ая строка и не проходит 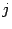 -ая. Тогда
-ая. Тогда 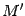 отличается от
отличается от 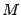
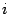 -ой строкой. Эта строка в
-ой строкой. Эта строка в 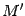 является строкой
является строкой 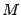 , к которой добавлены элементы
, к которой добавлены элементы 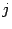 -ой строки, умноженные на
-ой строки, умноженные на 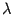 . По свойствам определителей
. По свойствам определителей 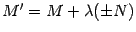 , где
, где 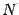 -- минор порядка
-- минор порядка 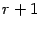 матрицы
матрицы  , стоящий в
, стоящий в 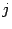 -ой строке и в тех же строках, что и минор
-ой строке и в тех же строках, что и минор 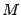 , исключая
, исключая 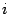 -ую, а знак "
-ую, а знак " 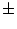 " связан с возможным изменением порядка строк. Так как все миноры порядка
" связан с возможным изменением порядка строк. Так как все миноры порядка 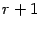 в матрице
в матрице  равны нулю, то
равны нулю, то 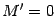 .
.
