Функция. способы задания функции.
Действительные числа и переменные.
Множество R действительных чисел состоит из двух частей : множество Q рациональных чисел и множества I иррациональных чисел.Обычно действительные числа записывают в виде десятичных дробей. Десятичная запись рационального числа ± 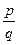 ―конечная, если знаменатель q несократимой дроби
―конечная, если знаменатель q несократимой дроби 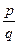
делится без остатка только на числа 1,2,5, и бесконечная периодическая – в остальных случаях; десятичная же запись
иррационального числа всегда бесконечная и притом непериодическая. Так, например: 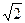 =1,4142…, π =3,14159…, lg2=0,30103… и.т.д.
=1,4142…, π =3,14159…, lg2=0,30103… и.т.д.
Принадлежать числа х множеству Х будем обозначать при помощи так называемого символа «включения»: х Є Х.
Любое число С, не меньшее всякого числа х, принадлежашего множеству Х, называется верхней границей множества Х:С≥х ,если хЄХ. Аналогично нижней границей множества Х называется любое число с, не большее всякого числа х, принадлежащего множеству с≤х , если хЄХ. Множества,  имеющие верхнюю границу, называются ограниченными сверху, имеющие нижнюю границу ограниченными снизу. Множества, ограниченные и сверху и снизу, называются просто ограниченными.
имеющие верхнюю границу, называются ограниченными сверху, имеющие нижнюю границу ограниченными снизу. Множества, ограниченные и сверху и снизу, называются просто ограниченными.
Функция. Способы задания функции.
Величина у называется функцией переменной величины х, если каждому числовому значению х, принадлежащему некоторой области его изменения Х(хЄХ) , соответствует единственное определенное числовое значение величины у . Переменную величину х называют независимой переменной, или аргументом. Область Х изменения аргумента х называется областью определения функции у, а множества числовых значений функции у, принятых его области определения Х, называется областью ее значений У .
Аналитическим способом называется способ задания функции при помощи формулы, позволяющей по каждому числовому значению аргумента х из области определения Х вычислить соответствующее ему числовое значение функции у.
Например: у=х 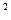 +1, у=
+1, у= 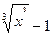 , у=3
, у=3 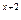 , х
, х 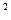 +у
+у 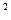 .
. 
Если зависимость между у и х задана формулой, разрешенной относительно у, т.е. имеет вид у=f(х), то соответствующая функция называется явной. Если формула не разрешена относительно функции, т.е. имеет вид 
 F(x,y)=0, то функция называется неявной. Например: 2х+у
F(x,y)=0, то функция называется неявной. Например: 2х+у 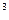 -1=0 , х
-1=0 , х 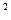 -у
-у 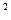 -а
-а 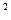 =0 и .т.д
=0 и .т.д 
Будем называть функцию у аргумента х, заданную с помощью равенств х=φ(t), у= φ(t), параметрически заданной.
Табличным способом задания называется способ задания функции с помощью таблицы, в которой ряд заранее выбранных числовых значений аргумента х, обычно расположенных в возрастающем порядке, поставлены в соответствие с числовыми значениями функции у. Графиком функции у=f(х) называется кривая, отнесенная к системе координат, точки которой имеют абсциссами значения х , относящиеся к области определения функции, а ординатами у, т.е.соответствующие этим значениям х значения функции.
3.Обратная функция.
Две функции у=f(х) и х=φ(у) называются взаимно обратными, если для каждой пары значений а,в, удовлетворяющих условию в=f(a), удовлетворяется также условие a=φ(в) ,а для каждой пары , удовлетворяющей условию a=φ(в) , удовлетворяется условие в=f(a) . Функция х=φ(у), называется обратной поотношению к функции у=f(х). Для того чтобы из функции у=f(х) получить обратную, следует в ней поменять местами аргумент и функцию. Функция у=φ[f(х)] называется сложной функцией аргумента х, функции z=f(х) и у=f(z) – простыми функциями своих аргументов, z- промежуточный аргумент.
Задание на СРС:
- Основные элементарные функции, их свойства и графики. [1,2]
- ИДЗ-4,2 [3, c. 146]
Задание на СРСП:
- Неявные, обратные и обратно - тригонометрические функции.[3]
- Вычисление значения сложной функции.[2,4]
Контрольные вопросы:
А. Для письменного контроля
1) Натуральные, целые, рациональные и иррациональные числа .
2) Множество действительных чисел.
3) Определение функции, свойства и графики.
4) Обратные и сложные функции.
Б. Для компьютерного тестирования
1. Дана 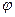 (х)=
(х)= 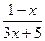 . Написать выражение:
. Написать выражение: 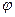 (
( 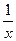 ).
).
А) 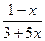 . В)
. В) 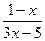 . С)
. С) 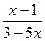 . Д)
. Д) 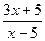 . Е)
. Е) 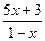 .
.
2. Найти область определения функции: у= 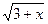 +
+ 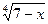 .
.
А) -3 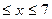
 В) х
В) х 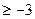 С) х
С) х 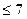 Д) -3<х<7 Е) х>-3
Д) -3<х<7 Е) х>-3
3. 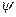 (х)=
(х)= 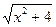 . Написать выражения:
. Написать выражения: 
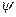 (
( 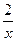 ).
).
А) 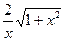 В)
В) 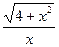 С)
С) 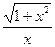 Д)
Д) 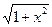 Е)
Е) 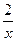
4. Найти область определения функции: у=arcsin(2x 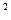 -1)
-1)
А) [0;1] B) [-1;1] C) [0;+∞) Д)[-1;0] E) [1;+∞)
Глоссарий.
| Казахский | Русский | Английский |
| Функция Нақты Өспелі Кемімелі Жұп Тақ | Функция Действительные Возрастающая Убывающая Четная Нечетная | Function Real Progressive Decrease Even Odd |
Список литературы
Основная:
1. К.Кабдыкайыр. Сборник задач по Высшей математике. Учебное пособие. Алматы: «Дәуір», 2007. -408стр.
2. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах: Учебное пособие для втузов.- М.: Оникс, 2007, 2006
3. Байбазаров М.Б., Божанов Е.Т., Уразмагамбетова Э.У .Лекционный курс по математике. Учебное пособие, часть 1. Алматы, КазГАСА, 2003.
4. Индивидуальные задания по высшей математике под общей редакцией доктора физико-математических наук проф. А.П. Рябушко. Учебное пособие. II-часть.Минск, «Высшая школа», 2002г.
Дополнительная:
5. Сыдыкова Д.К. Математика 1. Методическое руководство к выполнению заданий для СРС. Алматы: КазГАСА, 2008.
6. Кремер Н.Ш., Путко Б.А. Высшая математика для экономистов. Учебник. Изд. Объединение «ЮНИТИ»,2006. -479стр.
