Примеры выполнения курсовой работы

Пример 1. Несвободная система с двумя степенями свободы. Дано: Полый цилиндр 2 массой m₂ (рис. 6.4) скользит по основанию 1 массой m₁, способному вращаться вокруг неподвижного цилиндрического шарнира О. Основание удерживается спиральной пружиной с крутильной жесткостью C_j. В начальном положении механизм находится в состоянии статического равновесия и пружина деформирована. Введем неподвижную систему координат OXYZ так, чтобы ось OX была горизонтальна, и связанную с основанием систему координат OX₁Y₁Z₁, ее ось OX₁ параллельна оси цилиндра и направляющим основания, по которым скользит цилиндр. Центр масс основания O₁ в системе координат OX₁Y₁Z₁ имеет координаты x_1O и y_1O. Начальное положение O_н центра масс цилиндра O₂ определяется координатами x_2O и y_2O точки O_н в системе координат OX₁Y₁Z₁.

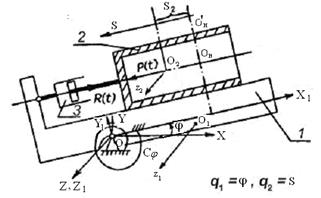
Рис. 6.4

В начальный момент времени к внутренней поверхности дна цилиндра прикладывается нагрузка 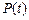, определяемая по формуле (6.1). При этом цилиндр начинает двигаться по основанию, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией тормозного устройства 3, приложенной к внешней поверхности дна цилиндра 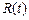, определяемой по формуле (6.2).

Коэффициент трения скольжения при движении цилиндра по основанию f = 0,12. Моменты инерции основания и цилиндра относительно осей O₁z₁ и O₂z₂ равны J₁ и J₂ соответственно. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.

Указание. В качестве обобщенных координат выбрать угол поворота j основания, отсчитанный от горизонтали (в начальный момент j = j₀), и координату S центра масс цилиндра на направляющей основания, отсчитанную от его начального положения. Исходные данные:

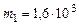кг, кг,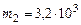

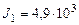кг∙м², 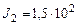кг∙м²,

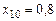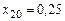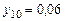м, м,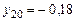

м, м,

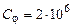Н∙м/рад , .

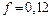Решение.Система имеет две степени свободы k = s , в качестве обобщенных координат выбираем:

1) угол поворота j основания вместе с цилиндром , отсчитанный от горизонтали (в начальный момент j = j₀), q₁=j;

2) координату S движения центра масс цилиндра 2 на направляющей основания 1, отсчитанную от его начального положения, q₂=S.

Таким образом, обобщенные координаты: q₁=j, q₂=S, обобщенные скорости: .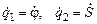

Запишем уравнения Лагранжа второго рода

.

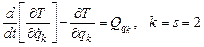Кинетическая энергия рассматриваемой механической системы относительно неподвижной системы отсчета: Т=Т₁+Т₂. Представим ее как функцию времени t, обобщенных координат q₁=j, q₂=S и обобщенных скоростей 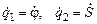, а именно:

T = T (q₁=j, q₂=S, 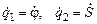, t).

Кинетическая энергия основания, совершающего вращательное движение относительно оси OZ,

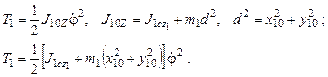
Кинетическая энергия цилиндра, совершающего плоско-параллельное движение относительно неподвижной системы отсчета,

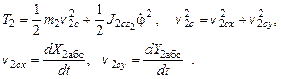
Формулы преобразования координат и поворотная матрица 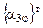относительно оси OZ в соответствии с формулами (3.18) и (3.19) имеют следующий вид:

– для центра масс основания

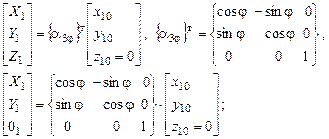
– для центра масс цилиндра

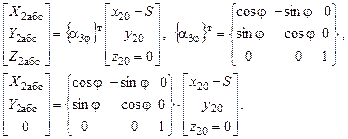
Матрица скоростей:

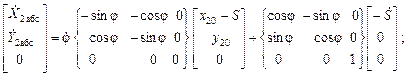
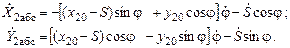
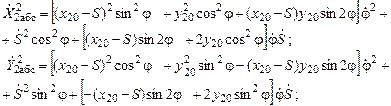
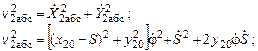
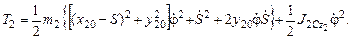
После приведения подобных членов относительно обобщенных скоростей, получаем T= T₁+T₂,

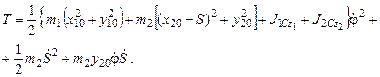
Уравнения Лагранжа второго рода для данной системы имеют следующий вид:

– для q₁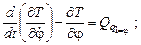

– для q₂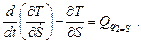

Вычислим производные от кинетической энергии системы:

– для q₁ =φ ,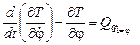

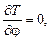
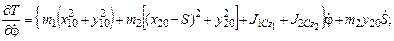
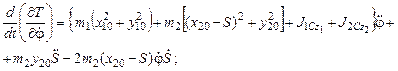
окончательно

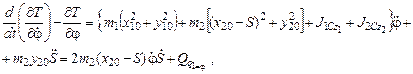где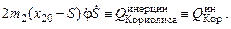

Для q₂ =S ,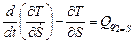

.

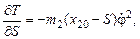
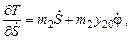
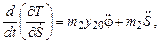
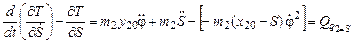В левой части уравнений Лагранжа, как правило, оставляют слагаемые со вторыми производными от обобщенных координат. Все остальные переносятся в правую часть. Таким образом, обозначив слагаемое в последнем выражении как - 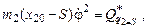окончательно получаем уравнение Лагранжа второго рода

.

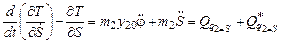Обобщенные силы для механических систем с числом степеней свободы i = s = 2 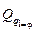, , 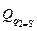отвечающие выбранным обобщенным координатам, целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации не зависят друг от друга. Системе всегда можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае из (2.15) получаем:

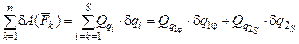. (6.6)

Для определения обобщенной силы 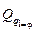дадим системе такое приращение, что 1) 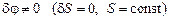, и найдем виртуальную работу от всех заданных активных сил:

,

, ,

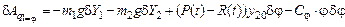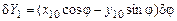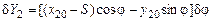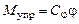
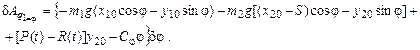
Сравнивая множитель (в квадратных скобках) в выражении виртуальной работы перед вариацией dj с формулой (6.6), получаем выражение для первой обобщенной силы

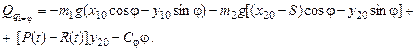Определяя 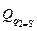, будем полагать, что dS ¹ 0,а для угла jповорота цилиндра 2, будем считать dj =0 (j =const), т.е.

2)dS ¹ 0, dj =0 (j = const); .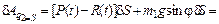

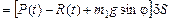Сравнивая множитель (в квадратных скобках) в выражении полученной виртуальной работы перед вариацией dS с формулой (6.6), получаем выражение для второй обобщенной силы

.

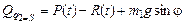Составим дифференциальные уравнения в виде матриц

.

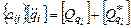Для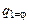

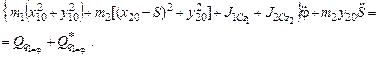
Для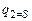

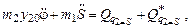
окончательно

1)

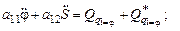
2) ,

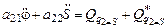где 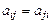, если 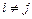, , 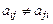если ,

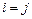т.е. ;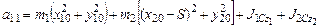

;

.

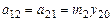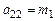Пример 2. Несвободная система с тремя степенями свободы.Дано.Рекомендуемые значения физических величин (рис. 6.5): m₁ = 3 700 кг – масса тела; 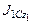= 10 300 кг·м² – момент инерции относительно оси О₁z₁; l₁ = 3,8 м – расстояние от точки С до точки К; координаты центра масс тела О₁в системе координат СX₁Y₁Z₁: х₁₀ = 3,8 м , y₁₀ = 0,8 м, y₂₀ = 1,0 м – расстояние от линии действия силы 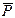до оси СХ₁ ; С₁ = 2,0·10⁶ Н/м – жесткость пружины КМ; С₂ = 2,0·10⁷ Н/м – жесткость пружины CD ; С₃ = 2,0·10⁷ Н/м – жесткость пружины СЕ; С_j = 2,0·10⁶ Нм/рад – жесткость спиральной пружины; j₀ = 6°, 30° – начальный угол возвышения основания.

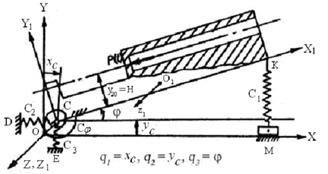
Рис. 6.5

За обобщённые координаты приняты следующие параметры:

q₁ = x_C , q₂ = y_C , q₃ = j. q₁ = x_C – перемещение шарнира С по горизонтальной оси, отсчитанное от положения статического равновесия пружины CD; q₂ = y_C – перемещение шарнира С вдоль вертикальной оси, отсчитанное от положения статического равновесия пружины CЕ; q₃ = j – угол поворота тела, отсчитанный от горизонтали СХ₁.

Кинетическая энергия рассматриваемого тела, совершающего плоскопараллельное движение относительно неподвижной системы отсчета и связанной с ней системой координат XOYZ:

.

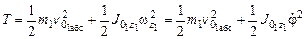Формулы преобразования координат от СX₁Y₁Z₁ к XOYZ и поворотная матрица 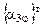относительно оси СZ в соответствии с формулами (3.18) и (3.19) для центра масс тела 1 имеют следующий вид:

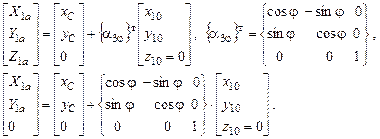
Матрица скоростей:

.

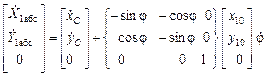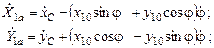
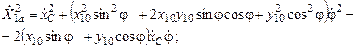
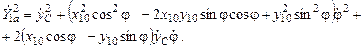
Квадрат абсолютной скорости центра масс тела в обобщённых координатах:

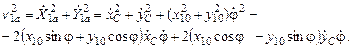
Кинетическую энергию тела представим как функцию времени t, обобщенных координат q₁ = x_C , q₂ = y_C , q₃ = j и обобщенных скоростей :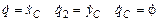

T = T (q₁=x_C, q₂ = y_C , q₃ = j, .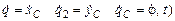

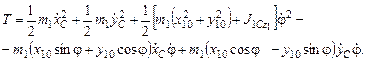
Уравнения Лагранжа второго рода для данной системы имеют вид:

– для ;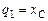

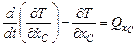– для ;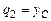

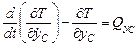– для .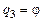

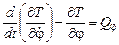Частные производные по обобщённым координатам:

;

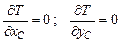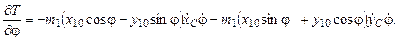
Частные производные по обобщённым скоростям:

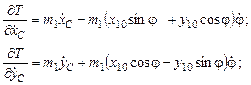
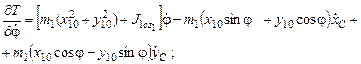
Полные производные по времени:

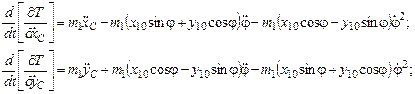
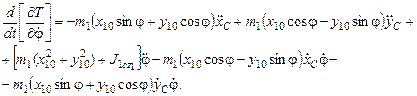
Запишем окончательно левые части уравнений Лагранжа второго рода, оставив только слагаемые со вторыми производными от обобщенных координат. Все остальные слагаемые перенесем в правую часть уравнения, обозначив их как :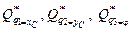

–

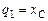
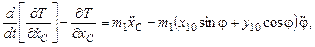
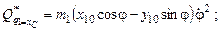
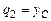
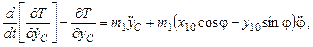
где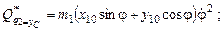

–

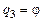
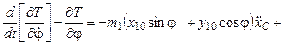
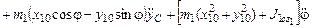где

–

, где .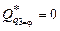

Для нахождения обобщенных сил 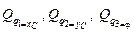рассмотрим приложенные к системе силы. Определим первоначальные сжатия пружин КМ и СЕ в положении статического равновесия.

Уравнение равенства моментов при t=0 относительно оси CZ₁

,

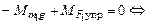
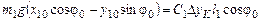где 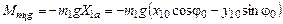- момент силы тяжести в момент времени t=0; 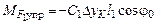– момент силы упругости пружины КМ. Отсюда

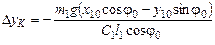- первоначальное сжатие пружины КМ.

Уравнение равенства сил по оси OY

,

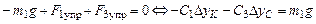где 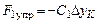– сила упругости пружины КМ; 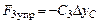– сила упругости пружины СЕ, отсюда

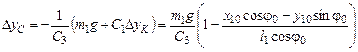- первоначальное сжатие пружины СЕ

Силы, действующие на тело в текущий момент времени t:

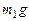– сила тяжести;

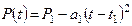– переменная нагрузка, прикладываемая к телу; где Р₁ = 2,37·10⁶ Н – максимальная нагрузка;
а₁ = 6,68·10¹⁰ Н/с² – коэффициент; t₁ = 0,005 с – временной параметр;

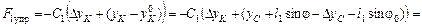
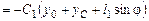– сила упругости пружины КМ,

где 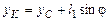– координата точки К в момент времени t ; 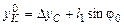– координата точки К в начальный момент времени; 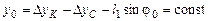– константа;

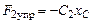– сила упругости пружины CD ; –

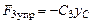сила упругости пружины СЕ.

Моменты, действующие на тело, относительно оси CZ₁ :

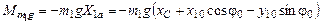– момент силы тяжести;

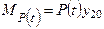– момент переменной нагрузки;

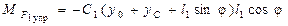– момент силы упругости пружины КМ;

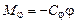– момент спиральной пружины.

Виртуальная работа согласно (2.15)

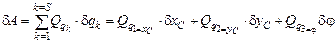. (6.7)

Так как обобщённые координаты – независимые друг от друга параметры, то и их вариации тоже независимы. Поэтому, используя принцип замораживания, находим виртуальные работы, соответствующие виртуальным перемещениям поочередно:

1) ,

;

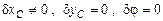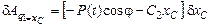2) 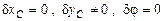, (6.8)

;

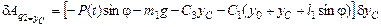3) ,

.

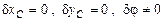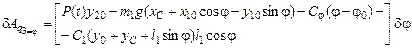Сравнивая множители в (6.7) перед вариациями обобщённых координат и в формуле (6.8), находим обобщённые силы, соответствующие обобщённым координатам:

;

;

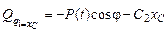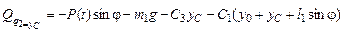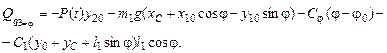
Окончательный вид уравнений Лагранжа второго рода или дифференциальные уравнения движения рассматриваемой системы в обобщенных координатах:

–

,

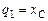
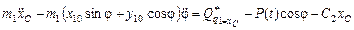где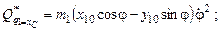

–

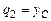
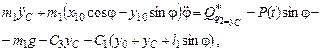
где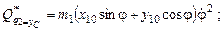

–

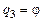
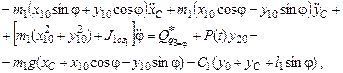
где ,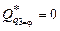

или в матричной форме ,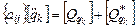

где 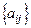– инерционная матрица, 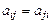, если 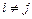, , 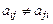если ,

,

=

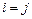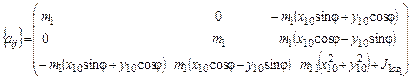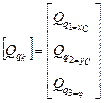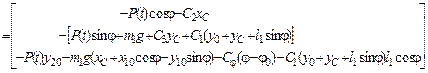– матрица-столбец обобщенных сил;

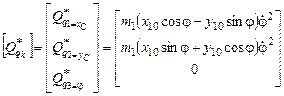– матрица-стол-бец слагаемых, перенесенных из левых частей уравнений Лагранжа, не содержащих обобщенных ускорений.

Решение системы уравнений Лагранжа второго рода, описывающих движение указанной механической системы (рис. 6.5), на интервале времени от t = 0 до t = 0,01 с выполнено в системе Mathcad 11. Распечатка результатов расчёта в системе Mathcad 11 для начального угла j₀ = 30° приведена на рис. 6.6, а для начального угла j₀ = 6° на рис. 6.7.

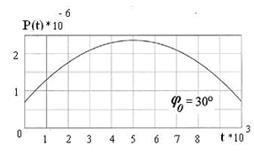
Рис. 6.6

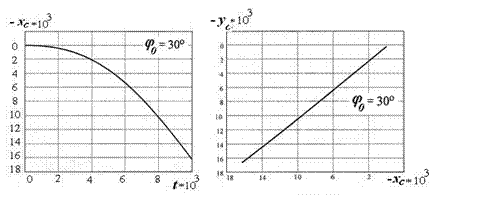
Рис. 6.6. Окончание

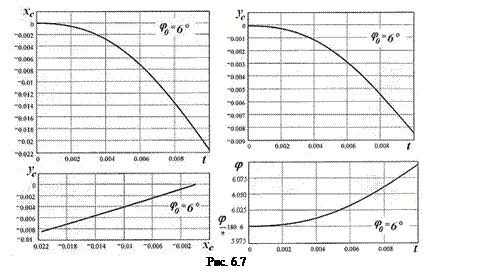
Пример 3. Несвободная система с тремя степенями свободы.Дано. Полый цилиндр 2 массой m₂ (рис. 6.8) скользит по основанию 1 массой m₁, опирающемуся на цилиндрический шарнир О и поддерживаемому вертикальной пружиной КМ. Жесткость пружины C₁, длина недеформированной пружины l₂, расстояние от шарнира О до точки К опоры пружины l₁. Коэффициент трения цилиндра об основание f = 0,12. K шарниру C прикреплена горизонтальная пружина CD жесткостью C₂. В начальном положении пружина CD не деформирована, а пружина КМ поддерживает систему в положении статического равновесия.

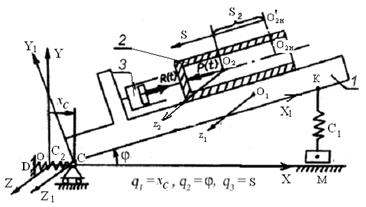
Рис.6.8

Введем неподвижную систему координат OXYZ, ось OX которой горизонтальна, и связанную с основанием систему координат OX₁Y₁Z₁, ее ось OX₁ параллельна направляющей основания, по которой скользит цилиндр. Положение центра масс O₁ основания задается координатами x_1O и y_1O точки O₁ в системе координат OX₁Y₁Z₁, причем y_1O = 0,6 м. Начальное положение цилиндра на основании определяется начальными значениями координат x_2O и y_2O точки O₂ в системе координат OX₁Y₁Z₁. Точка O_н совпадает с начальными положением центра масс цилиндра O₂.

В начальный момент времени к внутренней поверхности дна цилиндра прикладывается переменная нагрузка P(t), определяемая по зависимости (6.1). При этом цилиндр 2 начинает скользить по основанию 1, вызывая вращение последнего вокруг оси шарнира OZ. Движение цилиндра тормозится реакцией R(t) тормозного устройства 3, приложенной к внешней поверхности дна цилиндра. Величина реакции определяется по формуле (6.2). Моменты инерции основания и цилиндра относительно осей O₁z₁ и O₂z₂ равны J₁ и J₂ соответственно.

Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.

Указание. В качестве обобщенных координат выбрать:
1) перемещение точки C по горизонтальной оси 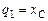, отсчитанное от положения статического равновесия пружины CD;
2) угол поворота j основания 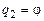, отсчитанный от горизонтали, и 3) перемещение S центра масс цилиндра 2 по направляющей основания 1 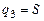, отсчитанное от его начального положения O_н. Начальное значение j = j₀. Длину недеформированной пружины l₂ определить из условия статического равновесия системы в начальный момент времени. Рекомендуемые значения величин приведены в табл. 6.3.

Исходные данные: m₁ – масса основания; m₂ – масса цилиндра. Число степеней свободы: i =s = 3. За обобщенные координаты приняты следующие параметры: 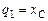; ; 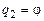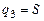. Обобщенные скорости: 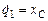; ; 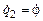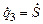. В рассматриваемую механическую систему входят: основание 1 и цилиндр 2, совершающие плоскопараллельное движение относительно неподвижной системы координат OXYZ,

; ;

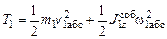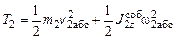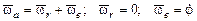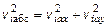; , i=1,2,

где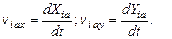

Координаты центра массы основания в матричной форме:

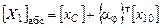(1), или

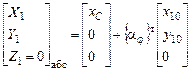, где 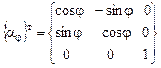, т.е.

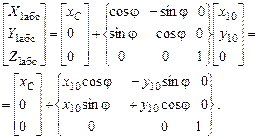
Скорости центра массы основания в матричной форме:

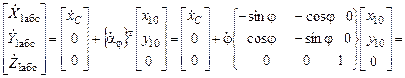
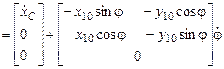, или

;

;

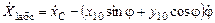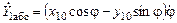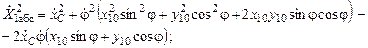
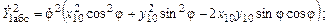
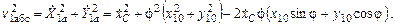
Кинетическая энергия основания в функции обобщенных координат и обобщенных скоростей:

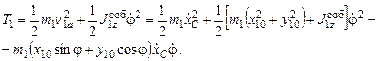
Координаты центра массы цилиндра в матричной форме:

.

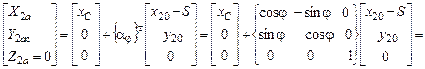
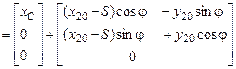Скорости центра массы цилиндра 2 в матричной форме:

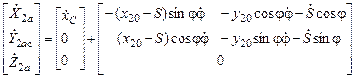, или

;

.

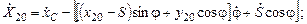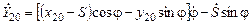их квадраты:

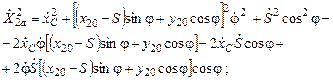
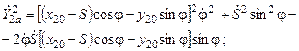
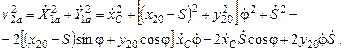
Кинетическая энергия цилиндра в функции обобщенных координат и обобщенных скоростей:

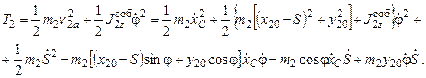
Кинетическая энергия системы

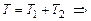
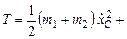
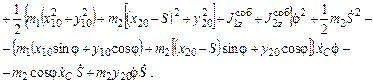
Уравнения Лагранжа второго рода для данной системы:

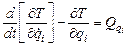
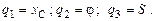
Для :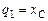

;

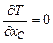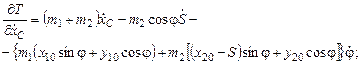
окончательно левая часть уравнения по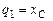

;

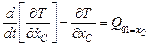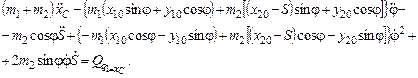
Для :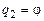

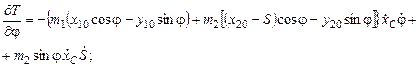
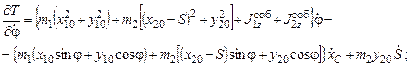
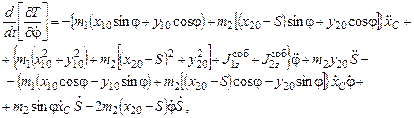
окончательно левая часть уравнения по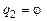

;

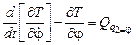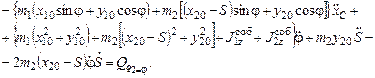
Для :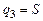

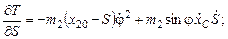
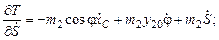
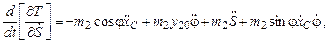
окончательно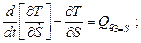

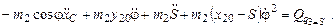
Перепишем уравнения Лагранжа второго рода, оставив в левой части только слагаемые со вторыми производными от обобщенных координат. Все остальные слагаемые перенесем в правую часть уравнения, обозначив их как

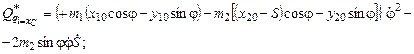
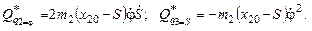
Уравнения Лагранжа второго рода в матричной форме:

,

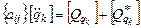где 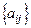– инерционная матрица, 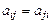, если 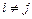, , 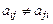если ,

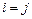или ,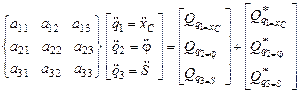

инерционные коэффициенты:

;

;

;

;

.

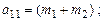
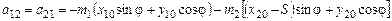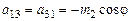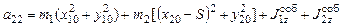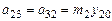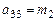Виртуальная работа сил, действующих на рассматриваемую систему:

;

.

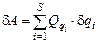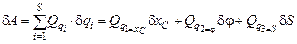Так как обобщённые координаты - независимые друг от друга параметры, то и их вариации тоже независимы. Поэтому, используя принцип замораживания, находим виртуальные работы, соответствующие виртуальным перемещениям поочередно:

1) ,

;

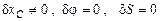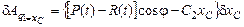2) ,

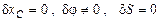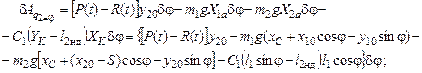
3) ,

.

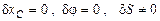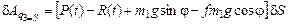Сравнивая множители в выражениях виртуальных работ перед вариациями соответствующих обобщённых координат и в формуле (6.7), находим обобщённые силы, соответствующие обобщённым координатам:

;

.

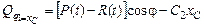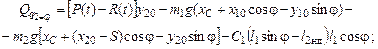
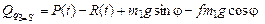Библиографический список

1. Методические указания к решению задач с использованием ЭВМ / Сост. Ж.Н. Андреева; Ч.2. Лен. мех. ин-т. Л., 1988.

2. Динамические задачи артиллерии / Под ред. Н.Н. Худкова. М.: Машиностроение, 1985.

3. Лурье, А.И. Аналитическая механика / А.И. Лурье. М.: Физматгиз, 1947.

4. Постнов, В.А. Численные методы расчета судовых конструкций /
В.А. Постнов. Л.: Судостроение, 1975.

5. Коноплев, В.А. Агрегативная механика систем твердых тел / В.А. Коно-
плев. СПб: Наука, 1996.

6. Теоретическая механика / Под ред. Н.Н.Поляхова. Л.: Изд-во ЛГУ, 1985.

О г л а в л е н и е

Введение. 3

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЕЙСТВИЯ ВЫСТРЕЛА НА АРТИЛЛЕРИЙСКОЕ ОРУДИЕ 5

1.1. Некоторые сведения о методиках расчета динамических моделей объектов вооружения 5

1.2. Выбор и обоснование расчетной схемы.. 6

1.3. Анализ конструкций современных образцов артиллерийских орудий 8

В о п р о с ы для с а м о к о н т р о л я. 11

2. ДВИЖЕНИЕ СИСТЕМЫ ПРИ НАЛИЧИИ СВЯЗЕЙ. УРАВНЕ-НИЯ ЛАГРАНЖА II РОДА ПРИ НЕСТАЦИОНАРНОМ БАЗИСЕ.. 11

2.1. Основные понятия. Несвободное движение точки и механической системы 11

2.2. Связи и их классификация. 12

2.3. Возможные и виртуальные перемещения. 15

2.4. Обобщенные координаты. Число степеней свободы механи-ческой системы 19

2.5. Виртуальная работа силы. Идеальные связи. 23

2.6. Обобщенные силы.. 25

2.7. Уравнения Лагранжа II рода (без вывода) 30

2.8. Последовательность действий при использовании уравнений Лагранжа II рода для решения задач о движении голономных систем.. 33

В о п р о с ы для с а м о к о н т р о л я. 38

3. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ.. 39

3.1. Выбор осей координат. Углы Крылова (корабельные углы). Кинематические уравнения корабельного носителя на вол-нении. 39

3.2. Углы Эйлера. 45

3.3. Формулы преобразования координат. Поворотные матрицы.. 48

3.4. Мгновенная угловая скорость и угловое ускорение. Кинемати-ческие уравнения Эйлера 52

3.5. Скорость и ускорение точек тела. Формула Ривальса. 55

В о п р о с ы для с а м о к о н т р о л я. 57

4. Расчетная работа №1. Вращение твердого тела (корабель-ногона волнении или сухопутного на грунте носителя) вокруг неподвижной точки (регулярная прецессия) 58

5. Расчетная работа №2. Динамика несвободной системы
с двумя степенями свободы.. 72

6. Курсовая работа №3. Расчет динамических моделей объектов вооружения конкретных конструктивно-компоновочных схем.. 80

Указания к выполнению работы.. 80

Схемы конструкций и исходные данные к работе «Динамика несвободной системы с двумя степенями свободы» 83

Схемы конструкций и исходные данные к вариантам курсовой работы повышенной трудности 101

Примеры выполнения курсовой работы.. 111

Библиографический список. 134

Андреева Жаннета Николаевна, Агошков Олег Григорьевич,
Белов Альберт Васильевич