Математические модели с использованием сетей Петри

Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма, асинхронности и иерархичности.

На рис. 4 приводится сети Петри, где Р — конечное непустое множество позиций (состояний); Т — конечное непустое множество переходов (событий), причем 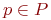и — функции входных и выходных инциденций; 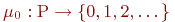— начальная маркировка. Вершины сети 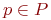изображены кружками, а вершины 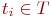— черточками (маркерами). Дуги соответствуют функциям инцидентности позиций и переходов. Точки в кружочках означают заданную начальную маркировку. Число маркеров в позиции равно значению функции 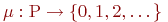. Переход от одной маркировки к другой осуществляется срабатыванием переходов. Переходt может сработать при маркировке 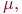если он является возбужденным:

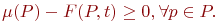(13.10)

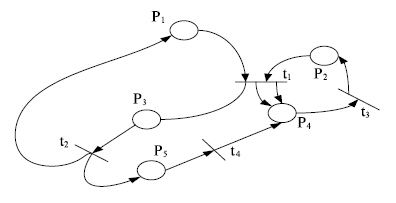
Рис. 4. Сеть Петри

Данное условие показывает, что в каждой входной позиции перехода t число маркеров не меньше веса дуги, соединяющей эту позицию с переходом. В результате срабатывания перехода t, удовлетворяющего условию (13.10), маркировку 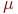заменяют маркировкой 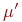по следующему правилу:

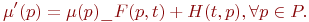(13.11)

По этому правилу в результате срабатывания из всех входных позиций перехода t изымается F(p,t) маркеров и в каждую выходную позицию добавляется H(t,p) маркеров. Это означает, что маркировка 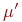непосредственно достижима из маркировки 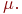Функционирование сети Петри — последовательная смена маркировок в результате срабатывания возбужденных переходов.

Состояние сети в данный момент времени определяется ее текущей маркировкой. Важная характеристика сети Петри — граф достижимости, с помощью которого описываются возможные варианты функционирования сети. Такой граф имеет вершины, которые являются возможными маркировками. Маркировк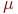и и 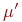соединяются в направлении t дугой, помеченной символами перехода 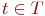или 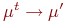. Маркировка 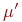такая последовательность переходов: 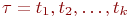является достижимой из маркировки 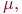если существует, что .

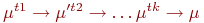В качестве примера рассматривается сеть Петри, изображенная на рис. 4.

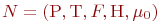, где Р = {Р₁, Р₂, Р₃, Р₄, Р₅},

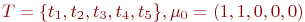. Функции F и Н заданы матрицами 2

P1

P2

P3

P4

P5

H =

t1

t2

t3

t4

t1

t2

t3

t4

F =

P1

P2

P3

P4

P5

Фрагмент графа достижимости для сети Петри приведен на рис. 5.

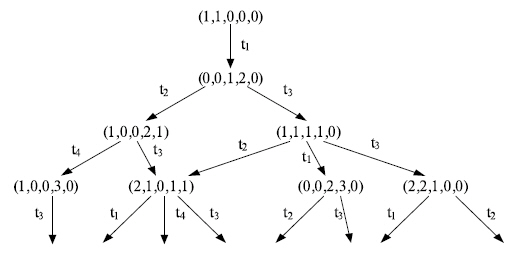
Рис. 5. Фрагмент графа достижимости сети Петри

Структурные модели

Структурные или структурно-логические модели, согласно ГОСТ 14.416-83, подразделяются на табличные, сетевые и перестановочные. Сетевыеопределяются строками булевой матрицы (таблица 3).

Здесь S_i — свойства моделей, влияющих на содержание проектирования; F(S) — набор свойств, если все графы объектов А_к, проектируемых по данной модели, простые пути или цепи, F_g = 1 и F_g = 0 в противном случае; F_n — набор свойств, учитывающих число элементов во всех вариантах объектов A_k ( F_n = 1 — число элементов во всех a_i одинаково, F_n = 0 — в противном случае); 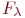— набор свойств, учитывающих отношения между любыми элементами объекта 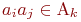во всех вариантах объектов А_k ( 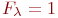— отношение не меняется, 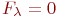— в противном случае); F_а — набор свойств, учитывающих состав элементов a_i в А_k ( F_а = 1 — состав одинаков, F_а = 0 — в противном случае).

Таблица 3.
	Fg	Fa		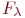Fn
[Si x F(S)] =					S1
				S2
				S3
				S4
				S5
				S6
				S7
				S8
				S9
				S10
				S11
				S12

В матрице (3) модели класса S_i называют табличными. В табличной модели каждому набору свойств F(А_k) соответствует единственный вариант проектируемого объекта А_k, поэтому табличные модели используют для поиска стандартных, типовых и готовых решений. Модели остальных классов применяют для получения типовых унифицированных и индивидуальных проектных решений при наличии их вариантов и необходимости оптимизации решения. Модели классов S₂ , S₅ , S₇ , S₈ и S₁₁ называют сетевыми. Структура элементов сетевой модели описывается ориентированным графом, не имеющим ориентированных циклов. В этой модели может содержаться несколько вариантов проектируемого объекта А_k, однако во всех вариантах сохраняется неизменным соотношение порядка между входящими элементами. Модели классов S₃ , S₄ , S₆ , S₉ , S₁₀ и S₁₂ называютперестановочными. Соотношение порядка между элементами проектируемого объекта А_k в перестановочных объектах обычно задается с помощью графа, содержащего ориентировочные циклы, причем все варианты объектов А_k, проектируемые по перестановочным моделям, различаются порядком между элементами, входящими в них.

Объектом проектирования А_k может быть технологический процесс, операция или технологический переход. Если рассматривать технологический процесс в качестве объекта проектирования, то операции будут элементами. При проектировании операции элементами будут технологические переходы.

Если А_k должен содержать фиксированный набор элементов 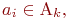то

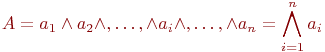
Если А_k может содержать любой элемент 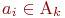, то

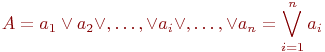
А если какой-либо единственный элемент 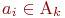, то

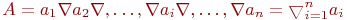
При обработке группы деталей на токарном прутковом автомате с помощью табличной модели устанавливается последовательность обработки поверхностей. Каждая деталь имеет поверхности F₁, F₂, ...., F₈ с определенными свойствами, поэтому состав свойств поверхностей, относящихся к группе деталей, будет

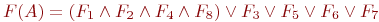
Если ввести совокупность свойств более высокого уровня:

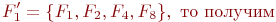
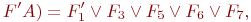
а если совокупность свойств деталей 1-й, 2-й, 3-й групп (соответственно, элементам а₁, а₂, а₃ группы А деталей, т. е. 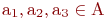), то получим