Теоремы Эйлера и Ферма. Тест Ферма на простоту

В этом пункте будут доказаны важнейшие теоремы теории чисел и показаны их приложения к задачам криптографии.

Теорема Эйлера.

При m > 1, (a, m) = 1 a^φ(m) ≡ 1 (mod m).

Доказательство:

Если x пробегает приведенную систему вычетов x = r₁, r₂,…,r_c (c = φ(m)), составленную из наименьших неотрицательных вычетов, то в силу того, что (a,m)=1, наименьшие неотрицательные вычеты чисел ax = ρ₁, ρ₂,…, ρ_c будут пробегать ту же систему, но, возможно, в другом порядке (это следует из утверждения 2 пункт 3). Тогда, очевидно,

r₁·…·r_c = ρ₁·… ·ρ_c *

Кроме того, справедливы сравнения

ar₁ ≡ ρ₁(mod m), ar₂ ≡ ρ₂(mod m), … , ar_c ≡ ρ_c(mod m).

Перемножая данные сравнения почленно, получим

a^c ·r₁ ·r₂ ·…·r_c ≡ ρ ₁·…· ρ _c(mod m)

Откуда в силу (*) получаем

a^c ≡ 1 (mod m)

А поскольку количество чисел в приведенной системе вычетов по модулю m есть φ(m), то есть c = φ(m), то

a^φ(m) ≡ 1 (mod m).

□

Теорема Ферма (малая)

р – простое, p не делит a a^p–1 ≡ 1 (mod m)

Доказательство: по теореме Эйлера при m=p.

Важное следствие:

a^p ≡ a (mod p) 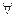a, в том числе и для случая p\a.

Теорема Эйлера применяется для понижения степени в модулярных вычислениях.

Пример:

10¹⁰⁰ mod 11 = 10^9∙11+1 = 10⁹⁺¹ mod 11 = (–1)¹⁰ mod 11 = 1.

Следствие:

Если 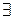a: 0 < a < p, для которого a^p–1 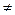1 (mod p) p – составное.

Отсюда –

Тест Ферма на простоту

Вход: число n – для проверки на простоту, t – параметр надежности.

1. Повторяем t раз:

а) Случайно выбираем a 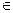[2, n-2]

б) Если a^n–1 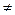1 (mod n) «n – составное». Выход.

2. «n – простое с вероятностью 1–ε^t »

Этот тест может принять составное число за простое, но не наоборот.

Вероятность ошибки есть ε^t, где ε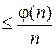

В случае составного числа n, имеющего только большие делители, ε 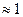, то есть существуют числа, для которых вероятность ошибки при проверке их на простоту тестом Ферма близка к 1.

Для теста Ферма существуют так называемые числа Кармайкла – такие составные числа, что 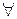a: (a,n) = 1 a^n–1 ≡ 1(mod n). То есть числа Кармайкла – это такие составные числа, которые всегда принимаются тестом Ферма за простые, несмотря на то, как велико число t – параметр надежности теста.

Теорема Кармайкла

n – число Кармайкла 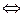1) n свободно от квадратов (т.е. n = p₁∙p₂∙…∙p_k);

2) (p_i – 1)\(n – 1), i = 1,…,k ;

3) k .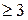

Наименьшее известное число Кармайкла n=561 = 3∙11·17

3.7. Применение теоремы Эйлера в RSA:

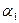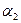Если известно разложение числа на простые сомножители a = p₁ p₂ … p_n 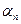, то легко вычислить функцию Эйлера φ(a).

Отсюда вывод: сложность вычисления функции Эйлера не выше сложности задачи факторизации .

Покажем, что в случае n=pq (p,q – простые числа, p 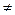q) задачи нахождения функции Эйлера и факторизации эквивалентны. (то есть в случае, когда n – модуль RSA).

Учтем, что φ(n) = (p – 1)(q – 1). Тогда имеем систему

.

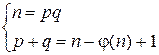Зная n и φ(n), находим p и q из системы, приведенной выше, следующим образом:

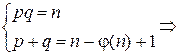
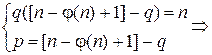
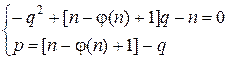
Первое уравнение системы является квадратным уравнением относительно q,

q = 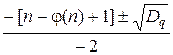, где D_q = [n– φ(n)+1]² – 4n.

Подставляя полученное q во второе уравнение системы, находим p.

Видим, что при нахождении чисел p, q по известным n, φ(n) применяются только «дешевые» в смысле времени операции – сложение, деление на 2. Только при вычислении дискриминанта приходится применять возведение в степень, а при вычислении q – извлечение квадратного корня. Однако эти операции производятся однократно, поэтому временные затраты не столь существенны.

Итак, для модуля RSA задачи нахождения функции Эйлера и факторизации равносложны.

Формулировка теоремы Эйлера для RSA:

n = pq; p≠q; p, q – простые числа 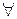a выполняется a^kφ(n)+1≡ a (mod n).

(на самом деле n может быть просто свободно от квадратов, то есть произведением произвольного количества различных простых чисел)

Доказательство:

Возможны два случая:

1) (a, n) = 1 по теореме Эйлера a^φ(n) ≡ 1 (mod n)

a^kφ(n)+1 = 1^k ∙a ≡ a (mod n).

2) (a, n) ≠ 1, n не делит a в силу основного свойства простых чисел, либо p\ a, либо q \ a.

Не нарушая общности, предположим, что p\a, q не делит a.

Тогда по теореме Ферма, a^kφ(n)+1≡a(mod p),

q^q–1≡1 (mod q) a^kφ(n)+1≡1^k(p–1)·a ≡ a (mod q).

Итак, a^kφ(n)+1 ≡ a (mod p), a^kφ(n)+1≡ a (mod q). Отсюда по св-ву сравнений №12, a^kφ(n)+1≡ a(mod НОК(p,q)). В силу простоты p и q, НОК(p,q)=pq=n, значит

a^kφ(n)+1≡ a (mod n).

3) n\a a≡0(mod n) a^kφ(n)+1≡0≡a(mod n).

□

Примечание:

Если вместо φ(n) в теореме Эйлера для RSA взять НОК(p–1, q–1), теорема все равно будет верна.

Применение теоремы Эйлера в RSA:

Напомним, что криптосистема RSA является системой с открытым ключом. В качестве параметров системы выбираются различные большие простые числа p и q, вычисляется n=pq, φ(n)=(p–1)(q–1), выбирается число e: 2<e<n, (e, φ(n))=1 и вычисляется d=e^-1(mod φ(n)). В качестве открытого ключа берется пара (n, e), в качестве закрытого, хранимого в секрете, четверка (p, q, φ(n), d).

Для того, чтобы зашифровать открытый текст x, абонент, пользуясь открытым ключом, вычисляет зашифрованный текст y по следующей формуле:

y = x^e mod n.

Для того, чтобы осуществить расшифрование, владелец секретного ключа вычисляет

x = y^d mod n.

В результате такого расшифрования действительно получится открытый текст, поскольку y^d mod n=x^ed mod n=x^{ed mod φ(n)}mod n =x¹ mod n=x.

Без знания простых сомножителей p и q сложно вычислить значение функции Эйлера φ(n), а значит, и степень d, в которую следует возводить зашифрованный текст, чтобы получить открытый.

Более того, знание простых сомножителей p и q может значительно облегчить процедуру возведения шифрованного текста y в степень d. Действительно, пользуясь теоремой Эйлера для RSA, можем понизить степень d. Разделим d на φ(n) с остатком:

d=kφ(n)+r

x=y^d mod n= y^kφ(n)+r mod n= y^r mod n.

Еще более можно понизить степень, используя НОК(p–1,q–1)= 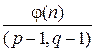вместо φ(n).

Пример:

n=19∙23=, φ(n)=18∙22=396, d=439.

НОК(18,22)=18∙22/2=198.

d mod φ(n)=43. d mod НОК(p–1,q–1)=43.

Число d=439 в двоичном представлении есть 110110111. Поэтому возведение в степень d c применением дихтономического алгоритма (см. гл.2) требует 8 возведений в квадрат и 6 умножений чисел.

Число 43 в двоичном представлении есть 101011. Возведение в степень 43 требует 5 возведений в квадрат и 3 умножения чисел. Кроме того, для вычисления φ(n) требуется 1 операция умножения.

Таким образом, для данного примера экономия времени составляет 2 сложные операции.

В случае больших простых делителей числа n экономия оказывается более существенной.