Важнейшие замкнутые классы Алгебры Логики
Класс Т0 – класс булевых функций, сохраняющих константу «0», то есть это такие функции от f(x1, …, xn), что f(0, …, 0) = 0.
Пример:
1) Принадлежащие Т0: &, Ú, x.
2) Не принадлежащие Т0: x ® y,  .
.
| x1 | … | xn | f | Þ 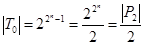 | ||
| … | ||||||
| … | 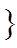 | 2n - 1 | ||||
| ………… | ||||||
| … |
Теорема.
Т0 – замкнутый класс.
Доказательство: T0 = |T0| Û 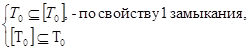
Докажем: [T0] Í T0, Ф Î [T0] 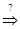 Ф Î T0. Ф = f(f1, …, fs) = f(f1(x1, …, xn), …, fs(x1, …, xn)), f1, …, fs Î T0. Следовательно, Ф(0, …, 0) = f(f1(0, …, 0), …, fs(0, …, 0)) = f(0, …, 0). Так как каждая функция f1, …, fs сохраняет «0», то Ф Î T0.
Ф Î T0. Ф = f(f1, …, fs) = f(f1(x1, …, xn), …, fs(x1, …, xn)), f1, …, fs Î T0. Следовательно, Ф(0, …, 0) = f(f1(0, …, 0), …, fs(0, …, 0)) = f(0, …, 0). Так как каждая функция f1, …, fs сохраняет «0», то Ф Î T0.
Класс Т1 – класс всех булевых функций, сохраняющих константу «1», то есть Т1: f(1, …, 1) = 1.
Пример:
1. Принадлежащие Т1: x & y, x Ú y, x, x ® y.
2. Не принадлежащие Т1: x Å y,  .
.
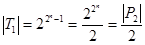 (T0 Ç T1 ¹ Æ)
(T0 Ç T1 ¹ Æ)
Класс S – класс самодвойственных функций, то есть f* = f Þ f – самодвойственная.
Пример:
1) Принадлежащие S: x,  .
.
2) Не принадлежащие S: x & y, x Ú y, x ® y.
f Í S: f*(x1, …, xn) 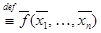 = [f Í S] = f(x1, …, xn).
= [f Í S] = f(x1, …, xn).
Определение. Наборы (a1, …, an) и 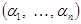 – противоположные. На таких наборах самодвойственная функция принимает противоположные значения. Самодвойственная функция полность определяется на первых n / 2 строках таблицы.
– противоположные. На таких наборах самодвойственная функция принимает противоположные значения. Самодвойственная функция полность определяется на первых n / 2 строках таблицы.
Теорема.
S – замкнутый класс.
Доказательство: S – замкнутый класс.
Доказательство: S = |S| Û 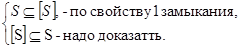
Ф Î [S] 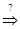 Ф Î S, f1, …, fl Î S. Ф = f(f1, …, fn) = f(f1(x1, …, xn), …, fl(x1, …, xn)). Рассмотрим Ф*( x1, …, xn) = f*(f1*(x1, …, xn), …, fl*(x1, …, xn)) = [xi* = fi, i = 1, 2, …, n, f* = f] = f(f1(x1, …, xn), …, fl(x1, …, xn)) = Ф*( x1, …, xn) Þ Ф – самодвойственная.
Ф Î S, f1, …, fl Î S. Ф = f(f1, …, fn) = f(f1(x1, …, xn), …, fl(x1, …, xn)). Рассмотрим Ф*( x1, …, xn) = f*(f1*(x1, …, xn), …, fl*(x1, …, xn)) = [xi* = fi, i = 1, 2, …, n, f* = f] = f(f1(x1, …, xn), …, fl(x1, …, xn)) = Ф*( x1, …, xn) Þ Ф – самодвойственная.
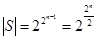
Лемма ( О не самодвойственных функциях).
Если функция f(x1, …, xn) – не является самодвойственной, то из нее путем подстановки функций x и  можно получить не самодвойственную функцию от одной переменной, то есть константу (
можно получить не самодвойственную функцию от одной переменной, то есть константу ( 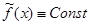 ).
).
Доказательство: Так как f Ï S Þ $(a1, …, an): f(a1, …, an) = 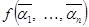 ,
, 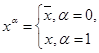 , x1 ~
, x1 ~ 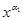 , xn ~
, xn ~ 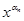 . Заметим, что
. Заметим, что 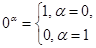 , то есть
, то есть 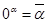 и 1a = a. Рассмотрим функцию
и 1a = a. Рассмотрим функцию 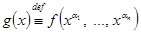 . Докажем, что g(x) º Const. Для этого рассмотрим g(0) и g(1): g(0) =
. Докажем, что g(x) º Const. Для этого рассмотрим g(0) и g(1): g(0) = 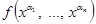 =
= 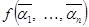 = f(a1, …, an) =
= f(a1, …, an) = 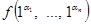 = g(1) Þ g(0) = g(1) Þ g(x) º Const.
= g(1) Þ g(0) = g(1) Þ g(x) º Const.
Класс М – класс монотонных функций.
Определение. Пусть набор 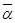 = (a1, …, an), f(
= (a1, …, an), f( 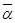 ) = f(a1, …, an). Для любых
) = f(a1, …, an). Для любых 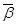 = (b1, …, bn) выполнено отношение предшествования, если ai ≤ bi, для "i = 1, 2, …, n (
= (b1, …, bn) выполнено отношение предшествования, если ai ≤ bi, для "i = 1, 2, …, n ( 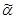
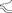
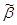 ) или bi ≤ ai, для "i = 1, 2, …, n (
) или bi ≤ ai, для "i = 1, 2, …, n ( 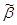
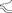
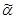 ).
).
Пример: Наборы:
(0, 1, 0, 1) 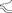 (1, 1, 0, 1)
(1, 1, 0, 1)
(0, 1, 0, 1) ? (1, 0, 0, 1) – не находятся в отношении предшествования.
Определение. Если 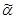
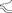
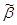 ,
, 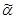
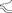
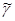 Þ
Þ 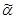
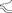
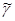 (Свойство транзитивности).
(Свойство транзитивности).
Определение. Функция f(x1, …, xn) принадлежит классу монотонных функций, если для " 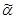
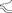
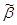 имеет место неравенство f(
имеет место неравенство f( 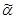 )
) 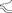 f(
f( 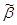 ).
).
Пример:
1) Принадлежит М: 0, 1, x & y, x Ú y.
2) Не принадлежит М:  , x ® y, x Å y.
, x ® y, x Å y.
В Алгебре логики монотонная функция является только монотонно-возрастающей.
Теорема.
Класс М – замкнутый.
(без доказательства)
Лемма (О немонотонной функции).
Если немонотонная, то из нее путем подстановки констант «0» и «1» и функции x можно получить немонотонную функцию от одной переменной, (  ).
).
Доказательство: Так как f Ï М Þ $ 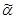 и
и 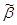 ,
, 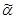
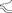
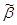 : f(
: f( 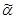 ) > f(
) > f( 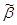 ). Рассмотрим
). Рассмотрим 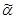 = (a1, …, ai-1, 0, ai+1, …, an) и
= (a1, …, ai-1, 0, ai+1, …, an) и 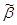 = (a1, …, ai-1, 1, ai+1, …, an). Рассмотрим функцию g(x) = f(a1, …, ai-1, x, ai+1, …, an), g(0) = f(
= (a1, …, ai-1, 1, ai+1, …, an). Рассмотрим функцию g(x) = f(a1, …, ai-1, x, ai+1, …, an), g(0) = f( 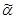 ) > g(1) = f(
) > g(1) = f( 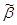 ) Þ
) Þ 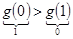 Þ g(x) =
Þ g(x) =  .
.
Класс L – класс линейных функций, то есть L = { C0 Å C1x1 Å … Å Cnxn }.
Пример:
1) Принадлежащие L: 0, 1, x, 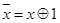 .
.
2) Не принадлежащие L: x& y, x Ú y, x ® y.
[L] = L
Для каждого n (число переменных) существует по 2 линейных функции, то есть x1 Å … Å xn и x1 Å … Å xn Å 1.
|L| = 2n
Лемма (О нелинейной функции).
Если f(x1, …, xn) не является линейной, то из нее путем подстановки констант «0» и «1» функций x и  , а также, может быть, путем навешивания отрицаний к функции f, можно получить нелинейную функцию от двух переменных, то есть x & y.
, а также, может быть, путем навешивания отрицаний к функции f, можно получить нелинейную функцию от двух переменных, то есть x & y.
Доказательство: Так как f Ï L, то есть полином Жегалкина обязательно содержит конъюнкцию (x & y) Þ получить x & y. Доказательство: без ограничения общности можно считать, что в этих конъюнкциях можно читать существенным x1 & x2, то есть ПЖ(f) = x1x2f1(x3, …, xn) Å x1f2(x3, …, xn) Å x2f3(x3, …, xn) Å f4(x3, …, xn). Так как Полином Жегалкина – единственный, то f1(x3, …, xn) ¹ 0. Выберем набор значений (x3, …, xn), f(x3, …, xn) = 1. Пусть j(x1, x2) = f(x1, x2, a3, …, an) = x1x2 Å ax1 Å bx2 Å g, где a = f2(x3, …, xn), b = f3(x3, …, xn), g = f4(x3, …, xn) (a, b, g = 0 или 1). Сделаем подстановку: x1 ~ x1 Å C1, x2 ~ x2 Å C2. j(x1 Å C1, x2 Å C2) = (x1 Å C1)( x2 Å C2) b a(x1 Å C1) Å b(x2 Å C2) Å g = x1x2 Å C2x1 Å C1x2 Å C1C2 Å ax1 Å aC1 Å bx2 Å bC2 Å g = [C2 = a, C1 = b] = x1x2 Å ab Å ab Å ab Å g = x1x2 Å ab Å g = 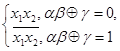 . Вывод: x1x2 = j(x1 Å C1, x2 Å C2) Å d = f(x1 Å C1, x2 Å C2, a3, …, an) Å
. Вывод: x1x2 = j(x1 Å C1, x2 Å C2) Å d = f(x1 Å C1, x2 Å C2, a3, …, an) Å 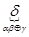 .
.
(Лекция 11)
Существует два способа определения f Î L:
1) Записать Полином Жегалкина для f и выяснить – есть ли конъюнкция. Тогда f Î L.
2) а) Исключить фиктивные переменные из f;
б) Построить диаграмму для полученной функции.
Для функции двух переменных (x Å y):
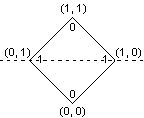
Функция является линейной, если на противоположных слоях разные значения.
Для функции трех переменных:
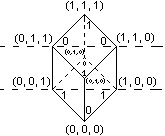
f Î L значения функции на слоях чередуются.
Замечание. Все рассмотренные пять классов – неполные и попарно-различные, то есть существует булева функция, не принадлежащая ни одному из этих классов и в то же время есть функция, принадлежащая одному из любых двух классов, но не принадлежащая другому.
Пример:
| T0 | T1 | S | M | L | |
| + | - | - | + | + | |
| - | + | - | + | + | |
 | - | - | + | - | + |
Вывод: Для проверки полноты системы булевых функций можно ограничиться рассмотренными пятью замкнутыми классами.
Фундаментальная теорема Алгебры логики
(Критерий полноты системы булевых функций)
(Теорема Поста о функциональной полноте)
Система булевых функций F является полной тогда и только тогда, когда она целиком не содержится ни в одном из пяти замкнутых классов: Т0, Т1, S, M, L.
Доказательство:
1) Необходимость. Пусть F – полная система булевых функций. Доказываем методом «от противного». Допустим, F содержится в одном из пяти замкнутых классов (F Í X) Þ [по свойству замыкания] Þ [F] Í [X] = X (так как Х – замкнутый класс) Þ Замыкание этой системы совпадает с множеством булевых функций (P2 = [F] Í X), то есть P2 Í X, но X Í P2 (изначально), то есть X = P2, что неверно из определения одного из замкнутых классов. Значит, наше допущение неверно и F целиком содержится в одном из пяти замкнутых классов.
2) Достаточность. Пусть F не содержится ни в одном из пяти замкнутых классов. Тогда, из системы F можно выделить подсистему F’, содержащую не более пяти функций, которые также обладают этим свойством, то есть F’ = {f1, f2, f3, f4, f5}, причем f1 Ï T0, f2 Ï T1, f3 Ï S, f4 Ï M, f5 Ï L. Докажем, что F содержит  и & (Известно, что {Ø, &} – полная система). Поскольку f1 Ï T0 Þ f1(0, …, 0) = 1 Þ f1(1, …, 1) =
и & (Известно, что {Ø, &} – полная система). Поскольку f1 Ï T0 Þ f1(0, …, 0) = 1 Þ f1(1, …, 1) = 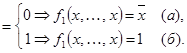
В случае (а) есть  . Берем функцию f3 Þ [по лемме о не самодвойственной функции] Þ получаем константу. Так как есть
. Берем функцию f3 Þ [по лемме о не самодвойственной функции] Þ получаем константу. Так как есть  , то получаем вторую константу. Таким образом, у нас есть (0, 1,
, то получаем вторую константу. Таким образом, у нас есть (0, 1,  , f5) Þ [по лемме о нелинейной функции] Þ x1 & x2. Получим {Ø, &}. Пункт (а) доказан.
, f5) Þ [по лемме о нелинейной функции] Þ x1 & x2. Получим {Ø, &}. Пункт (а) доказан.
Докажем пункт (б). f2(1, …, 1) = 0 Þ f1(1, …, 1) = 1. (0, 1, f4) Þ [по лемме о немонотонной функции] Þ получим  . Теперь получим конъюнкцию аналогично пункту (а).
. Теперь получим конъюнкцию аналогично пункту (а).
Таким образом, мы выразили функции Ø и & через функции системы F’. Но известно, что система {Ø, &} – полная. Значит, по теореме о сведении вопроса о полноте системы одной функции к вопросу о полноте другой. Отсюда F’ – полная Þ F – полная.
Пример: x ® y, x ~ y.
| x | y | x ® y | x ~ y | T0 | T1 | S | M | L | x ~ y = 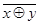 = x Å y Å 1 x ® y = xy Å x Å1 = x Å y Å 1 x ® y = xy Å x Å1 | |||
| ® | – | + | – | – | + | |||||||
| ~ | – | + | – | – | + | |||||||
 | – | – | + | – | + | |||||||
Данная система содержится в Т1. Следовательно, по критерию полноты эта система неполная.
Можно ли добавить к этой системе такую функцию, чтобы система стала полной?
Система {Ø, ®, ~}- полная, то есть [{Ø, ®, ~}] = P2.
Можно ли исключить из этой системы такую функцию, чтобы система стала полной?
[{Ø, ®}] = P2 Þ {Ø, ®} – полная.
Определение. Полная система булевых функций, которая при удалении из нее любой функции становится неполной, называется базисом.
Примеры базисов:
1) {x / y}
2) {x & y,  }, {x Ú y,
}, {x Ú y,  }
}
3) {1, x & y, x Å y}
Из примера (2) следует, что система {x & y, x Ú y,  } – полная, но не базис.
} – полная, но не базис.
Система:
| T0 | T1 | S | M | L | Найдем базис: {0, 1, &} Ì М Þ неполная {0, 1, Å} Ì L Þ неполная {0, &, Å} Ì T0 Þ неполная {1, &, Å} Þ полная и является базисом | ||
| + | -- | -- | + | + | |||
| -- | + | -- | + | + | |||
| & | + | + | -- | + | -- | ||
| Å | + | -- | -- | -- | + |
Следствие 1 из Теоремы Поста.
Каждый базис в алгебре логики состоит не более чем из 4-х функций.
Доказательство:
Пусть f1 Ï T0, f2 Ï T1, f3 Ï S, f4 Ï M, f5 Ï L Þ {f1, f2, f3, f4, f5} – полная по теореме Поста. Докажем, что из этой системы можно удалить одну функцию и система останется полной.
(а) f1(1, …, 1) = 0 Þ f1 Ï M Þ Удаляем f4 Þ {f1, f2, f3, f5} – полная.
(б) f1(1, …, 1) = 0 Þ f1 Ï S Þ Удаляем f3 Þ {f1, f2, f4, f5} – полная.
Следствие доказано.
Определение. Класс А называется предполным, если А – неполный, но при добавлении любой f Ï A он становится полным.
Следствие 2 из Теоремы Поста.
В алгебре логики пять предполных классов.
Доказательство:
1) Докажем, что в алгебре логики нет других предполных классов, методом «от противного». Допустим Х – предполный класс, не совпадающий ни с одним из этих пяти. Х – неполный, но содержится в одном из пяти замкнутых классов (Y) по Теореме Поста. X ¹ Y Þ X Ì Y Þ $f Î Y: f Ï X. но после добавления к классу Х {f È X} Í Y Þ [По Теореме Поста] Þ f È {X} – неполная. Получили противоречие с тем, что Х – предполный. Таким образом, других предполных классов в алгебре логики нет.
2) Докажем. Что рассмотренные нами замкнутые классы – предполные. Эти классы не полны по Теореме Поста, так как каждый их них содержится сам в себе. Докажем, что при добавлении любой булевой функции они станут полными, методом «от противного». Пусть Z – один их этих пяти классов. Рассмотрим функцию f Ï Z. Предположим, что Z – не предполный. Тогда после добавления функции f он становится неполным. Если он неполный, то по Теореме Поста Z È {f} Í W, где W – другой из этих пяти классов. Отсюда получается, что Z Í W. Это противоречит определению одного из пяти замкнутых классов. Перебирая последовательно все пять замкнутых классов докажем, что все они предполные.
