Замкнутые классы логических функций
Рассмотрим множество А логических функций, обладающих некоторым свойством. Пусть G(Y1,Y2,...,Yk)ÎA и Fi(X1,X2,...,Xn)ÎA, i=1,2,...,k. Произведем суперпозицию функций G и F :
G[F1(X1,...,Xn),...,Fk(X1,...,Xn)] = H(X1,...,Xn)
Если H(X1,...,Xn)ÎA, то А называется замкнутым классом логических функций по отношению к рассматриваемому свойству.
Различают пять «замечательных» свойств, по которым логические функции образуют замкнутые классы.
1. Свойство сохранять нуль. Это свойство заключается в следующем: F(0,..,0)=0. Например, X1X2, X1+X2, X1 Å X2.
Примеры функций, не обладающих свойством сохранять нуль: X1®X2, X1~X2, X1/X2 . Докажем замкнутость класса функций, сохраняющих нуль.
Пусть G(0,...,0)=0 и Fi(0,...,0)=0. Тогда G[F1(X1,...,Xn),...,Fk(X1,...,Xn)] = =G[(0,...,0),...,Fk(0,...,0)]=G(0,...,0)=0 , т.е. H(0,...,0)=0. Что и требовалось доказать.
2. Свойство сохранять единицу. Это свойство заключается в следующем: F(1,...,1)=1.
Например, X1X2, X1+X2, X1®X2.
Примеры функций, не обладающих этим свойством: X1 Å X2, X1/X2.
Замкнутость класса функций, сохраняющих единицу, может быть доказана таким же образом, как и замкнутость класса функций, сохраняющих нуль.
3. Самодвойственность. Введем сначала понятие двойственности. Пусть задана функция F(X1,X2,...,Xn). Двойственной по отношению к функции F называется функция F*, определяемая следующим образом:
F*(X1,X2,...,Xn)= 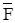 (
( 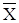 1,
1, 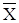 2,...,
2,..., 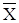 n).
n).
Например, F = X + Y, тогда F*= 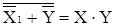 .
.
Самодвойственной функцией называется такая функция, для которой справедливо равенство:
F(X1,X2,...,Xn)= 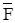 (
( 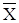 1,
1, 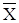 2,...,
2,..., 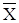 n).
n).
Применив операцию отрицания к левой и правой частям последнего равенства, получим:
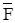 (X1,X2,...,Xn) = F(
(X1,X2,...,Xn) = F( 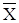 1,
1, 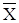 2,...,
2,..., 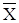 n).
n).
Пример самодвойственной функции:
F=X1X2+X1X3+X2X3.
Действительно, 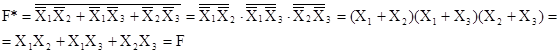
Доказательство замкнутости класса самодвойственных функций.
Пусть 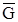 (Y1,..., Yn) и
(Y1,..., Yn) и 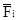 (X1,..., Xn)=
(X1,..., Xn)= 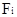 (
( 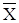 1,...,
1,..., 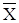 n). Произведем суперпозицию функций G и Fi:
n). Произведем суперпозицию функций G и Fi: 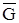 [F1(X1,..., Xn) ,..., Fk(X1,..., Xn)] = G[
[F1(X1,..., Xn) ,..., Fk(X1,..., Xn)] = G[ 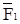 (X1,..., Xn),...,
(X1,..., Xn),..., 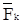 (X1,..., Xn)] = G[F1(
(X1,..., Xn)] = G[F1( 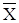 1,...,
1,..., 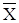 n),...,Fк(
n),...,Fк( 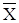 1,...,
1,..., 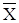 n)] = H(
n)] = H( 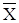 1,...,
1,..., 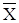 n),
n),
т.е. 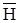 (X1,...,Xn) = H(
(X1,...,Xn) = H( 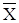 1,...,
1,..., 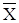 n).
n).
4. Монотонность. Для того чтобы определить монотонную логическую функцию введем критерий сравнения двух наборов аргументов.
Если значение каждого аргумента одного набора больше или равно значению того же аргумента второго набора, то говорят, что первый набор не меньше второго. При этом предполагается, что 0 ³ 0; 1 ³ 0; 1 ³ 1.
Например, (1,1,0,1) ³ (0,1,0,1). Не всякие наборы являются сравнимыми. Например, наборы (0,1) и (1,0) или (0,1,0,1) и (1,0,1) несравнимы.
Логическая функция называется монотонной, если при любом возрастании набора значение этой функции не убывает. При этом рассматриваются только сравнимые наборы. Примеры монотонных функций: XY, X+Y, Примеры функций, не обладающих свойством монотонности: X~Y, X®Y, XÅY. Докажем, что по свойству монотонности функции образуют замкнутый класс.
Пусть функции G(Y1,..., Yn) и Fi(X1,..., Xn)- монотонные. Произведем суперпозицию функций G и F :
G[F1(X1,..., Xn),..., Fk(X1,..., Xn)] = H(X1,..., Xn)
Найдем значения функций Fi и функции G на некотором наборе X1,..., Xn, а затем увеличим этот набор. Так как функции Fiмонотонные, то их значения либо увеличатся, либо останутся без изменения. Так как функция Gмонотонная, то ее значение либо увеличится, либо останется без изменения. Из этого следует, что значение функции Нпри увеличении набора либо увеличится, либо останется без изменения, т.е. функция Hтоже является монотонной, что и требовалось доказать.
5. Линейность. Логическая функция называется линейной, если она может быть представлена полиномом первой степени, т.е. записана в виде F(X1,X2,..., Xn) = A0 Å
Å A1X1 Å A2X2 Å ... Å AnXn,
где A0, A1,..., An - коэффициенты, равные нулю или единице.
Примеры линейных функций: X Å Y, X ~Y = 1 Å X Å Y. .
Покажем, что по свойству линейности функции образуют замкнутый класс. Пусть функции G(Y1,..., Yk) и Fi(X1,..., Xn)- линейные. Представим их в виде линейных полиномов:
G = A0 Å A1Y1 Å A2Y2 Å ... Å AkYk,
Fi = B0i Å B1i Å B2i Å ... Å BniXn.
Подставив функции Fiвместо аргументов Yi в функцию G получим выражение, в котором постоянные коэффициенты Ai умножаются на линейные функции. При этом получатся снова линейные функции. Приведя подобные члены, получим функцию H(X1,..., Xn) в виде линейного полинома.
Из этого следует, что по свойству линейности функции образуют замкнутый класс.
Рассмотрим пример. 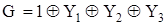 ; F1=X1ÅX2ÅX3; F2=X2ÅX3; F3=1ÅX3. Произведем суперпозицию функций G и Fi:
; F1=X1ÅX2ÅX3; F2=X2ÅX3; F3=1ÅX3. Произведем суперпозицию функций G и Fi:
G=1ÅX1ÅX2ÅX3ÅX2ÅX3Å1ÅX3=X1ÅX3.
3.7. Функционально полные системы
