Энергия заряженного конденсатора

Формулировка

Пусть постоянный ток 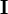течёт по контуру γ, находящемуся в вакууме, 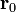— точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)

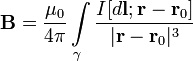
Направление 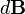перпендикулярно 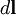и 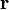, то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление 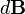, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора 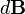определяется выражением (в системе СИ)

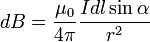
Векторный потенциал даётся интегралом (в системе СИ)

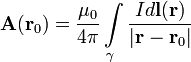
К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются линейными

Принцип суперпозиции магнитных полей: магнитная индукция 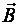в любой точке магнитного поля проводника с током равна векторной сумме магнитных индукций 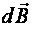, созданных в этой точке всеми элементами 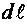проводника с током, т. е.

,

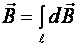2.1. Энергия заряженного проводника и конденсатора. Энергия электрического поля

Энергия электростатического поля.

Энергия заряженного плоского конденсатора E_к равна работе A, которая была затрачена при его зарядке, или совершается при его разрядке.

A = CU²/2 = Q²/2С = QU/2 = E_к.

Поскольку напряжение на конденсаторе может быть рассчитано из соотношения:

U = E*d,
где E - напряженность поля между обкладками конденсатора,
d - расстояние между пластинами конденсатора,

то энергия заряженного конденсатора равна:

E_к = CU²/2 = ee₀S/2d*E²*d² = ee₀S*d*E²/2 = ee₀V*E²/2,
где V - объем пространства между обкладками конденсатора.

Энергия заряженного проводника

Как известно, заряд сосредоточивается на поверхности проводника, причем поверхность проводника эквипотенциальна. Разбивая эту поверхность на маленькие участки, каждый из которых имеет заряд Δq, и учитывая, что потенциал в месте расположения каждого из зарядов одинаков, имеем

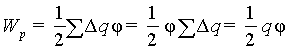(6.7)

Так как емкость проводника C=q/φ , то выражение (6.7) может быть также представлено, как

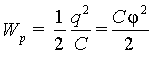(6.8)

Энергия заряженного конденсатора

Пусть заряд +q находится на обкладке с потенциалом φ₁ а заряд -qна обкладке с потенциалом φ₂. Тогда на основании тех же рассуждений, которые привели к выражению (6.7), получим

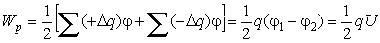(6.9)

где U - разность потенциалов на обкладках конденсатора. Аналогично переходу от (6.7) к (6.8) выражение для энергии конденсатора может быть представлено также в виде