Составление матрицы коэффициентов условных уравнений. Окончательные вычисления

Для решения условных уравнений на ПЭВМ представляют коэффициенты уравнений в виде матрицы (табл. 12).

Уравнительные вычисления производятся по вышеописанному алгоритму с помощью соответствующих программ (программ, составленных студентом, MathCad и др.) в присутствии оператора или преподавателя, с представлением результатов промежуточных и окончательных вычислений.

Уравнительные вычисления могут производится по вышеописанному алгоритму с помощью математической программы Mathсad.

Технология образования векторов и матриц в Mathсad состоит в выполнении следующих действий:

· ввод имени матрицы или вектора (обязательно с заглавной буквы, например: В) и одновременное нажатие клавиш <Shift>+<Ж>, на экране появятся соответственно символы B:=;

· установка размеров вектора или матрицы. Нажимая набор клавиш <Ctrl>+<M>или щелкая мышью по кнопке матрицы панели инструментов Matrix, вызываем окно Insert Matrix. В диалоговом окне указываем число строк вектора или матриц в поле Rows (Строки) и число столбцов в поле Columns (Столбцы). Если число столбцов равно единице, то образуется вектор. После щелчка по кнопке ОК на экране появится пустой шаблон вектора или матрицы;

· ввод элементов вектора или матрицы в пустые маркеры.

Также полезно знать, что нумерация элементов матрицы начинается с нуля, а не с единицы как принято в алгебре.

Можно изменить размер матрицы, вставляя и удаляя строки и столбцы:

1. Щелкните мышью на нужном элементе матрицы (Mathсad вставляет строки и столбцы в направлении вправо и вниз от выделенного элемента матрицы, а удаляет в том же направлении, включая строку и столбец с выделенным элементом).

Таблица 12 Матрица коэффициентов условных уравнений
Номер уравне-ния	Коэффициенты при поправках в углы	W²
																			+3,2
																			+1,3
																			+0,5
																			-4,4
																			+1,8
																			-3,5
	+1,85	-0,76		-0,24	-4,65		+0,13	-0,88		-0,17	-0,82		+2,43	+0,56		+1,89	-0,32		+51,2
				-0,24		-0,48	+0,13	-0,88			-0,82	+1,76							-5,1

2. В панели Matrix(Матрица) щелкните на кнопке Matrix or Vector(Матрица или Вектор) и в открывшемся окне впишите число строк и столбцов, которые надо добавить или удалить.

3. Щелкните сначала на кнопке Insert (Вставить) или Delete (Удалить), затем на кнопку ОК.

Чтобы удалить всю матрицу, выделите ее черным цветом и нажмите клавишу Del (для безвозвратного удаления).

Система Mathсad имеет ряд функций и операторов преобразования векторов. Они позволяют преобразовать вектор и выполнять действия над его элементами. При уравнивании мы будем использовать следующие функции и операторы преобразования:

· Транспонирование матрицы (вектора). Вектор образуется путем нажатия соответствующей кнопки панели инструментов Matrix после ввода символа вектора (имени): B 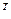=и на экране появится транспонированный массив;

· Создание обратной матрицы. Введите имя матрицы(вектора) и щелкните на кнопке «обращение матриц» меню Matrix: В 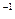=, на экране увидите обращенную матрицу;

· Объединение двух матриц с одинаковым числом строк в одну. Функция augment(M1,M2)образует матрицу больших размеров путем объединения матриц М1 и М2. Объединение происходит путем увеличения числа столбцов.

Объединение двух матриц с одинаковым числом столбцов в одну. Функция stack(M1,M2)образует матрицу больших размеров путем объединения матриц М1 и М2. Объединение происходит путем увеличения числа строк.

Указанные функции объединения матриц используются следующим образом.

1. Наберите имя новой матрицы и оператор присваивания.

2. На стандартной панели инструментов щелкните на кнопке Insert Function (Вставить функцию).

3. В списке функций открывшегося диалогового окна найдите нужную функцию и щелкните на кнопке Insert(Вставить). Имя функции можно набирать и с клавиатуры, но при этом нужно не ошибиться в написании.

4. В места ввода впишите нужные имена массивов.

· Произведение матриц. Оператор умножения в Mathсad по умолчанию обозначается точкой, для ввода которой нужно нажать клавишу < *> (Звездочка) – знак умножения, характерный для языков программирования или значок < · > c панели инструментов Calculator.

Запишем алгоритм уравнивания.

В данной программе существуют ограничения по размерности матриц, максимальная размерность массива 100 элементов, т. е. матрицы размерностью 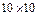. При уравнивании возникает необходимость создать матрицу (табл. 15), размерность которой 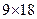. Для того, чтобы описать матрицу заданного формата в Mathсad, воспользуемся искусственным приемом и разделим матрицу на две матрицы В1иВ2, таким образом, чтобы выполнялось обязательное условие: одинаковое количество строк в обеих матрицах, затем выполним операцию по их объединению функцией augment (В1,В2).

B1:=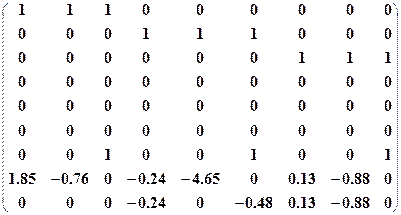

В2:=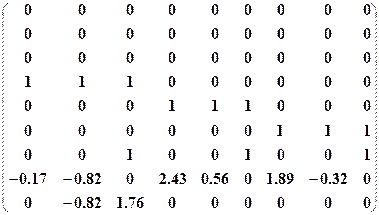

В:= augment (В1,В2)

Проверим, действительно ли мы получили матрицу, соответствующую табл.15.

Для этого введем имя матрицы и знак равенства, затем клавишу <Enter>, на экране должна появиться объединенная матрица Вразмерностью .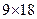

Далее нам необходимо создать единичную матрицу весов, размерность которой 18 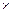18. Создать такую матрицу можно только с помощью объединения нескольких матриц, а в данном случае четырех: Р11, Р22 –единичные матрицы размерностью 9 9, Р12, Р21 –матрицы с нулевыми элементами. Сначала опишем эти матрицы:

Р11:= Р22:=

Р12:= Р21:=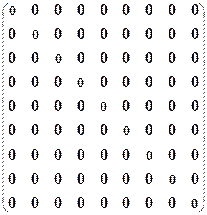

Операцию по объединению будем выполнять в несколько этапов:

1. объединение матриц по строкам функцией augment (Р11,Р12);

2. объединению матриц по строкам функцией augment (Р21, Р22);

3. объединению матриц по столбцам функцией stack(Р1, Р2).

В Mathcad выглядит это следующим образом:

Р1:=augment (Р11,Р12)

Р2:=augment (Р21, Р22)

Р:=stack(Р1, Р2)

В результате мы получили матрицу весов Р. Для проверки введем имя матрицы Р и знак равенства, затем клавишу <Enter>, на экране должна появится объединенная матрица Р, размерностью18 18.

Следующий шаг в нашей работе, описание вектора невязок по известному алгоритму:

W :=

Опишем уравнение коррелат:

К :=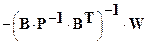

Выведем результат, для этого введем имя вектора коррелат К и знак равенства, затем клавишу <Enter>, на экране появится:

К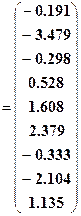

Запишем уравнение вектора поправок:

V :=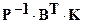

Выведем результат, для этого введем имя вектора поправок V и знак равенства, затем клавишу <Enter>, на экране появится:

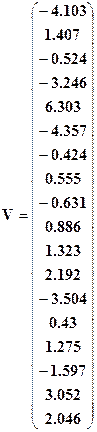
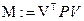
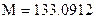
Результатом счета являются значения коррелат (вектор К ), поправки в измеренные углы вектор V и сумма квадратов поправок (M).

Далее полученными поправками исправляют измеренные углы и выполняют окончательное решение треугольников (таблица 13).

Работу заканчивают вычислением координат пунктов сети (таблица 14,15) и оценкой точности уравненных элементов. Работа сдается на проверку в распечатанном виде со всеми промежуточными результатами.

Таблица 13