Неравенства для определенного интеграла Римана и теорема о среднем

Теорема 1:

Если функции 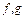интегрируемы на 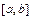и

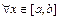
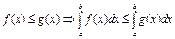
Доказательство:

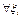выполняется неравенство 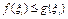, тогда 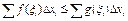. Так как интегралы по условию существуют, по теореме о предельном переходе под знаком неравенства, 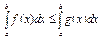. Теорема доказана.

Следствие:

Если 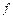- интегрируема на 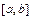, то, по доказанному выше, 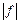- интегрируем на данном отрезке; тогда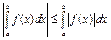

Доказательство:

Известно неравенство: 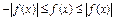; по данной теореме

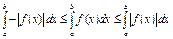; из самого правого интеграла минус можно вынести; получим:

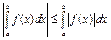. Следствие доказано.

Теорема 2: (о среднем)

Пусть 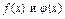интегрируемы на 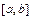, причем 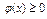на данном промежутке, тогда

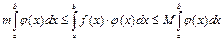, где ,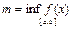

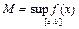
и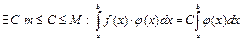

Замечание: sup и inf существуют, т.к. функция на данном промежутке интегрируема, а значит ограничена.

Доказательство:

Запишем неравенство: 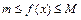и домножим его на :

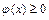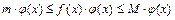; тогда по теореме о неравенствах это неравенство сохранится и в интегралах:

( )

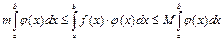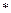Если 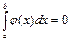, то и интеграл 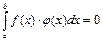и неравенство ( 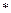) выполняется.

Если 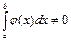, тогда по теореме о неравенствах 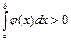, значит можно неравенство ( 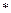) на него разделить:

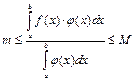и принимаем за 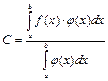. Теорема доказана.

Следствие:

Если 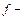непрерывна на 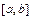и выполняется условие теоремы, то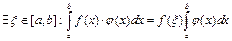

Доказательство:

Т.к. 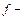непрерывна на 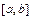, то она достигает своего max и min значения, а в силу непрерывности sup=max, inf=min; значит 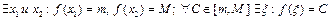- по теореме о промежуточных значениях непрерывной функции. Следствие доказано.

Следствие к следствию:

Если 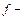непрерывна на 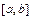, то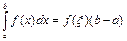

Доказательство:

Возьмем 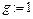, тогда 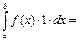(по следствию) 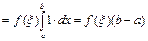. Следствие доказано.

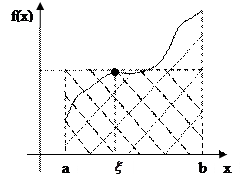Геометрический смысл этого следствия:

Если считать площадь криволинейной трапеции, то найдется такая точка 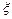, что площадь этой криволинейной трапеции будет равна площади прямоугольника с высотой .

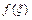Билет 47

Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.

Рассмотрим функцию 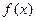, интегрируемую на отрезке 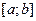. По аддитивному свойству интеграла:

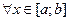, можно найти отрезок 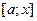на котором представляется возможным рассмотреть функцию .

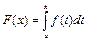Теорема:

Если функция 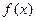интегрируема на отрезке 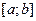, то 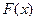непрерывна на отрезке .

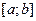Доказательство:

Рассмотрим функцию ,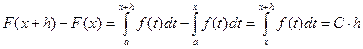

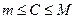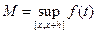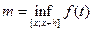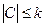, где , , , где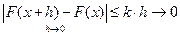

Теорема доказана.

Теорема:

Пусть функция 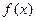интегрируема на отрезке 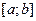, непрерывна в точке 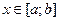, тогда функция 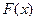дифференцируема в точке 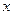и .

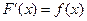Доказательство:

,

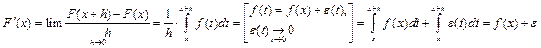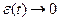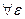
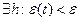
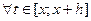, , т.е.

.

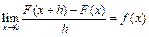Теорема доказана.

Следствие:

Если функция 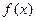непрерывна на отрезке 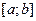, то 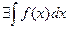, т.е. 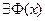- первообразная .

,

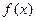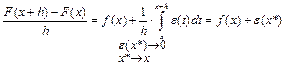Функция 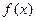непрерывна в точк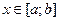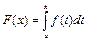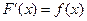е , ; , где 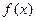непрерывна на отрезке 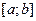. Заключаем, что .

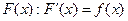Т.е. любая непрерывная функция имеет первообразную.

Теорема доказана.

Формула Ньютона-Лейбница:

Функция 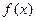непрерывна на отрезке 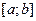, тогда она имеет первообразную. Пусть 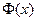- её произвольная первообразная. Тогда .

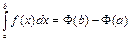Доказательство:

Функция 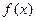непрерывна на отрезке 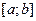, 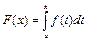- первообразная функции ,

, ,

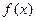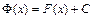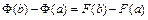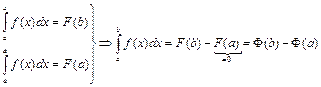. Теорема доказана.

Билет 48