Аддитивное и однородные свойства определенного интеграла Римана
Теорема 1: (Аддитивное свойство интегралов)
Функция 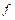 интегрируема на отрезке
интегрируема на отрезке 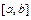 тогда и только тогда, когда
тогда и только тогда, когда 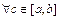 функция интегрируема на отрезках
функция интегрируема на отрезках 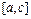 и
и 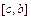 и при этом выполняется равенство:
и при этом выполняется равенство: 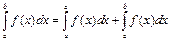
Доказательство:
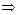 Пусть
Пусть 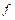 интегрируема на
интегрируема на 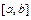 , тогда по основной теореме
, тогда по основной теореме 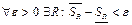
Можно считать, что точка c является точкой разбиения, потому что, если она таковой не является, мы добавим эту точку и рассмотрим новое разбиение 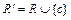 , тогда
, тогда 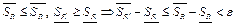 , поэтому можно считать, что разбиение R изначально содержит точку с. Тогда это разбиение порождает разбиения
, поэтому можно считать, что разбиение R изначально содержит точку с. Тогда это разбиение порождает разбиения 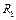 - разбиение
- разбиение 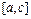 и
и 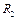 - разбиение
- разбиение 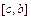 . Тогда
. Тогда 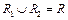 и разность сумм Дарбу можно представить как:
и разность сумм Дарбу можно представить как:
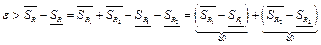 . Так как каждое из этих двух слагаемых неотрицательно и в сумме они меньше
. Так как каждое из этих двух слагаемых неотрицательно и в сумме они меньше 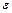 , значит каждое из них меньше
, значит каждое из них меньше 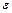
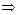 по основной теореме
по основной теореме 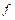 интегрируема на
интегрируема на 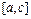 и
и 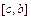 . Доказано.
. Доказано.
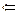 Пусть
Пусть 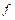 интегрируема на отрезках
интегрируема на отрезках 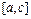 и
и 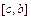 , тогда точно так же найдем
, тогда точно так же найдем 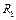 - разбиение
- разбиение 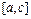 и
и 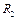 - разбиение
- разбиение 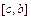 , такие что
, такие что 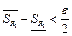 и
и 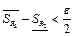 , тогда для разбиения
, тогда для разбиения 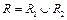
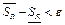 , где R–разбиение отрезка
, где R–разбиение отрезка 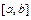 ,
,
значит 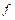 интегрируема на отрезке
интегрируема на отрезке 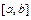 . Доказано.
. Доказано.
Доказали интегрируемость, теперь докажем равенство 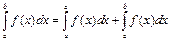 :
:
Замечание: Мы предполагаем, что точка с участвует во всех этих разбиениях; если она в них не участвует, то по следствию из основной теоремы нам это неважно, поскольку если хотя бы для одной последовательности разбиений предел стремится к числу, то и для всех остальных - тоже. И мы берем такую последовательность разбиений, что точка с в них участвует.
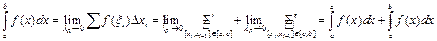
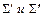 - сумма берется по тем отрезкам, которые содержатся в
- сумма берется по тем отрезкам, которые содержатся в 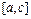 и
и 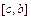 соответственно. Нужно учесть, что
соответственно. Нужно учесть, что 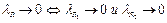 . Теорема доказана.
. Теорема доказана.
Замечание: Мы определили понятие определенного интеграла только для случая 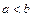 ; доопределим понятие определенного интеграла от a до b в случае, когда
; доопределим понятие определенного интеграла от a до b в случае, когда 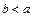 :
:
Если 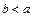 , то положим
, то положим 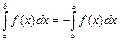 , тогда равенство
, тогда равенство 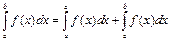 становится верным не только для
становится верным не только для 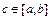 , но и для любых
, но и для любых 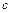 , при условии что все вышеперечисленные интегралы существуют.
, при условии что все вышеперечисленные интегралы существуют.
Пример: 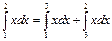
Теорема2: (Однородные свойства интегралов)
Пусть функции 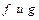 интегрируемы на
интегрируемы на 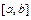 , тогда
, тогда
1) f + g – интегрируема на 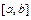 и
и 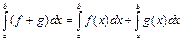 , если интегралы в правой части существуют, т.е. в общем случае обратное не верно.
, если интегралы в правой части существуют, т.е. в общем случае обратное не верно.
(Пример: Если взять f – неинтегрируема на 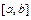 и –f – тоже неинтегрируема, то их сумма =0 – интегрируема).
и –f – тоже неинтегрируема, то их сумма =0 – интегрируема).
2) 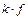 - интегрируема на
- интегрируема на 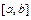 и
и 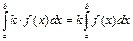 , обратное тоже верно, в случае если
, обратное тоже верно, в случае если 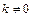
3) 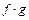 - интегрируема.
- интегрируема.
4) 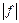 - интегрируем
- интегрируем
5) Если 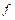 отделена от 0 на отрезке
отделена от 0 на отрезке 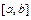 , т.е.
, т.е. 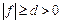 на
на 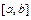 где
где 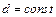 , то
, то 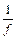 - интегрируема.
- интегрируема.
Доказательство:
1) 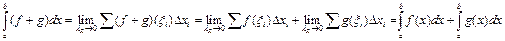
2) аналогично;
Замечание: обозначим 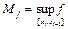 ;
; 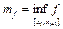 ;
; 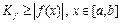 - по свойству ограниченности; соответственно введем
- по свойству ограниченности; соответственно введем 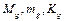
3) 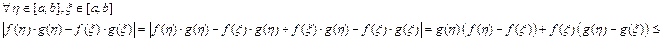
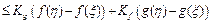
Перейдем к супремумам: на произвольном промежутке 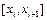
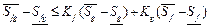
По основной теореме найдутся такие разбиения 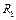 , что
, что 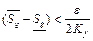 и
и 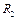 , что
, что 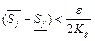 . Теперь если мы возьмем сумму разбиений
. Теперь если мы возьмем сумму разбиений 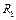 и
и 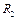 , то будут выполняться оба неравенства, и тогда
, то будут выполняться оба неравенства, и тогда 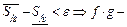 интегрируема.
интегрируема.
4) 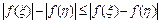 ; переходя к супремумам и умножая на
; переходя к супремумам и умножая на 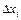 , получим:
, получим:
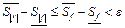
Замечание: переход к супремуму на промежутке 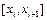 :
: 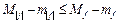
Замечание: обратное неверно:
Контрпример: 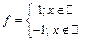 - сама по себе не интегрируема (доказано ранее), а по модулю – интегрируема.
- сама по себе не интегрируема (доказано ранее), а по модулю – интегрируема.
5) 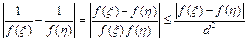 ; переходя к супремумам супремум в этом неравенстве, получим:
; переходя к супремумам супремум в этом неравенстве, получим:
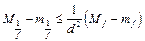 ; теперь домножая на
; теперь домножая на 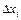 и суммируя, получим
и суммируя, получим
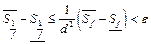
Теорема доказана.
Билет 46
