Использование нейронных сетей для решения задач маршрутизации

Маршрутизация является одной из важных задач для телекоммуника­ционных сетей различного назначения. Задачи, связанные с выбором маршрута, планированием работы средств связи и т. п., относятся к классу сложных комбинаторно-оптимизационных задач, как правило, не имею­щих простых аналитических решений. Кроме того, сложность необходи­мых вычислений экспоненциально возрастает при увеличении количества узлов в сети. Поэтому в настоящее время широко применяют различные эвристические алгоритмы и процедуры, полученные путем творческого поиска, интуиции и опыта исследователя. Альтернативой существующим методам решения задач маршрутизации является использование нейросе­тевых моделей, которые позволяют при значительном снижении времен­ных затрат получить хорошие субоптимальные решения. Так, для реше­ния комбинаторно-оптимизационных задач широко используются модели построенные на основе НС Хопфилда, впервые примененные для решения задачи о коммивояжере. Эти модели явились началом развития нейрон­ных методов решения сложных оптимизационных задач.

Коротко остановимся на формулировке и основных принципах организации вычислений при решении задачи коммивояжера.

Для некоторой группы городов с известными расстояниями между ни­ми требуется найти кратчайший маршрут посещения каждого города один раз с возвращением в исходную точку.

Обозначим города, которые необходимо посетить, буквами А, В, С..., а расстояния – d_AB­, d_AC, и т.д. Решением является упорядоченное множе­ство из n городов. Последовательность, в которой обходятся города удобно представлять матрицей n´n, строки которой соответствуют горо­дам, а столбцы номерам городов в последовательности. Например, имеет­ся пять городов А, В, С, D, Е, а последовательность обхода этих городов задана матрицей

А
В
С
D
Е

Таким образом город С посещается первым, город А - вторым и т. д. Длина маршрута равна d_CA + d_AE + ... + d_DC. В каждом столбце и в каждой строке этой матрицы может быть только одна единица, так как в каждый момент посещается только один город и каждый город посещается только один раз. Матрицу вида (1) можно воспринимать как состояние нейрон­ной сети из N = n² нейронов. Задача состоит в том, чтобы из n!/2n мар­шрутов выбрать один с наименьшей длиной. Состояние каждого нейрона описывается двумя индексами, которые соответствуют городу и порядко­вому номеру его посещения в маршруте. Например, Yx_j=1 показывает, что город х был j-м по порядку городом маршрута.

Запишем функцию вычислительной энергии для сети, предназначен­ной для решения задачи коммивояжера, в которой состояние с наимень­шей энергией соответствует самому короткому маршруту. В общем виде такая функция для рассматриваемой сети может иметь следующий вид:

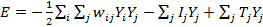(10)

где Е - искусственная энергия сети, w_j - вес от выхода нейрона i к входу нейрона j,

Y_j – выход нейрона j, I_j - внешний вход нейрона j , T_j -порог нейрона j.

Изменение энергии, вызванное изменением состояния j-нейрона, можно вычислить следующим образом:

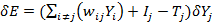(11)

где dY_j - изменение выхода j-го нейрона.

Каждому состоянию системы соответствует конкретная величина вы­числительной энергии. Устойчивое состояние имеет меньшую энергию, чем неустойчивое. Эволюция системы во времени – это движение в про­странстве состояний в поисках минимума энергии и остановка в этой точке.

Для рассматриваемой системы функция энергии должна удовлетворять следующим требованиям. Во-первых, она должна поддерживать ус­тойчивые состояния в форме матрицы (1). Во-вторых, из всех возмож­ных решений функция энергии должна поддерживать те, которые соот­ветствуют коротким маршрутам. Этим требованиям удовлетворяет функция энергии вида

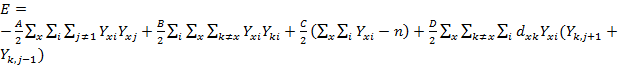(12)

Первые три члена выражения (12) поддерживают первое требование, четвертый член - второе; А, В, С, D - положительные множители. Первый член равен нулю, если каждая строка х содержит не больше одной еди­ницы. Второй член равен нулю, если каждый столбец содержит не более одной единицы. Третий член равен нулю, если в матрице вида (10) n еди­ниц. Таким образом, без учета четвертого члена функция энергии имеет минимумы (Е = 0) во всех состояниях, представленных матрицей с одной единицей в каждом столбце и каждой строке. Все другие состояния имеют более высокую энергию. Короткие маршруты поддерживает четвертый член. В нем индексы i берутся по modn, для того чтобы показать, что i -и город соседствует в маршруте с (n-1) -м и первым, т. е. Y_k,n+j=Y_k,j. Четвертый член численно равен длине маршрута.

Раскрывая скобки в (12) и приравнивая коэффициенты при квадратич­ных и линейных членах в полученном выражении и общей формуле энер­гии, определяем матрицу связей и внешние взаимодействия:

W_xi,kj = –Ad_xk(l-d_ij)–Bd_xk(1-d_xk)–C–Dd_xk(d_j,i+1+d_j,i-1), (13)

где d_ij = 1, если i=j, в противном случае d_xi=0 . Кроме того, каждый нейрон имеет смещающий вес I_xi=С_п .

Первый член в (4) задает связи нейронов в каждой строке, второй -внутри каждого столбца, третий и четвертый - глобальные связи. И в (12) и в (13) три первых члена отвечают за общие ограничения для любой за­дачи коммивояжера и приводят сеть к финальному состоянию в виде (10). Четвертый член управляет тем, какое из n!/2n возможных различных фи­нальных состояний соответствует самому короткому маршруту.