Первообразная. Неопределённый интеграл

Первообразная.Непрерывная функция F ( x ) называется первообразной для функции f ( x ) на промежутке X , если для каждого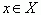

F’ ( x ) = f ( x ).

П р и м е р . Функция F ( x ) = x ³ является первообразной для функции

f ( x ) = 3x ² на интервале ( - 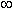, + 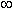) , так как

F’ ( x ) = ( x ³)’ = 3x ² = f ( x ) для всех x 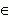( - 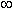, + 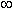) . Легко проверить, что функция x ³ + 13 имеет ту же производную 3x ², поэтому x ³ + 13 также является первообразной для функции 3x ² для всех x 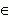( - 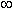, + 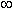) . Ясно, что вместо 13 можно взять любую постоянную.

Таким образом, задача нахождения первообразной имеет бесчисленное множество решений. Этот факт нашёл отражение в определении неопределённого интеграла.

Неопределённый интеграл функции f ( x ) на промежутке X есть множество всех её первообразных. Это записывается в виде:

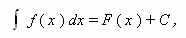
где C – любая постоянная, называемая постоянной интегрирования.

Основные свойства неопределённого интеграла

Если функция f ( x ) имеет первообразную на промежутке X, и k – число, то

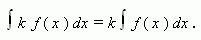
Т.е. постоянную можно выносить за знак интеграла.

Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , то

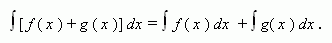
Т.е. интеграл суммы равен сумме интегралов.

Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:

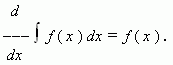
Т.е. производная от интеграла равна подынтегральной функции.

Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:

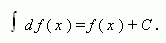
Т.е. интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.

Определённый интеграл. Формула Ньютона – Лейбница

Рассмотрим непрерывную функцию y = f ( x ), заданную на отрезке [ a, b ] и сохраняющую на этом отрезке свой знак ( рис.8 ).
Фигура, ограниченная графиком этой функции, отрезком [ a, b ] и прямыми x = a и x = b, называется криволинейной трапецией.
Для вычисления площадей криволинейных трапеций используется следующая теорема:

Если f – непрерывная, неотрицательная функция на отрезке [a, b], и F – её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a, b], т.e.

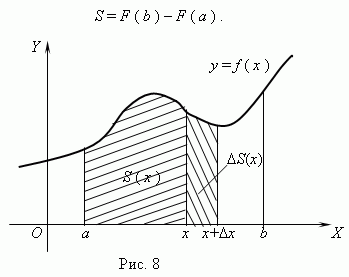
Рассмотрим функцию S ( x ), заданную на отрезке [ a, b ]. Если a<x 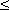b, то S ( x ) – площадь части криволинейной трапеции, лежащей слева от вертикальной прямой, проходящей через точку ( x, 0 ). Отметим, что если x = a , то S ( a ) = 0, а S ( b ) = S ( S – площадь всей криволинейной трапеции). Можно доказать, что

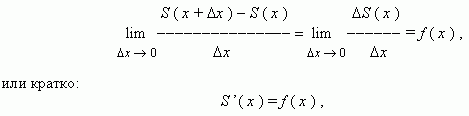
т.e. S ( x ) – первообразная для f ( x ). Отсюда, согласно основному свойству первообразных, для всех x 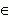[ a, b ] имеем:

S ( x ) = F ( x ) + C ,

где C – некоторая постоянная, F – одна из первообразных функции f .

Чтобы найти C , подставим x = a :

F ( a ) + C = S ( a ) = 0,отсюда, C = -F ( a ) и S ( x ) = F ( x ) - F ( a ). Так как площадь криволинейной трапеции равна S ( b ) , то подставляя x = b , получим:

S = S ( b ) = F ( b ) - F ( a ).