Задачи динамического анализа рычажных механизмов
Конечной целью динамического анализа рычажного механизма является определение реакций в кинематических парах и уравновешивающего (движущего) момента, действующего на кривошипный вал со стороны привода. Указанные задачи решаются методом кинетостатики, основанным на принципе Даламбера. Этот метод предполагает введение в расчет инерционных нагрузок (главных векторов и главных моментов сил инерции), для определения которых требуется знать ускорения центров масс и угловые ускорения звеньев. Поэтому силовому расчету предшествует кинематический анализ механизма по известному уже закону вращения кривошипа (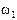 
, 
).
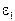Кинематический анализ
Кинематический анализ рычажного механизма производится после того, как в результате динамического анализа машинного агрегата установлен закон движения звена приведения (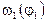 
, 
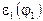). Учитывая, что закон движения кривошипа рычажного механизма такой же, как и звена приведения, при кинематическом анализе требуется определить соответствующие этому закону движения линейные скорости и ускорения отдельных точек, а также угловые скорости и ускорения звеньев механизма.
Известно, что угловая скорость к-го звена равна
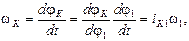
т.е. угловая скорость к-го звена равна произведению аналога угловой скорости этого звена на угловую скорость звена приведения 1.
Аналогичные выражения можно получить для проекций скорости какой-либо точки звена (например, точки М)
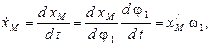
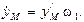
Угловое ускорение к-го звена
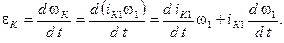
Так как
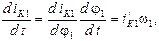
то
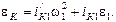
Аналогично рассуждая, получим проекции ускорения точки М:
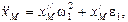
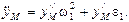
Алгоритм определения скоростей и ускорений для кривошипно-ползунных механизмов (рис. 1.5) имеет вид
1. 
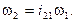
2. 
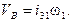
3. 
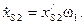
4. 
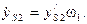
5. 
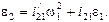
6. 
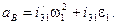
7. 
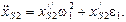
8. 
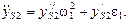
Модули и направления векторов абсолютной скорости и ускорения точки S2 определяются на основании выражений:
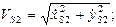
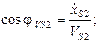
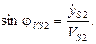
Силовой расчет
При силовом расчете механизма рассматриваются статически определимые кинематические цепи (группы Ассура), причем расчет начинается с группы, наиболее удаленной от начального звена.
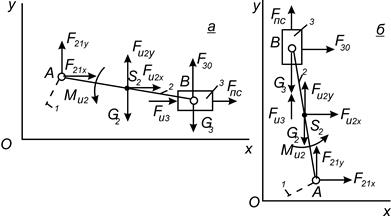
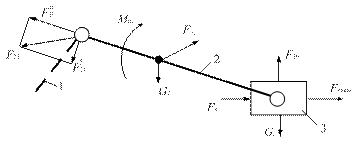
Расчетные схемы группы Ассура 2-го вида показаны на рис 2.1.
- переделать в аналитику!!
Рис. 2.1
К звеньям (2,3) группы приложим внешнюю нагрузку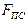 
, силы тяжести звеньев G2, G3. Реакцию 
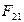во вращательной кинематической паре А представим в виде проекци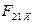й 
и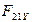 
. Реакция 
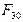в поступательной кинематической паре В перпендикулярна направлению перемещения ползуна и в данном случае проходит через точку В.
В соответствии с принципом Даламбера приложим к звеньям (2,3) инерционные нагрузки.
Проекции главного вектора сил инерции звена 2
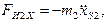
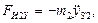
главный момент сил инерции звена 2
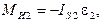
главный вектор сил инерции звена 3
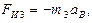
Силы тяжести звеньев равны
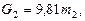
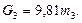
Реакции в кинематических парах группы с горизонтально расположенным ползуном вычисляются в следующей последовательности (рис. 2.1.а).
1. Из условия, что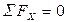 
, определятся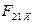
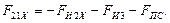
2. Реакция 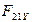определяется из уравнения равновесия моментов сил для звена 2 относительно точки В
,
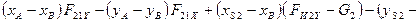
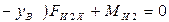откуда
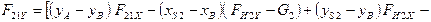
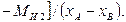
3. Реакция 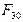определяется из условия равновесия проекций сил, действующих на группу (2,3), на ось Y, т.е.
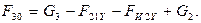
Для определения проекци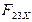й 
и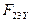 
реакции во внутренней кинематической паре В рассмотрим равновесие звена 2 под действием приложенных сил:
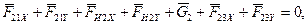
откуда, проектируя на оси координат, получим
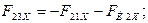
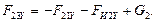
Модули реакци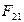й и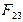 
определяем как
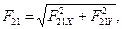
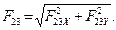
Направление реакци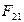й и 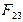установим, определив углы наклона их к оси Х:
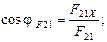
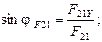
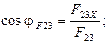
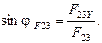
Реакции в кинематических парах группы (2,3) с вертикальным расположением ползуна (рис. 2.1, б) вычисляются в следующей последовательности:
1. Из условия, что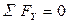 
, определяется :
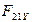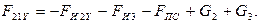
2. Реакция 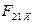определяется из уравнения равновесия моментов сил для звена 2 относительно точки В:
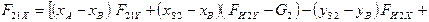
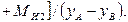
3. Реакция 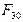определяется из условия равновесия проекций сил, действующих на группу (2,3), на ось Х:
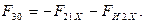
Определение реакци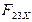й и 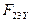, их модулей и направлений осуществляется по тем же формулам, что и для группы с горизонтальным расположением ползуна.
 |
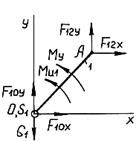Далее рассматривается кривошип 1 (рис. 2.2).
Рис. 2.2
В точке А приложена известная реакция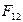 
, проекции которой равны
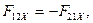
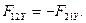
В точке О расположена сила тяжести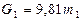 
и неизвестная реакция 
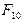. Кроме того, к звену приложен известный главный момент сил инерции
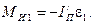
Для того, чтобы звено 1 двигалось по заданному закону, к нему приложен уравновешивающий момент сил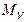 
, который является реактивным моментом со стороны отсоединенной части машины. Его величина определяется из уравнения моментов сил относительно точки О:
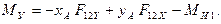
Реакция 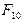в проекциях имеет вид:
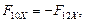
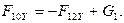
Модуль
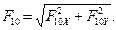
Направление 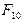определяется углом 
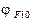по
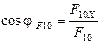и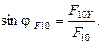 
На основании вышеизложенного можно представить алгоритм силового расчета кривошипно-ползунных механизмов:
1. 
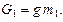
2. 
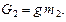
3. 
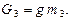
4. 
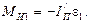
5. 
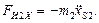
6. 
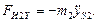
7. 
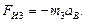
8. 
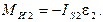
При горизонтальном расположении ползуна:
9. 
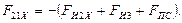
10. 
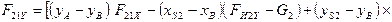
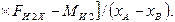
11. 
При вертикальном расположении ползуна:
9. 
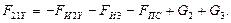
10. 
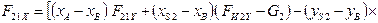
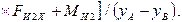
11. 
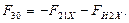
Далее для обеих схем:
12. 
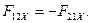
13.
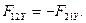
14. 
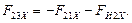
15.
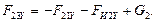
16. 
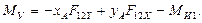
17. 
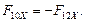
18. 
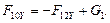
19.
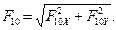
20. 
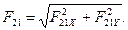
21. 
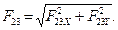
Таблица 2.1
| № | Параметр | Условное обозначение | Единица измерений | Величина |
| Схема кривошипно- ползунного механизма | - | - | ||
| Размеры звеньев | 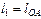 | м | ||
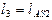 | м | |||
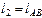 | м | |||
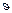 | м | |||
| Начальная обобщенная координата | 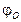 | град | ||
| Массы и моменты инерции звеньев | 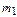 | кг | ||
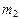 | кг | |||
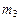 | кг | |||
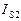 | кг м2 | |||
| Постоянная составляющая приведенного момента инерции | 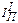 | кг м2 |
Таблица 2.2
| № положения кривошипа | Угловая скорость 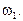 , с-1 | Угловое ускорение 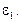 , с-2 | Сила полезного сопротивления FПС,, H |
ВЫВОД
Результаты определения реакций в кинематических парах дают возможность выполнять прочностные расчеты звеньев, правильно подойти к конструктивному оформлению подвижных соединений (выбор подшипников, условий смазки и т.д.), количественно оценить трение и износ, а также коэффициенты полезного действия.