Теорема Ролля. Теорема Лагранжа.

Теорема Ролля:

Если функция y = f(x) удовлетворяет следующим условиям:

· Непрерывна на отрезке: f(x) принадл. C[a;b]

· Дифференцируема на интервале: f(x) принадл. D`(a;b)

· Значения на концах промежутков равны: f(а) = f(b)

тогда найдется хотя бы одна точка, £ принадлежащая (a;b), такая что f`(£) = 0

Теорема Лагранжа:

Пусть функция y = f(x) удовлетворяет условиям:

· f(x) принадл. C[a;b]

· f(x) принадл. D`(a;b)

тогда найдется хотя бы одна точка £ принадл. (a;b) такая что:

f`(£) =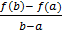

Найдется хотя бы 1 точка, в которой касательная, проведенная к графику будет || к хорде , п

Вопрос №25
Теорема Коши (с доказательством)

Теорема:Пусть функция y = f(x) удовлетворяет след.условиям:

· f(x) принадл. C[a;b]

· f(x) принадл. D`(a;b)

а так же существует функция g(x), которой удовлетвор. тем же условиям, а так же её производная ≠0 . тогда существует точка £ из промежутка (a;b) такая, что:

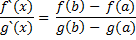
Док-во:
F(x) = f(x) - 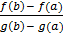(g(x) – g(a))

Проверим, выполняются ли условия для новой функции:

1. F(x) непрерывна на отрезке [a;b] по 1-му условию данной теоремы;

2. F(x) принадл. D`(a;b) по 2-му условию

3. F(a) = 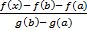( g(a) – g(a) )

F(a) = f(a)

F(b) = f(b) = 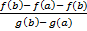( g(b) – g(b))

F(b) = f(a)

По теореме Ролля найдем хотя бы 1 точку, где F`(x) = 0:

F`(£) = 0

F`(x) = f`(x) =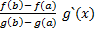

F`(£) =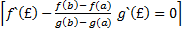

F`( =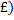

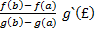
Поделив обе части на нулевую производную g в точке £ получаем доказываемое равенство.

Правило Лопиталя:

Предел отношения двух бмв или ббв равно приделу отношения их производных, если последний существует:

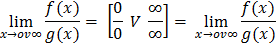
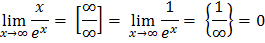
Вопрос №?

Выпуклость функции вверх Точки перегиба функции. Необходимые и достаточные условия перегиба функции.

Направления выпуклости. Кривая называется выпуклой вверхна промежутке если для двух любых других точек этого промежутка с абсциссами из этого промежутка, соединяющая их хорда всеми своими точками лежит ниже кривой.

1. Кривая выпукла вверхна заданном промежутке тогда и только тогда, когда её первая производная на этом промежутке монотонно убывает(возрастает)

Теорема: если вторая производная дважды дифференцируемой функции положительна(отрицательна) внутри заданного пром-ка, то фун-я выпукло вверх(вниз)

Точка перегибаграфика непрерывной функции называется точка, которая разделяет интервалы выпуклости вверх и вниз.

Теорема 1. Необходимое условие перегиба:

Вторая производная дважды дифференцируемой функции в точке перегиба = 0.

Теорема 2. Достаточное условие перегиба:

Если вторая производная дважды дифферен. функции при переходе через точку х₀ меняет свой знак, то эта точка - точка перегиба.

Вопрос №28