Составление таблиц истинности

Примеры из ЕГЭ

1. Докажите равносильность следующих выражений:

А и не (не В или С)

А и В и не С

Запишите логические выражения известными вам способами.

Решение

Чтобы начертить таблицы истинности, выполним следующие действия:

1. Подсчитаем количество строк для трех простых высказываний. В наших выражениях три логических переменных А, В, С; n=3. Количество строк считается по формуле 2ⁿ и прибавляется еще одна строка с наименованиями, т.е. 2³ =8 (строк) и плюс 1. В общем нам необходимо составлять таблицу с девятью строками.

2. Количество столбцов равно количеству переменных плюс количество логических операций: в первом логическом выражении логических операций 4, во втором – 3. Количество столбцов в первом логическом выражении: 3+4=7, во втором – 3+3=6

3. Строим таблицы.

Числа в 10-й СС	Числа в 2-й СС	Логические операции (1 – истина, 0 – ложь)
	А	В	С	не В	не В или С	не(не В или С)	А и не (не В или С)

Для наглядности. В таблицах не пишется

Задание группы В6

Решение логических задач методом рассуждений.

Определите максимальное число учеников, сдавших экзамен при условии, что:

1) Если первый сдал, то и второй сдал.

2) Если второй сдал, то третий сдал или первый не сдал.

3) Если четвертый не сдал, то первый сдал, а третий не сдал.

4) Если четвертый сдал, то и первый сдал.

Ответ: 4

(Слайды 28, 29, 30)

Пример 8 (В10) на решение отводится 4 мин.

Тема задания: «Составление запросов для поисковых систем с использованием логических выражений»

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

1) принтеры & сканеры & продажа

2) принтеры & продажа

3) принтеры | продажа

4) принтеры | сканеры | продажа

Решение: вариант 1 – рассуждение.

1. Меньше всего результатов выдаст запрос с наибольшими ограничениями – первый (нужны одновременно принтеры, сканеры и продажа)

2. На втором месте – второй запрос (одновременно принтеры и сканеры)

3. Далее – третий запрос (принтеры или сканеры)

4. Четвертый запрос дает наибольшее количество результатов (принтеры или сканеры или продажа)

Таким образом, верный ответ – 1234

Вариант 2 - через диаграммы.

1. Запишем все ответы через логические операции

Х1 = А*В*С Х2 = А*В Х3 = А+В Х4 = А+В+С

2. Покажем области, определяемые этими выражениями, на диаграмме с тремя областями

Х1 Х2 Х3 Х4

Таким образом, верный ответ – 1234

(Слайды 31,32)

Пример 10 (В4) – на решение отводится 10 мин.повышенный уровень.

Тип заданий на тему «Преобразование логических выражений»

А, В, С – целые числа, для которых истинно высказывание:

((С > A) Ú (B < A) Ù ( (B+1<C) Ú A>C – 8)

Чему равно максимально возможное С, если А =16, В = 22

Решение:

Подставим А и В в исходное выражение:

((С > 16) Ú (22 < 16)) Ù ( (22+1< C) Ú 16 > C – 8)

Имеем 22 < 16 – ложно, получим выражение:

(С > 16) Ù ( (23 < C) Ú 16 > C – 8)

Преобразовав его получим: (С > 16) Ù ((23 ≥ C) Ú 24 > C)

Из полученной системы видно что С=23

(Слайд 33)

Для проверки усвоения материала учащимся предлагается самостоятельная работа из 3 заданий на 10 минут.

Приложение 1

Карточки

(Слайд 34)

1 вариант

1. Укажите, какое логическое выражение равносильно выражению (A Ú B Ú C) ?

1) A Ú B Ú C2) A Ù B Ù C

3) A Ú B Ú C4) A Ù B Ù C

2. В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

А) реферат | математика | Гаусс

Б) реферат | математика | Гаусс | метод

В) реферат | математика

Г) реферат & математика & Гаусс

3. На одной улице стоят в ряд 4 дома, в каждом из них живет по одному человеку. Их зовут Алексей, Егор, Виктор и Михаил. Известно, что все они имеют разные профессии: рыбак, пчеловод, фермер и ветеринар. Известно, что

(1) Фермер живет правее пчеловода.

(2) Рыбак живет правее фермера.

(3) Ветеринар живет рядом с рыбаком.

(4) Рыбак живет через дом от пчеловода.

(5) Алексей живет правее фермера.

(6) Виктор – не пчеловод.

(7) Егор живет рядом с рыбаком.

(8) Виктор живет правее Алексея.

2) В стене имеется прямоугольное отверстие с длинами сто­рон X и Y. При каком условии труба, сечением которой являет­ся круг радиуса R, пройдет в это отверстие, если длина трубы превышает X + Y?

1) (3,14*R*R < X*Y) и (R < X+Y)

2) (2*R <= X) или (2*R <= Y)

3) (2*R <= X+Y) или (R <= Y)

4) (X >= 2*R) и (Y >= 2*R)

3) При каком условии последовательность числовых пере­менных А, В и С не является упорядоченной по возрастанию?

1) (А<В) и (не(В>=С)) 3) (В>А) и (не(В>=С))

2) не ((В<=А) или (В>=С)) 4) не ((А<=В) и (В<=С))

Используя таблицу на стр. 35, записать в тетради результаты на языке программирования и на языке логики.

Порядок действий в алгебре логики:

1. Отрицание (инверсия).

2. Умножение (конъюнкция).

3. Сложение (дизъюнкция).

II. Новый материал

Дано высказывание (А или В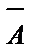) и ( или ).

1. Перепишите в тетради данную формулу тремя способами, используя: а) арифметические знаки; б) специальные знаки; в) язык программирования.

2. Составьте таблицу истинности, для этого используйте алгоритм:

Последовательность действий для составления таблиц истинности:

1) Определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение.

Если количество логических переменных n, то количество строк равно 2ⁿ.

Для случая в упражнении 1 логическая формула имеет две переменные, тогда количество строк равно 2² = 4.

2) Определить количество столбцов, которое равно количеству логических переменных плюс количество логических операций.

Для случая в упражнении 1: количество переменных – 2, количество логических операций – 5, тогда количество столбцов – 7.

3) Построить таблицу истинности с определенным нами количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных.

Для случая в упражнении 1 получается следующая таблица истинности:

А	В	А + В		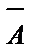	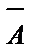+	(А + В) * ( + )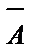

4) Необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.

Задание 1. Начертите таблицу в тетради и заполните ее.

2. Равносильные логические выражения

Какие два уравнения в математике называются равносильными?

2. Логическое сложение (дизъюнкция).

Форма записи дизъюнкции: А или В, А+В, АV В.

В программировании дизъюнкция обозначается А or В.

Соединение двух высказываний А и В в одно с помощью союза «или», потребляемого в неисключающем смысле, называется логическим сложением, а новое составное высказывание – логической суммой.

Таблица истинности дизъюнкции:	А	В	А+В

Задание 2. Составьте дизъюнкцию высказываний А и В и определите ее истинность или ложность.