Оценка устойчивости по критерию Гурвица
ВСЕМИРНЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Филиал в г.Оренбурге
 |
ОТЧЕТ
по расчетно-графической работе
по курсу «Моделирование систем»
Исследование линейной системы управления
ВТУ 220200.62 6 0 11.16 О
Руководитель
___________________ Москалёва О.Г.
“___”___________________2011 г.
Исполнитель
студент гр. БСАУ-ФО-309
__________________Лукашёв А.Н.
“ “ 2011 г.
Оренбург 2011
Содержание
| Введение........................................................................................................ | |
| 1 Цель работы.............................................................................................. | |
| 2 Задание на выполнение РГР…………………………………………… | |
| 3 Оценка устойчивости по критерию Гурвица ........................................ | |
| 4 Оценка устойчивости по критерию Михайлова................................... | |
| 5 Построение областей устойчивости...................................................... | |
| 6 Практическая часть……………………….............................................. | |
| 6.1 Моделирование в системе МВТУ....................................................... | |
| 6.2 Оценка устойчивости по кривой переходного процесса................... | |
| Заключение…............................................................................................... | |
| Список используемой литературы……..................................................... | |
Введение
Развитие техники и технологий в современном обществе способствует формированию и получению новых знаний, которое должно базироваться на методологии системного подхода, в рамках которого особое место занимает модельный подход. Возможности модельного подхода многообразны как по используемым моделям, так и по способам реализации методов моделирования. Физическое моделирование позволяет получить достоверные результаты для достаточно простых систем. Появление новейших информационных технологий увеличивает возможности моделирующих систем, но и позволяет применять большее многообразие моделей и способов их реализации. Совершенствование вычислительной и телекоммуникационной техники привело к дальнейшему развитию методов машинного моделирования, без которых невозможно изучение процессов и явлений, а также построение больших и сложных систем.
Программный комплекс "Моделирование в технических устройствах" ("МВТУ") - современная среда интеллектуального САПР, предназначенная для детального исследования и анализа динамических процессов в ядерных и тепловых энергетических установках, в системах автоматического управления (САУ), в следящих приводах и роботах, в любых технических системах, описание динамики которых может быть реализовано методами структурного моделирования. Может использоваться для моделирования нестационарных процессов в физике, в электротехнике, в динамике машин и механизмов, в астрономии и т.д., а также для решения нестационарных краевых задач (теплопроводность, гидродинамика и др). МВТУ может работать в многокомпьютерных моделирующих комплексах, в том числе и в режиме удаленного доступа к технологическим и информационным ресурсам.
Цель работы
Целью расчетно-графической работы является анализ устойчивости и оценка качества модели линейной системы управления. Модель задается структурной схемой и передаточными функциями отдельных функциональных элементов.
В расчетно-графическом задании необходимо: определить устойчивость системы по различным критериям; построить область устойчивости по коэффициенту усиления системы методом Д - разбиения; провести моделирование системы с помощью программного средства МВТУ; по полученной переходной функции оценить устойчивость системы; в случае устойчивой системы, определить показатели качества системы в установившемся и переходном режимах; построить логарифмические частотные характеристики; оценить по ним устойчивость системы; определить запасы устойчивости по амплитуде и фазе; построить амплитудно-фазовую характеристику, по критерию Найквиста оценить устойчивость, в случае устойчивой системы определить запасы устойчивости по амплитуде и фазе; построить переходной процесс при критическом значении коэффициента усиления.
Задание на выполнение РГЗ
Линейная система управления состоит из следующих функциональных элементов: объект управления ОУ, датчик Д, задающее устройство ЗУ, сравнивающий элемент СЭ, усилитель У, исполнительное устройство ИУ. Система работает по принципу управления по отклонению. Функциональная схема системы приведена на рисунке 1.
 |
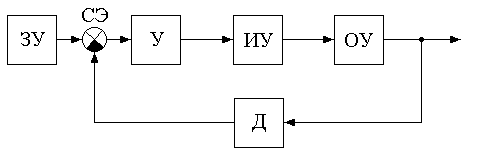Рисунок 1 – 
Функциональная схема линейной системы управления
Элементы системы имеют следующие передаточные функции:
; 
; 
; 
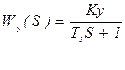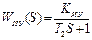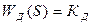
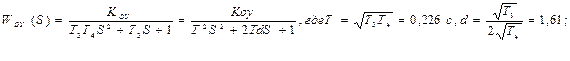Числовые значения коэффициентов усиления и постоянных времени варианта №16 приведены в таблице 1.
Таблица 1 - Числовые значения параметров системы управления
| KД | KОУ | KИУ | KУ | T1, с | T2, с | T3, с | T4, с |
| 0,15 | 0,55 | 0,5 | 0,66 | 0,2 | 0,73 | 0,07 |
Передаточные функции элементов системы управления варианта №16 имеют вид:
; 
; 
= 
;
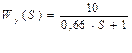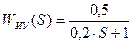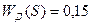
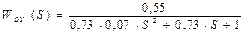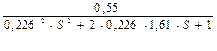В расчетно-графическом задании необходимо:
- определить устойчивость системы по критерию Гурвица;
- определить устойчивость системы по критерию Михайлова;
- построить область устойчивости по коэффициенту усиления системы методом Д-разбиения;
- провести моделирование системы с помощью программного средства МВТУ;
- по полученной переходной функции оценить устойчивость системы;
- определить показатели качества системы в установившемся и переходном режимах;
- построить логарифмические частотные характеристики; оценить по ним устойчивость системы; определить запасы устойчивости по амплитуде и фазе;
- построить амплитудно-фазовую характеристику, по критерию Найквиста оценить устойчивость, определить запасы устойчивости по амплитуде и фазе;
- построить переходной процесс при критическом значении коэффициента усиления У (Усилителя).
Ку = ккр/(коу* киу* кд), где ккр – критическое значение коэффициента усиления системы, найденное методом Д-разбиения.
Оценка устойчивости по критерию Гурвица
Согласно определения критерия Гурвица: система устойчива, если определитель характеристического уравнения передаточной функции, составленный по закону Гурвица положителен, и положительны все его диагональные миноры.
Для нахождения характеристического уравнения находим передаточную функцию всей системы. Для этого находим передаточную функцию системы в разомкнутом состоянии. Так как элементы разомкнутой системы соединены последовательно, то WРАЗ(s) равна произведению передаточных функций элементов:
;
;
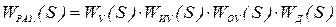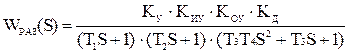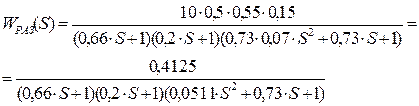
Передаточная функция системы в замкнутом состоянии:
;
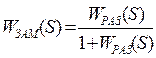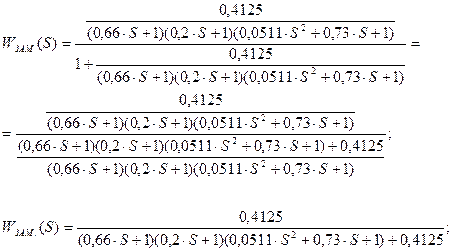
Характеристическое уравнение передаточной функции:
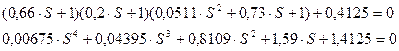
Cоставляем определитель по правилу Гурвица:
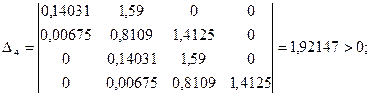
минор 3-го порядка имеет вид:
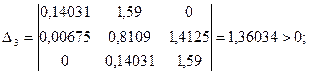
минор 2-го порядка имеет вид:
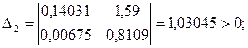
минор 1-го порядка имеет вид:
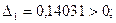
Определитель Гурвица и все его диагональные миноры положительны. Можно сделать вывод, что система устойчива.